Глава 10. Другие формы обучения
10.1 Обучение метрики
Я упоминал, что наиболее часто используемыми метриками сходства (или несходства) между двумя векторами признаков являются евклидово расстояние (Euclidean distance) и косинусное сходство (cosine similarity). Такой выбор метрики кажется логичным, но произвольным, точно так же, как выбор квадрата ошибки в линейной регрессии (или самой формы линейной регрессии). Тот факт, что одна метрика может работать лучше другой в зависимости от набора данных, является индикатором того, что ни одна из них не идеальна.
Вы можете создать метрику, которая работала бы лучше для вашего набора данных. Затем возможно интегрировать вашу метрику в любой алгоритм обучения, который нуждается в метрике, например, k-средних или kNN. Как вы можете узнать, не перебирая все возможности, какое уравнение было бы хорошей метрикой? Как вы уже могли догадаться, метрику можно изучить (learned) из данных.
Вспомним евклидово расстояние между двумя векторами признаков \(\mathbf{x}\) и \(\mathbf{x}'\):
\[ d(\mathbf{x}, \mathbf{x}') = \|\mathbf{x} - \mathbf{x}'\| \stackrel{\text{def}}{=} \sqrt{(\mathbf{x} - \mathbf{x}')^2} = \sqrt{(\mathbf{x} - \mathbf{x}')^\top(\mathbf{x} - \mathbf{x}')}. \]Мы можем немного изменить эту метрику, чтобы сделать ее параметризуемой, а затем изучить эти параметры из данных. Рассмотрим следующую модификацию:
\[ d_A(\mathbf{x}, \mathbf{x}') = \|\mathbf{x} - \mathbf{x}'\|_A \stackrel{\text{def}}{=} \sqrt{(\mathbf{x} - \mathbf{x}')^\top \mathbf{A} (\mathbf{x} - \mathbf{x}')}, \]где \(\mathbf{A}\) — матрица \(D \times D\). Допустим, \(D = 3\). Если мы возьмем \(\mathbf{A}\) как единичную матрицу,
\[ \mathbf{A} \stackrel{\text{def}}{=} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, \]то \(d_A\) становится евклидовым расстоянием. Если у нас есть общая диагональная матрица, например:
\[ \mathbf{A} \stackrel{\text{def}}{=} \begin{pmatrix} 2 & 0 & 0 \\ 0 & 8 & 0 \\ 0 & 0 & 1 \end{pmatrix}, \]то разные измерения имеют разную важность в метрике. (В приведенном выше примере второе измерение является наиболее важным при вычислении метрики.) В более общем случае, чтобы называться метрикой (metric), функция двух переменных должна удовлетворять трем условиям:
- \(d(\mathbf{x}, \mathbf{x}') \ge 0\) неотрицательность,
- \(d(\mathbf{x}, \mathbf{x}') \le d(\mathbf{x}, \mathbf{z}) + d(\mathbf{z}, \mathbf{x}')\) неравенство треугольника,
- \(d(\mathbf{x}, \mathbf{x}') = d(\mathbf{x}', \mathbf{x})\) симметрия.
Чтобы удовлетворить первые два условия, матрица \(\mathbf{A}\) должна быть положительно полуопределенной (positive semidefinite). Положительно полуопределенную матрицу можно рассматривать как обобщение понятия неотрицательного вещественного числа на матрицы. Любая положительно полуопределенная матрица \(\mathbf{M}\) удовлетворяет:
\[ \mathbf{z}^\top \mathbf{M} \mathbf{z} \ge 0, \]для любого вектора \(\mathbf{z}\), имеющего ту же размерность, что и количество строк и столбцов в \(\mathbf{M}\).
Приведенное выше свойство следует из определения положительно полуопределенной матрицы. Доказательство того, что второе условие выполняется, когда матрица \(\mathbf{A}\) положительно полуопределена, можно найти на сопутствующем веб-сайте книги.
Чтобы удовлетворить третье условие, мы можем просто взять \((d(\mathbf{x}, \mathbf{x}') + d(\mathbf{x}', \mathbf{x}))/2\).
Допустим, у нас есть неаннотированный набор \(\mathcal{X} = \{\mathbf{x}_i\}_{i=1}^N\). Чтобы построить обучающие данные для нашей задачи обучения метрики, мы вручную создаем два набора. Первый набор \(\mathcal{S}\) таков, что пара примеров \((\mathbf{x}_i, \mathbf{x}_k)\) принадлежит набору \(\mathcal{S}\), если \(\mathbf{x}_i\) и \(\mathbf{x}_k\) похожи (с нашей субъективной точки зрения). Второй набор \(\mathcal{D}\) таков, что пара примеров \((\mathbf{x}_i, \mathbf{x}_k)\) принадлежит набору \(\mathcal{D}\), если \(\mathbf{x}_i\) и \(\mathbf{x}_k\) непохожи.
Чтобы обучить матрицу параметров \(\mathbf{A}\) из данных, мы хотим найти положительно полуопределенную матрицу \(\mathbf{A}\), которая решает следующую задачу оптимизации:
\[ \min_{\mathbf{A}} \sum_{(\mathbf{x}_i, \mathbf{x}_k) \in \mathcal{S}} \|\mathbf{x} - \mathbf{x}'\|_A^2 \quad \text{при условии } \sum_{(\mathbf{x}_i, \mathbf{x}_k) \in \mathcal{D}} \|\mathbf{x} - \mathbf{x}'\|_A \ge c, \]где \(c\) — положительная константа (может быть любым числом).
Решение этой задачи оптимизации находится градиентным спуском с модификацией, которая гарантирует, что найденная матрица \(\mathbf{A}\) является положительно полуопределенной. Мы оставляем описание алгоритма за рамками этой книги для дальнейшего чтения.
Следует отметить, что обучение с одного примера (one-shot learning) с сиамскими сетями (siamese networks) и тройной потерей (triplet loss) можно рассматривать как задачу обучения метрики: пары изображений одного и того же человека принадлежат множеству \(\mathcal{S}\), в то время как пары случайных изображений принадлежат \(\mathcal{D}\).
Существует много других способов изучения метрики, включая нелинейные и основанные на ядрах. Однако тот, который представлен в этой книге, а также адаптация обучения с одного примера, должны быть достаточными для большинства практических приложений.
10.2 Обучение ранжированию
Обучение ранжированию (Learning to rank) — это задача обучения с учителем. Среди прочего, одна из частых проблем, решаемых с помощью обучения ранжированию, — это оптимизация результатов поиска, возвращаемых поисковой системой
по запросу. При оптимизации ранжирования результатов поиска размеченный пример \(\mathbf{X}_i\) в обучающем наборе размера \(N\) представляет собой ранжированную коллекцию документов размера \(r_i\) (метки — это ранги документов). Вектор признаков представляет каждый документ в коллекции. Цель обучения — найти функцию ранжирования (ranking function) \(f\), которая выводит значения, которые можно использовать для ранжирования документов. Для каждого обучающего примера идеальная функция \(f\) выводила бы значения, которые индуцируют то же ранжирование документов, что и заданное метками.
Каждый пример \(\mathbf{X}_i\), \(i = 1, \dots, N\), представляет собой коллекцию векторов признаков с метками: \(\mathbf{X}_i = \{(\mathbf{x}_{i,j}, y_{i,j})\}_{j=1}^{r_i}\). Признаки в векторе признаков \(\mathbf{x}_{i,j}\) представляют документ \(j = 1, \dots, r_i\). Например, \(x_{i,j}^{(1)}\) может представлять, насколько свежим является документ, \(x_{i,j}^{(2)}\) отражал бы, можно ли найти слова запроса в заголовке документа, \(x_{i,j}^{(3)}\) мог бы представлять размер документа и так далее. Метка \(y_{i,j}\) может быть рангом (\(1, 2, \dots, r_i\)) или оценкой. Например, чем ниже оценка, тем выше должен быть ранжирован документ.
Существует три подхода к решению этой проблемы: поточечный (pointwise), попарный (pairwise) и посписочный (listwise).
Поточечный подход преобразует каждый обучающий пример в несколько примеров: по одному примеру на документ. Задача обучения становится стандартной задачей обучения с учителем, либо регрессией, либо логистической регрессией. В каждом примере \((\mathbf{x}, y)\) поточечной задачи обучения \(\mathbf{x}\) — это вектор признаков некоторого документа, а \(y\) — исходная оценка (если \(y_{i,j}\) — оценка) или синтетическая оценка, полученная из ранжирования (чем выше ранг, тем ниже синтетическая оценка). В этом случае можно использовать любой алгоритм обучения с учителем. Решение обычно далеко от идеального. В основном это связано с тем, что каждый документ рассматривается изолированно, в то время как исходное ранжирование (заданное метками \(y_{i,j}\) исходного обучающего набора) могло оптимизировать позиции всего набора документов. Например, если мы уже присвоили высокий ранг странице Википедии в некоторой коллекции документов, мы предпочли бы не присваивать высокий ранг другой странице Википедии по тому же запросу.
В попарном подходе мы также рассматриваем документы изолированно, но на этот раз рассматривается пара документов одновременно. Для пары документов \((\mathbf{x}_i, \mathbf{x}_k)\) мы строим модель \(f\), которая, получив \((\mathbf{x}_i, \mathbf{x}_k)\) на вход, выводит значение, близкое к 1, если \(\mathbf{x}_i\) должен быть ранжирован выше \(\mathbf{x}_k\) в ранжировании; в противном случае \(f\) выводит значение, близкое к 0. Во время тестирования окончательное ранжирование для неразмеченного примера \(\mathbf{X}\) получается путем агрегирования предсказаний для всех пар документов в \(\mathbf{X}\). Попарный подход работает лучше, чем поточечный, но все еще далек от идеала.
Современные алгоритмы обучения ранжированию, такие как LambdaMART, реализуют посписочный подход. В посписочном подходе мы пытаемся оптимизировать модель непосредственно по некоторой метрике, отражающей качество ранжирования. Существуют различные метрики для оценки ранжирования результатов поисковой системы, включая точность и полноту. Одна популярная метрика, которая сочетает в себе и точность, и полноту, называется средней средней точностью (mean average precision - MAP).
Чтобы определить MAP, попросим судей (Google называет этих людей ранжировщиками) изучить коллекцию результатов поиска по запросу и присвоить метки релевантности каждому результату поиска. Метки могут быть бинарными (1 для «релевантного» и 0 для «нерелевантного») или по некоторой шкале, скажем, от 1 до 5: чем выше значение, тем более релевантен документ поисковому запросу. Пусть наши судьи построят такую разметку релевантности для коллекции из 100 запросов. Теперь протестируем нашу модель ранжирования на
этой коллекции. Точность (precision) нашей модели для некоторого запроса задается:
\[ \text{precision} = \frac{|\{\text{релевантные документы}\} \cap \{\text{возвращенные документы}\}|}{|\{\text{возвращенные документы}\}|}, \]где обозначение \(|\cdot|\) означает «количество». Метрика средней точности (average precision), AveP, определяется для ранжированной коллекции документов, возвращаемых поисковой системой по запросу \(q\), как,
\[ \text{AveP}(q) = \frac{\sum_{k=1}^n (P(k) \cdot \text{rel}(k))}{|\{\text{релевантные документы}\}|}, \]где \(n\) — количество возвращенных документов, \(P(k)\) обозначает точность, вычисленную для топ-\(k\) результатов поиска, возвращенных нашей моделью ранжирования по запросу, \(\text{rel}(k)\) — индикаторная функция, равная 1, если элемент на ранге \(k\) является релевантным документом (согласно судьям), и нулю в противном случае. Наконец, MAP для коллекции поисковых запросов размера \(Q\) задается,
\[ \text{MAP} = \frac{\sum_{q=1}^Q \text{AveP}(q)}{Q}. \]Теперь вернемся к LambdaMART. Этот алгоритм реализует посписочный подход и использует градиентный бустинг для обучения функции ранжирования \(h(\mathbf{x})\). Затем бинарная модель \(f(\mathbf{x}_i, \mathbf{x}_k)\), которая предсказывает, должен ли документ \(\mathbf{x}_i\) иметь более высокий ранг, чем документ \(\mathbf{x}_k\) (по тому же поисковому запросу), задается сигмоидом с гиперпараметром \(\alpha\),
\[ f(\mathbf{x}_i, \mathbf{x}_k) \stackrel{\text{def}}{=} \frac{1}{1 + \exp(h(\mathbf{x}_i) - h(\mathbf{x}_k))\alpha}. \]Опять же, как и во многих моделях, предсказывающих вероятность, функция стоимости — это перекрестная энтропия, вычисленная с использованием модели \(f\). В нашем градиентном бустинге мы комбинируем несколько регрессионных деревьев для построения функции \(h\), пытаясь минимизировать стоимость. Помните, что в градиентном бустинге мы добавляем дерево к модели, чтобы уменьшить ошибку, которую текущая модель допускает на обучающих данных. Для задачи классификации мы вычисляли производную функции стоимости, чтобы заменить реальные метки обучающих примеров этими производными. LambdaMART работает аналогично, с одним исключением. Он заменяет реальный градиент комбинацией градиента и другого фактора, который зависит от метрики, такой как MAP. Этот фактор изменяет исходный градиент, увеличивая или уменьшая его так, чтобы значение метрики улучшалось.
Это очень яркая идея, и не многие алгоритмы обучения с учителем могут похвастаться тем, что они оптимизируют метрику напрямую. Оптимизация метрики — это то, чего мы действительно хотим, но то, что мы делаем в типичном алгоритме обучения с учителем, — это оптимизируем стоимость вместо метрики (потому что метрики обычно не дифференцируемы). Обычно в обучении с учителем, как только мы нашли модель, которая оптимизирует функцию стоимости, мы пытаемся настроить гиперпараметры, чтобы улучшить значение метрики. LambdaMART оптимизирует метрику напрямую.
Оставшийся вопрос заключается в том, как мы строим ранжированный список результатов на основе предсказаний модели \(f\), которая предсказывает, должен ли ее первый вход быть ранжирован выше второго. В целом это вычислительно сложная проблема, и существует множество реализаций ранжировщиков, способных преобразовывать попарные сравнения в список ранжирования.
Самый простой подход — использовать существующий алгоритм сортировки. Алгоритмы сортировки сортируют коллекцию чисел в порядке возрастания или убывания. (Самый простой алгоритм сортировки называется пузырьковой сортировкой (bubble sort). Его обычно преподают в инженерных школах.) Обычно алгоритмы сортировки итеративно сравнивают пару чисел в коллекции и меняют их позиции в списке на основе результата этого сравнения. Если мы подключим нашу функцию \(f\) в алгоритм сортировки для выполнения этого сравнения, алгоритм сортировки будет сортировать документы, а не числа.
10.3 Обучение рекомендовать
Обучение рекомендовать (Learning to recommend) — это подход к построению рекомендательных систем (recommender systems). Обычно у нас есть пользователь, который потребляет контент. У нас есть история потребления, и мы хотим предложить этому пользователю новый контент, который ему понравится. Это может быть фильм на Netflix или книга на Amazon.
Традиционно для выдачи рекомендаций использовались два подхода: контентно-ориентированная фильтрация (content-based filtering) и коллаборативная фильтрация (collaborative filtering).
Контентно-ориентированная фильтрация заключается в изучении того, что нравится пользователям, на основе описания контента, который они потребляют. Например, если пользователь новостного сайта часто читает новостные статьи о науке и технологиях, то мы будем предлагать этому пользователю больше документов о науке и технологиях. В более общем случае мы могли бы создать один обучающий набор на пользователя и добавлять новостные статьи в этот набор данных в качестве вектора признаков \(\mathbf{x}\) и то, прочитал ли пользователь недавно эту новостную статью, в качестве метки \(y\). Затем мы строим модель каждого пользователя и можем регулярно проверять каждый новый фрагмент контента, чтобы определить, прочитает ли его конкретный пользователь.
Контентно-ориентированный подход имеет много ограничений. Например, пользователь может оказаться в ловушке так называемого фильтровального пузыря (filter bubble): система всегда будет предлагать этому пользователю информацию, очень похожую на ту, которую пользователь уже потреблял. Это может привести к полной изоляции пользователя от информации, которая не согласуется с его точкой зрения или расширяет ее. С более практической стороны, пользователи могут просто перестать следовать рекомендациям, что нежелательно. 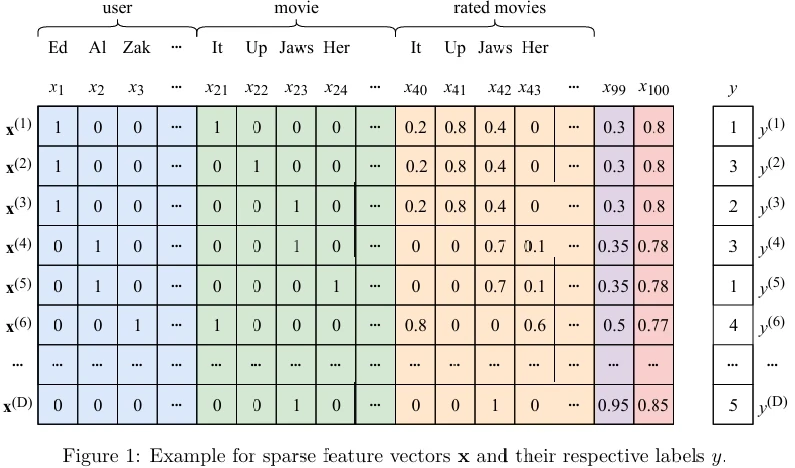
Коллаборативная фильтрация имеет значительное преимущество перед контентно-ориентированной фильтрацией: рекомендации для одного пользователя вычисляются на основе того, что потребляют или оценивают другие пользователи. Например, если два пользователя поставили высокие оценки одним и тем же десяти фильмам, то более вероятно, что пользователю 1 понравятся новые фильмы, рекомендованные на основе вкусов пользователя 2, и наоборот. Недостатком этого подхода является то, что содержание рекомендуемых элементов игнорируется.
В коллаборативной фильтрации информация о предпочтениях пользователей организована в матрицу. Каждая строка соответствует пользователю, а каждый столбец — элементу контента, который пользователь оценил или потребил. Обычно эта матрица огромна и чрезвычайно разрежена (sparse), что означает, что большинство ее ячеек не заполнены (или заполнены нулем). Причина такой разреженности в том, что большинство пользователей потребляют или оценивают лишь крошечную долю доступных элементов контента. Очень трудно давать осмысленные рекомендации на основе таких разреженных данных.
Большинство реальных рекомендательных систем используют гибридный подход (hybrid approach): они комбинируют рекомендации, полученные с помощью контентно-ориентированных и коллаборативных моделей фильтрации.
Я уже упоминал, что контентно-ориентированную рекомендательную модель можно построить с использованием модели классификации или регрессии, которая предсказывает, понравится ли пользователю контент на основе признаков контента. Примерами признаков могут быть слова в книгах или новостных статьях, которые понравились пользователю, цена, свежесть контента, личность автора контента и так далее.
Два эффективных алгоритма обучения рекомендательных систем — это факторизационные машины (factorization machines - FM) и шумоподавляющие автокодировщики (denoising autoencoders - DAE).
10.3.1 Факторизационные машины
Факторизационная машина — это относительно новый тип алгоритма. Он был явно разработан для разреженных наборов данных. Давайте проиллюстрируем проблему.
На Рисунке 1 (в pdf) вы видите пример разреженных векторов признаков с метками. Каждый вектор признаков представляет информацию об одном конкретном пользователе и одном конкретном фильме. Признаки в синем разделе представляют пользователя. Пользователи кодируются как one-hot векторы. Признаки в зеленом разделе представляют фильм. Фильмы также кодируются как one-hot векторы. Признаки в желтом разделе представляют нормализованные оценки, которые пользователь в синем поставил каждому фильму, который он оценил. Признак \(x_{99}\) представляет долю фильмов с Оскаром среди тех, которые пользователь посмотрел. Признак \(x_{100}\) представляет процент фильма, просмотренного пользователем в синем, прежде чем он оценил фильм в зеленом. Целевая переменная \(y\) — это оценка, данная пользователем в синем фильму в зеленом.
Реальные рекомендательные системы могут иметь миллионы пользователей, поэтому матрица на Рисунке 1 может насчитывать сотни миллионов строк. Количество признаков также может исчисляться миллионами, в зависимости от того, насколько богат выбор контента и насколько креативны вы, как аналитик данных, в инженерии признаков. Признаки \(x_{99}\) и \(x_{100}\) были созданы вручную в процессе инженерии признаков, и я показываю только два признака в целях иллюстрации.
Попытка подогнать модель регрессии или классификации к такому чрезвычайно разреженному набору данных привела бы к плохой обобщающей способности. Факторизационные машины подходят к этой проблеме по-другому.
Модель факторизационной машины определяется следующим образом:
\[ f(\mathbf{x}) \stackrel{\text{def}}{=} b + \sum_{i=1}^D w_i x_i + \sum_{i=1}^D \sum_{j=i+1}^D (\mathbf{v}_i \mathbf{v}_j) x_i x_j, \]где \(b\) и \(w_i\), \(i = 1, \dots, D\), — скалярные параметры, аналогичные тем, что используются в линейной регрессии. Векторы \(\mathbf{v}_i\) — это \(k\)-мерные векторы факторов (factors). \(k\) — гиперпараметр, и обычно он намного меньше \(D\). Выражение \(\mathbf{v}_i \mathbf{v}_j\) — это скалярное произведение \(i\)-го и \(j\)-го векторов факторов. Как вы можете видеть, вместо поиска одного широкого вектора параметров, который может плохо отражать взаимодействия между признаками из-за разреженности, мы дополняем его дополнительными параметрами, которые применяются к попарным взаимодействиям \(x_i x_j\) между признаками. Однако вместо того, чтобы иметь параметр \(w_{i,j}\) для каждого взаимодействия, что добавило бы огромное1 количество новых параметров к модели, мы факторизуем \(w_{i,j}\) в \(\mathbf{v}_i \mathbf{v}_j\), добавляя только \(Dk \ll D(D - 1)\) параметров к модели2.
В зависимости от проблемы, функцией потерь может быть потеря в виде квадрата ошибки (для регрессии) или шарнирная потеря. Для классификации с \(y \in \{-1, +1\}\), с шарнирной потерей или логистической потерей предсказание делается как \(y = \text{sign}(f(\mathbf{x}))\). Логистическая потеря определяется как,
\[ \text{loss}(f(\mathbf{x}), y) = \frac{1}{\ln 2} \ln(1 + e^{-yf(\mathbf{x})}). \]Градиентный спуск может использоваться для оптимизации средней потери. В примере на Рисунке 1 метки находятся в \(\{1, 2, 3, 4, 5\}\), так что это многоклассовая проблема. Мы можем использовать стратегию «один против остальных», чтобы преобразовать эту многоклассовую проблему в пять задач бинарной классификации.
10.3.2 Шумоподавляющие автокодировщики
Из Главы 7 вы знаете, что такое шумоподавляющий автокодировщик: это нейронная сеть, которая реконструирует свой вход из слоя узкого места. Тот факт, что вход искажен шумом, а выход — нет, делает шумоподавляющие автокодировщики идеальным инструментом для построения рекомендательной модели.
Идея очень проста: новые фильмы, которые могли бы понравиться пользователю, рассматриваются так, как если бы они были удалены из полного набора предпочитаемых фильмов некоторым процессом искажения. Цель шумоподавляющего автокодировщика — реконструировать эти удаленные элементы.
Чтобы подготовить обучающий набор для нашего шумоподавляющего автокодировщика, удалите синие и зеленые признаки из обучающего набора на Рисунке 1. Поскольку теперь некоторые примеры становятся дубликатами, сохраните только уникальные.
Во время обучения случайным образом заменяйте некоторые ненулевые желтые признаки во входных векторах признаков нулями. Обучите автокодировщик реконструировать неискаженный вход.
Во время предсказания постройте вектор признаков для пользователя. Вектор признаков будет включать неискаженные желтые признаки, а также созданные вручную признаки, такие как \(x_{99}\) и \(x_{100}\). Используйте обученную модель DAE для реконструкции неискаженного входа. Рекомендуйте пользователю фильмы, имеющие самые высокие оценки на выходе модели.
Другой эффективной моделью коллаборативной фильтрации является FFNN с двумя входами и одним выходом. Помните из Главы 8, что нейронные сети хорошо справляются с обработкой нескольких одновременных входов. Обучающий пример здесь — тройка \((u, m, r)\). Входной вектор \(\mathbf{u}\) — это one-hot кодирование пользователя. Второй входной вектор \(\mathbf{m}\) — это one-hot кодирование фильма. Выходной слой может быть либо сигмоидом (в этом случае метка \(r\) находится в \([0, 1]\)), либо ReLU, в этом случае \(r\) может быть в некотором типичном диапазоне, \([1, 5]\), например.
10.4 Самообучение: Вложения слов
Мы уже обсуждали вложения слов (word embeddings) в Главе 7. Напомним, что вложения слов — это векторы признаков, которые представляют слова. Они обладают свойством, что похожие слова имеют похожие векторы признаков. Вопрос, который вы, вероятно, хотели задать, — откуда берутся эти вложения слов. Ответ (опять же): они изучаются из данных.
Существует много алгоритмов для изучения вложений слов. Здесь мы рассмотрим только один из них: word2vec, и только одну версию word2vec, называемую skip-gram, которая хорошо работает на практике. Предварительно обученные вложения word2vec для многих языков доступны для загрузки онлайн.
При изучении вложений слов наша цель — построить модель, которую мы можем использовать для преобразования one-hot кодирования слова во вложение слова. Пусть наш словарь содержит 10 000 слов.
One-hot вектор для каждого слова — это 10 000-мерный вектор из всех нулей, за исключением одного измерения, которое содержит 1. Разные слова имеют 1 в разных измерениях.
Рассмотрим предложение: «Я почти закончил читать книгу по машинному обучению». Теперь рассмотрим то же предложение, из которого мы удалили одно слово, скажем, «книгу». Наше предложение становится: «Я почти закончил читать · по машинному обучению». Теперь оставим только три слова до · и три слова после: «закончил читать · по машинному обучению». Глядя на это семисловное окно вокруг ·, если я попрошу вас угадать, что означает ·, вы, вероятно, скажете: «книгу», «статью» или «работу». Вот как контекстные слова позволяют вам предсказать слово, которое они окружают. Это также то, как машина может узнать, что слова «книга», «работа» и «статья» имеют схожее значение: потому что они разделяют схожие контексты во многих текстах.
Оказывается, это работает и в обратную сторону: слово может предсказать контекст, который его окружает. Фрагмент «закончил читать · по машинному обучению» называется скип-граммой (skip-gram) с размером окна 7 (3 + 1 + 3). Используя документы, доступные в Интернете, мы можем легко создать сотни миллионов скип-грамм.
Обозначим скип-грамму так: \([\mathbf{x}_{-3}, \mathbf{x}_{-2}, \mathbf{x}_{-1}, \mathbf{x}, \mathbf{x}_{+1}, \mathbf{x}_{+2}, \mathbf{x}_{+3}]\). В нашем предложении \(\mathbf{x}_{-3}\) — это one-hot вектор для «закончил», \(\mathbf{x}_{-2}\) соответствует «читать», \(\mathbf{x}\) — пропущенное слово (·), \(\mathbf{x}_{+1}\) — «по» и так далее. Скип-грамма с размером окна 5 будет выглядеть так: \([\mathbf{x}_{-2}, \mathbf{x}_{-1}, \mathbf{x}, \mathbf{x}_{+1}, \mathbf{x}_{+2}]\).
Модель скип-граммы с размером окна 5 схематически изображена на Рисунке 2 (в pdf). Это полносвязная сеть, как многослойный перцептрон. Входное слово — это то, которое обозначено как · в скип-грамме. Нейронная сеть должна научиться предсказывать контекстные слова скип-граммы по центральному слову.
Теперь вы можете видеть, почему обучение такого рода называется самообучением (self-supervised): размеченные примеры извлекаются из неразмеченных данных, таких как текст.
Функция активации, используемая в выходном слое, — softmax. Функция стоимости — отрицательный логарифм правдоподобия. Вложение для слова получается как выход слоя вложения, когда на вход модели подается one-hot кодирование этого слова.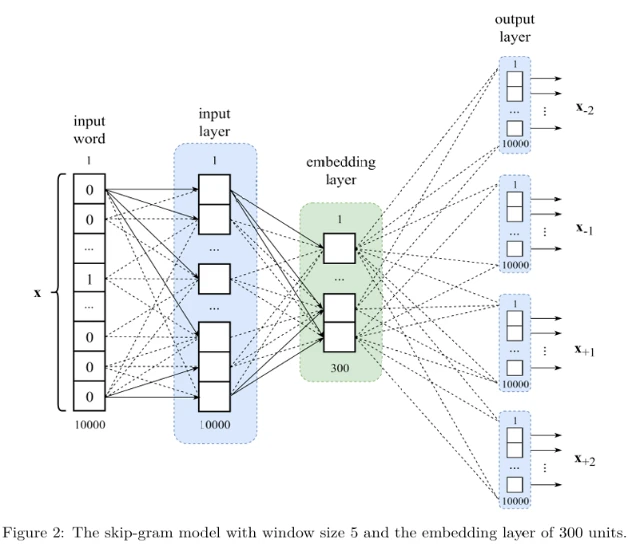
Из-за большого количества параметров в моделях word2vec используются две техники для повышения эффективности вычислений: иерархический softmax (hierarchical softmax) (эффективный способ вычисления softmax, который заключается в представлении выходов softmax как листьев бинарного дерева) и отрицательная выборка (negative sampling) (где идея заключается в обновлении только случайной выборки всех выходов за итерацию градиентного спуска). Я оставляю их для дальнейшего чтения.
1Точнее, мы бы добавили \(D(D - 1)\) параметров \(w_{i,j}\).
2Обозначение \(\ll\) означает «намного меньше чем».
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения