Глава 9. Обучение без учителя
Обучение без учителя (Unsupervised learning) имеет дело с проблемами, в которых данные не имеют меток. Это свойство делает его очень проблематичным для многих приложений. Отсутствие меток, представляющих желаемое поведение для вашей модели, означает отсутствие твердой точки отсчета для оценки качества вашей модели. В этой книге я представляю только методы обучения без учителя, которые позволяют строить модели, которые можно оценить на основе данных, а не человеческого суждения.
9.1 Оценка плотности
Оценка плотности (Density estimation) — это проблема моделирования функции плотности вероятности (pdf) неизвестного распределения вероятностей, из которого был взят набор данных. Она может быть полезна для многих приложений, в частности для обнаружения новизны (novelty detection) или обнаружения вторжений (intrusion detection). В Главе 7 мы уже оценивали pdf для решения задачи одноклассовой классификации. Для этого мы решили, что наша
модель будет параметрической (parametric), точнее, многомерным нормальным распределением (MND). Это решение было несколько произвольным, потому что если реальное распределение, из которого был взят наш набор данных, отличается от MND, наша модель, скорее всего, будет далека от идеальной. Мы также знаем, что модели могут быть непараметрическими (nonparametric). Мы использовали непараметрическую модель в ядерной регрессии. Оказывается, тот же подход может работать и для оценки плотности.
Пусть \({x_i}_{i=1}^N\) — одномерный набор данных (многомерный случай аналогичен), примеры которого были взяты из распределения с неизвестной pdf \(f\), где \(x_i \in \mathbb{R}\) для всех \(i = 1, \dots, N\). Нас интересует моделирование формы \(f\). Наша ядерная модель \(f\), обозначаемая как \(\hat{f}_b\), задается,
\[ \hat{f}_b(x) = \frac{1}{Nb} \sum_{i=1}^N k\left(\frac{x - x_i}{b}\right), \quad (1) \]где \(b\) — гиперпараметр, который контролирует компромисс между смещением и дисперсией нашей модели, а \(k\) — ядро. Опять же, как и в Главе 7, мы используем гауссово ядро:
\[ k(z) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right). \]Мы ищем такое значение \(b\), которое минимизирует разницу между реальной формой \(f\) и формой нашей модели \(\hat{f}_b\). Разумным выбором меры этой разницы является так называемая средняя интегральная квадратичная ошибка (mean integrated squared error - MISE):
\[ \text{MISE}(b) = E\left[ \int_{\mathbb{R}} (\hat{f}_b(x) - f(x))^2 dx \right]. \quad (2) \]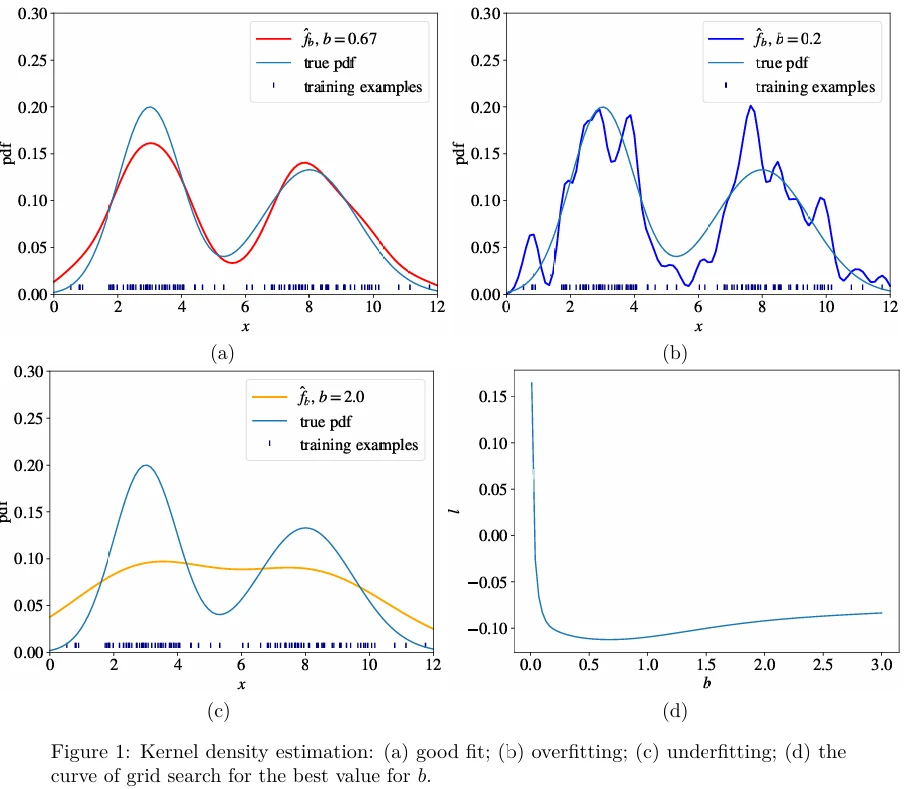
Интуитивно, вы видите в ур. 2, что мы возводим в квадрат разницу между реальной pdf \(f\) и нашей моделью \(\hat{f}_b\). Интеграл \(\int_{\mathbb{R}}\) заменяет суммирование \(\sum_{i=1}^N\), которое мы использовали в среднеквадратичной
ошибке, в то время как оператор математического ожидания E заменяет усреднение \(\frac{1}{N}\).
Действительно, когда наша потеря является функцией с непрерывной областью определения, такой как \((\hat{f}_b(x) - f(x))^2\), мы должны заменить суммирование интегралом. Операция математического ожидания E означает, что мы хотим, чтобы \(b\) было оптимальным для всех возможных реализаций нашего обучающего набора \({x_i}_{i=1}^N\). Это важно, потому что \(\hat{f}_b\) определена на конечной выборке некоторого распределения вероятностей, в то время как реальная pdf \(f\) определена на бесконечной области определения (множестве \(\mathbb{R}\)).
Теперь мы можем переписать правую часть в ур. 2 следующим образом:
\[ E\left[\int_{\mathbb{R}} \hat{f}_b^2(x)dx\right] - 2E\left[\int_{\mathbb{R}} \hat{f}_b(x)f(x)dx\right] + E\left[\int_{\mathbb{R}} f(x)^2dx\right]. \]Третий член в приведенной выше сумме не зависит от \(b\) и, следовательно, может быть проигнорирован. Несмещенной оценкой первого члена является \(\int_{\mathbb{R}} \hat{f}_b^2(x)dx\), в то время как несмещенная оценка второго члена может быть аппроксимирована с помощью перекрестной проверки (cross-validation) \(-\frac{2}{N}\sum_{i=1}^N \hat{f}_b^{(i)}(x_i)\), где \(\hat{f}_b^{(i)}\) — ядерная модель \(f\), вычисленная на нашем обучающем наборе с исключенным примером \(x_i\).
Член \(\sum_{i=1}^N \hat{f}_b^{(i)}(x_i)\) известен в статистике как оценка с исключением по одному (leave one out estimate), форма перекрестной проверки, в которой каждый блок состоит из одного примера. Вы могли заметить, что член \(\int_{\mathbb{R}} \hat{f}_b(x)f(x)dx\) (назовем его \(a\)) является математическим ожиданием функции \(\hat{f}_b\), потому что \(f\) является pdf. Можно продемонстрировать, что оценка с исключением по одному является несмещенной оценкой E[\(a\)].
Теперь, чтобы найти оптимальное значение \(b^*\) для \(b\), мы минимизируем стоимость, определяемую как,
\[ \int_{\mathbb{R}} \hat{f}_b^2(x)dx - \frac{2}{N} \sum_{i=1}^N \hat{f}_b^{(i)}(x_i). \]Мы можем найти \(b^*\) с помощью поиска по сетке. Для \(D\)-мерных векторов признаков \(\mathbf{x}\) член ошибки \(x - x_i\) в ур. 1 может быть заменен евклидовым расстоянием \(\|\mathbf{x} - \mathbf{x}_i\|\). На Рисунке 1 (в pdf) вы можете видеть оценки для одной и той же pdf, полученные с тремя различными значениями \(b\) из набора данных из 100 примеров, а также кривую поиска по сетке. Мы выбираем \(b^*\) в минимуме кривой поиска по сетке.
9.2 Кластеризация
Кластеризация (Clustering) — это проблема обучения присваивать метки примерам путем использования неразмеченного набора данных. Поскольку набор данных полностью не размечен, решение о том, является ли изученная модель оптимальной, гораздо сложнее, чем в обучении с учителем.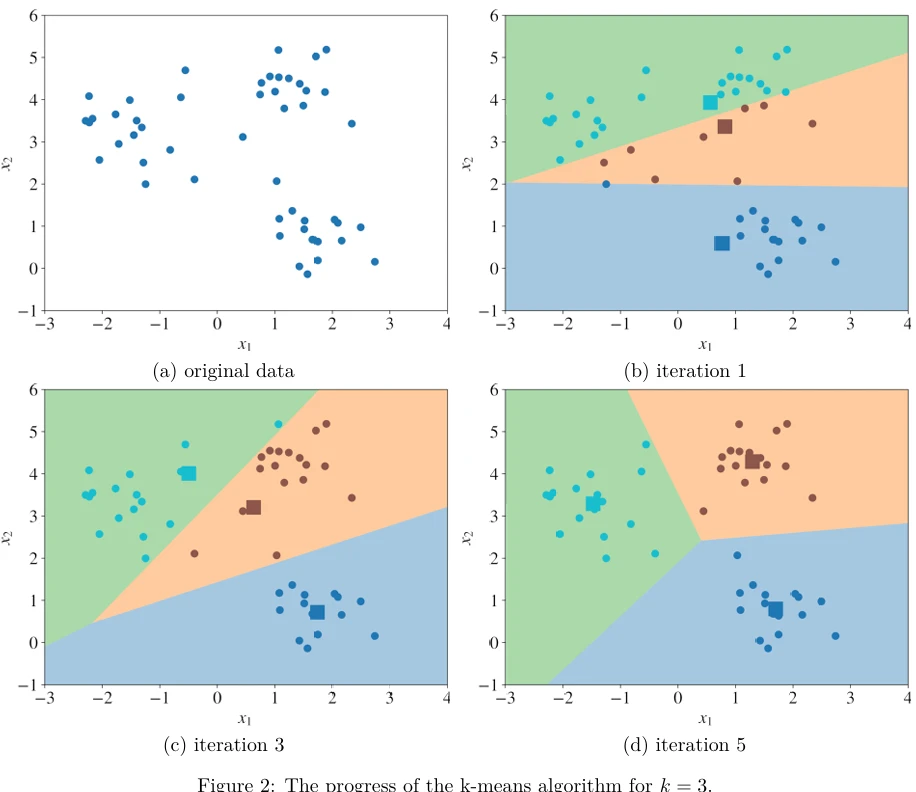
Существует множество алгоритмов кластеризации, и, к сожалению, трудно сказать, какой из них лучше по качеству для вашего набора данных. Обычно производительность каждого алгоритма зависит от неизвестных свойств распределения вероятностей, из которого был взят набор данных. В этой главе я описываю наиболее полезные и широко используемые алгоритмы кластеризации.
9.2.1 K-Средних
Алгоритм кластеризации k-средних (k-means) работает следующим образом. Сначала вы выбираете \(k\) — количество кластеров. Затем вы случайным образом помещаете \(k\) векторов признаков, называемых центроидами (centroids), в пространство признаков.
Затем мы вычисляем расстояние от каждого примера \(x\) до каждого центроида \(c\), используя некоторую метрику, например, евклидово расстояние. Затем мы присваиваем ближайший центроид каждому примеру (как если бы мы размечали каждый пример идентификатором центроида в качестве метки). Для каждого центроида мы вычисляем средний вектор признаков примеров, помеченных им. Эти средние векторы признаков становятся новыми местоположениями центроидов.
Мы пересчитываем расстояние от каждого примера до каждого центроида, изменяем присвоение и повторяем процедуру до тех пор, пока присвоения не перестанут меняться после пересчета местоположений центроидов. Модель — это список присвоений идентификаторов центроидов примерам.
Начальное положение центроидов влияет на окончательные положения, поэтому два запуска k-средних могут привести к двум разным моделям. Некоторые варианты k-средних вычисляют начальные положения центроидов на основе некоторых свойств набора данных.
Один запуск алгоритма k-средних иллюстрируется на Рисунке 2 (в pdf). Круги на Рисунке 2 — это двумерные векторы признаков; квадраты — это движущиеся центроиды. Разные цвета фона представляют регионы, в которых все точки принадлежат одному и тому же кластеру.
Значение \(k\), количество кластеров, является гиперпараметром, который должен быть настроен аналитиком данных. Существуют некоторые техники для выбора \(k\). Ни одна из них не доказана как оптимальная. Большинство этих техник требуют от аналитика сделать «обоснованное предположение», глядя на некоторые метрики или визуально изучая присвоения кластеров. В этой главе я представляю один подход к выбору разумно хорошего значения для \(k\) без взгляда на данные и угадывания.
9.2.2 DBSCAN и HDBSCAN
В то время как k-средних и подобные алгоритмы основаны на центроидах, DBSCAN является алгоритмом кластеризации на основе плотности (density-based). Вместо того чтобы угадывать, сколько кластеров вам нужно, с помощью DBSCAN вы определяете два гиперпараметра: \(\epsilon\) и \(n\). Вы начинаете с выбора примера \(x\) из вашего набора данных случайным образом и присваиваете его кластеру 1. Затем вы подсчитываете, сколько примеров имеют расстояние от \(x\) меньше или равное \(\epsilon\). Если это количество больше или равно \(n\), то вы помещаете всех этих \(\epsilon\)-соседей в тот же кластер 1. Затем вы изучаете каждого члена кластера 1 и находите их соответствующих \(\epsilon\)-соседей. Если какой-либо член кластера 1 имеет \(n\) или более \(\epsilon\)-соседей, вы расширяете кластер 1, добавляя этих \(\epsilon\)-соседей в кластер. Вы продолжаете расширять кластер 1 до тех пор, пока в него больше нельзя будет добавить примеров. В последнем случае вы выбираете из набора данных другой пример, не принадлежащий ни одному кластеру, и помещаете его в кластер 2. Вы продолжаете так до тех пор, пока все примеры либо не будут принадлежать какому-либо кластеру, либо не будут помечены как выбросы (outliers). Выброс — это пример, чье \(\epsilon\)-соседство содержит менее \(n\) примеров.
Преимущество DBSCAN заключается в том, что он может строить кластеры произвольной формы, в то время как k-средних и другие алгоритмы на основе центроидов создают кластеры, имеющие форму гиперсферы.
Очевидным недостатком DBSCAN является то, что он имеет два гиперпараметра, и выбор хороших значений для них (особенно для \(\epsilon\)) может быть сложным. Кроме того, при фиксированном \(\epsilon\) алгоритм кластеризации не может эффективно работать с кластерами разной плотности.
HDBSCAN — это алгоритм кластеризации, который сохраняет преимущества DBSCAN, устраняя необходимость решать значение \(\epsilon\). Алгоритм способен строить кластеры разной плотности. HDBSCAN — это гениальная комбинация нескольких идей, и полное описание алгоритма выходит за рамки этой книги.
HDBSCAN имеет только один важный гиперпараметр: \(n\), минимальное количество примеров для включения в кластер. Этот гиперпараметр относительно прост для выбора по интуиции. HDBSCAN имеет очень быстрые реализации: он может эффективно работать с миллионами примеров. Современные реализации k-средних намного быстрее, чем HDBSCAN, однако качества последнего могут перевесить его недостатки для многих практических задач. Я рекомендую всегда сначала пробовать HDBSCAN на ваших данных.
9.2.3 Определение количества кластеров
Самый важный вопрос — сколько кластеров содержит ваш набор данных? Когда векторы признаков одномерные, двумерные или трехмерные, вы можете посмотреть на данные и увидеть «облака» точек в пространстве признаков. Каждое облако — потенциальный кластер. Однако для \(D\)-мерных данных, с \(D > 3\), просмотр данных проблематичен1.
Один из способов определения разумного количества кластеров основан на концепции силы предсказания (prediction strength). Идея заключается в том, чтобы разделить данные на обучающий и тестовый наборы, аналогично тому, как мы делаем в обучении с учителем. Как только у вас есть обучающий и тестовый наборы, \(\mathcal{S}_{tr}\) размера \(N_{tr}\) и \(\mathcal{S}_{te}\) размера \(N_{te}\) соответственно, вы фиксируете \(k\), количество кластеров, и запускаете алгоритм кластеризации \(\mathcal{C}\) на наборах \(\mathcal{S}_{tr}\) и \(\mathcal{S}_{te}\) и получаете результаты кластеризации \(\mathcal{C}(\mathcal{S}_{tr}, k)\) и \(\mathcal{C}(\mathcal{S}_{te}, k)\).
Пусть \(A\) — кластеризация \(\mathcal{C}(\mathcal{S}_{tr}, k)\), построенная с использованием обучающего набора. Кластеры в \(A\) можно рассматривать как регионы. Если пример попадает в один из этих регионов, то этот пример принадлежит конкретному кластеру. Например, если мы применим алгоритм k-средних к некоторому набору данных, это приведет к разбиению пространства признаков на \(k\) многоугольных регионов, как мы видели на Рисунке 2.
Определим матрицу \(N_{te} \times N_{te}\) совместного членства (co-membership matrix) \(\mathbf{D}[A, \mathcal{S}_{te}]\) следующим образом: \(\mathbf{D}[A, \mathcal{S}_{te}]^{(i,i')} = 1\) тогда и только тогда, когда примеры \(x_i\) и \(x_{i'}\) из тестового набора принадлежат одному и тому же кластеру согласно кластеризации \(A\). В противном случае \(\mathbf{D}[A, \mathcal{S}_{te}]^{(i,i')} = 0\).
Давайте сделаем перерыв и посмотрим, что у нас есть. Мы построили, используя обучающий набор примеров, кластеризацию \(A\), которая имеет \(k\) кластеров. Затем мы построили матрицу совместного членства, которая указывает, принадлежат ли два примера из тестового набора одному и тому же кластеру в \(A\).
Интуитивно, если количество \(k\) является разумным числом кластеров, то два примера, принадлежащие одному и тому же кластеру в кластеризации \(\mathcal{C}(\mathcal{S}_{te}, k)\), скорее всего, будут принадлежать одному и тому же кластеру в кластеризации \(\mathcal{C}(\mathcal{S}_{tr}, k)\). С другой стороны, если \(k\) неразумно (слишком велико или слишком мало), то кластеризации на основе обучающих и тестовых данных, скорее всего, будут менее согласованными.
Используя данные, показанные на Рисунке 3 (в pdf), идея иллюстрируется на Рисунке 4 (в pdf). Графики на Рисунках 4a и 4b показывают соответственно \(\mathcal{C}(\mathcal{S}_{tr}, 4)\) и \(\mathcal{C}(\mathcal{S}_{te}, 4)\) с их соответствующими областями кластеров. Рисунок 4c показывает тестовые примеры, нанесенные на области кластеров обучающих данных. Вы можете видеть на 4c, что оранжевые тестовые примеры больше не принадлежат тому же кластеру согласно областям кластеризации, полученным из обучающих данных. Это приведет ко многим нулям в матрице \(\mathbf{D}[A, \mathcal{S}_{te}]\), что, в свою очередь, является индикатором того, что \(k = 4\), вероятно, не лучшее количество кластеров.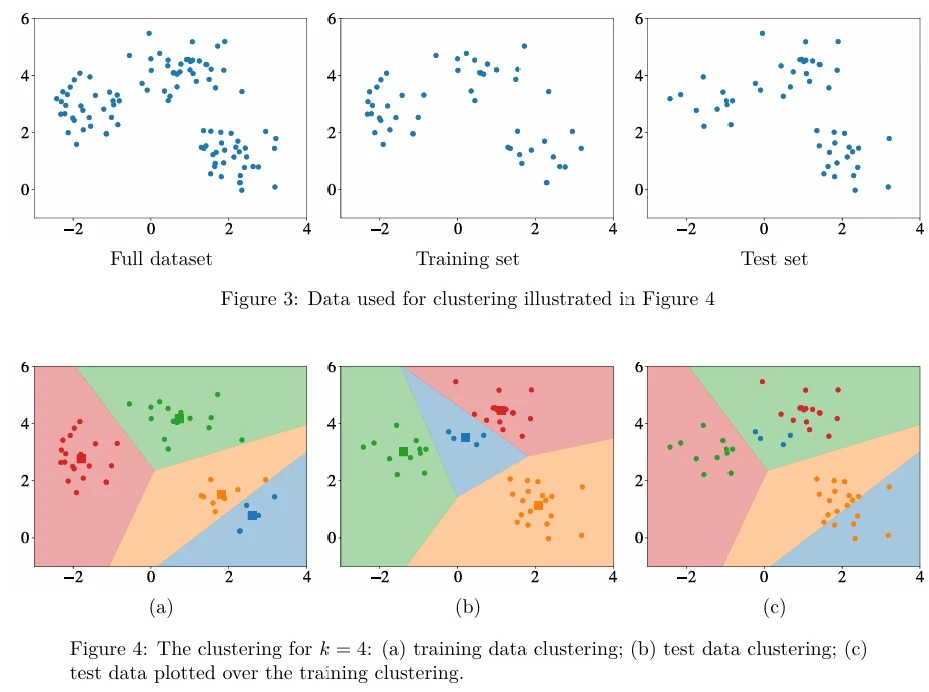
Более формально, сила предсказания для количества кластеров \(k\) задается,
\[ \text{ps}(k) \stackrel{\text{def}}{=} \min_{j=1,\dots,k} \frac{1}{|A_j|(|A_j| - 1)} \sum_{i,i' \in A_j} \mathbf{D}[A, \mathcal{S}_{te}]^{(i,i')}, \]где \(A \stackrel{\text{def}}{=} \mathcal{C}(\mathcal{S}_{tr}, k)\), \(A_j\) — \(j\)-й кластер из кластеризации \(\mathcal{C}(\mathcal{S}_{te}, k)\) и \(|A_j|\) — количество примеров в кластере \(A_j\).
Для данной кластеризации \(\mathcal{C}(\mathcal{S}_{tr}, k)\), для каждого тестового кластера мы вычисляем долю пар наблюдений в этом кластере, которые также отнесены к тому же кластеру центроидами обучающего набора. Сила предсказания — это минимум этой величины по \(k\) тестовым кластерам.
Эксперименты показывают, что разумное количество кластеров — это наибольшее \(k\), такое что \(\text{ps}(k)\) выше 0.8. Вы можете видеть на Рисунке 5 (в pdf) примеры предсказательной силы для разных значений \(k\) для данных с двумя, тремя и четырьмя кластерами.
Для недетерминированных алгоритмов кластеризации, таких как k-средних, которые могут генерировать разные кластеризации в зависимости от начальных положений центроидов, рекомендуется выполнять несколько запусков алгоритма кластеризации для одного и того же \(k\) и вычислять среднюю силу предсказания \(\bar{\text{ps}}(k)\) по нескольким запускам.
Другим эффективным методом оценки количества кластеров является метод статистики разрыва (gap statistic method). Другие, менее автоматические методы, которые некоторые аналитики все еще используют, включают метод локтя (elbow method) и метод среднего силуэта (average silhouette method).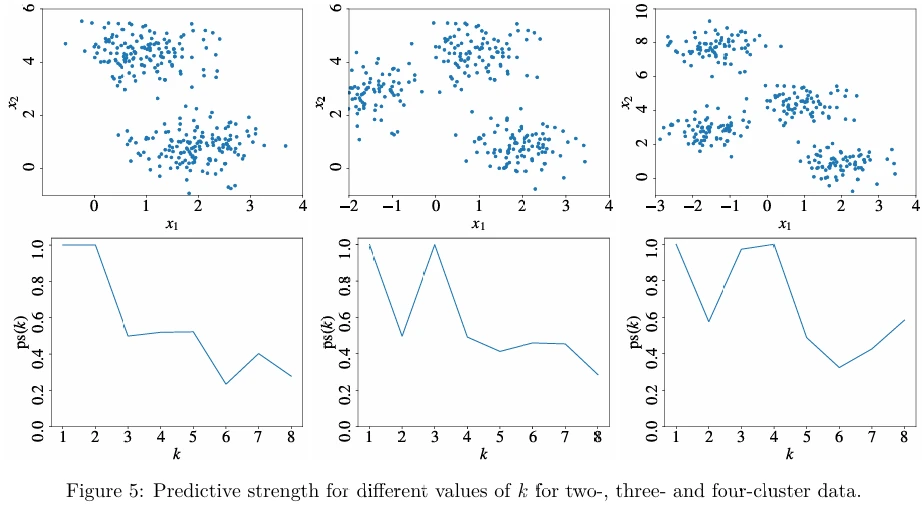
9.2.4 Другие алгоритмы кластеризации
DBSCAN и k-средних вычисляют так называемую жесткую кластеризацию (hard clustering), при которой каждый пример может принадлежать только одному кластеру. Модель гауссовой смеси (Gaussian mixture model - GMM) позволяет каждому примеру быть членом нескольких кластеров с разной оценкой принадлежности (membership score) (HDBSCAN также позволяет это). Вычисление GMM очень похоже на выполнение оценки плотности на основе модели. В GMM, вместо того чтобы иметь только одно многомерное нормальное распределение (MND), у нас есть взвешенная сумма нескольких MND:
\[ f_X = \sum_{j=1}^k \phi_j f_{\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j}, \]где \(f_{\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j}\) — это MND \(j\), а \(\phi_j\) — его вес в сумме. Значения параметров \(\boldsymbol{\mu}_j\), \(\boldsymbol{\Sigma}_j\) и \(\phi_j\) для всех \(j = 1, \dots, k\) получаются с использованием алгоритма максимизации ожидания (expectation maximization algorithm - EM) для оптимизации критерия максимального правдоподобия.
Опять же, для простоты, давайте рассмотрим одномерные данные. Также предположим, что есть два кластера: \(k = 2\). В этом случае у нас есть два гауссовских распределения,
\[ f(x | \mu_1, \sigma_1^2) = \frac{1}{\sqrt{2\pi\sigma_1^2}} \exp\left(-\frac{(x - \mu_1)^2}{2\sigma_1^2}\right) \quad \text{и} \quad f(x | \mu_2, \sigma_2^2) = \frac{1}{\sqrt{2\pi\sigma_2^2}} \exp\left(-\frac{(x - \mu_2)^2}{2\sigma_2^2}\right), \quad (3) \]где \(f(x | \mu_1, \sigma_1^2)\) и \(f(x | \mu_2, \sigma_2^2)\) — две pdf, определяющие правдоподобие \(X = x\).
Мы используем алгоритм EM для оценки \(\mu_1, \sigma_1^2, \mu_2, \sigma_2^2, \phi_1\) и \(\phi_2\). Параметры \(\phi_1\) и \(\phi_2\) полезны для оценки плотности и менее полезны для кластеризации, как мы увидим ниже.
EM работает следующим образом. В начале мы угадываем начальные значения для \(\mu_1, \sigma_1^2, \mu_2\) и \(\sigma_2^2\), и устанавливаем \(\phi_1 = \phi_2 = \frac{1}{2}\) (в общем случае это \(\frac{1}{k}\) для каждого \(\phi_j\), \(j \in 1, \dots, k\)).
На каждой итерации EM выполняются следующие четыре шага:
- Для всех \(i = 1, \dots, N\), вычислить правдоподобие каждого \(x_i\), используя ур. 3:
- Используя правило Байеса, для каждого примера \(x_i\), вычислить правдоподобие \(b_i^{(j)}\), что пример принадлежит кластеру \(j \in \{1, 2\}\) (другими словами, правдоподобие того, что пример был взят из гауссианы \(j\)):
Параметр \(\phi_j\) отражает, насколько вероятно, что наше гауссовское распределение \(j\) с параметрами \(\mu_j\) и \(\sigma_j^2\) могло породить наш набор данных. Вот почему в начале мы устанавливаем \(\phi_1 = \phi_2 = \frac{1}{2}\): мы не знаем, насколько вероятно каждое из двух гауссиан, и мы отражаем наше незнание, устанавливая правдоподобие обоих равным одной второй.
- Вычислить новые значения \(\mu_j\) и \(\sigma_j^2\), \(j \in \{1, 2\}\) как,
- Обновить \(\phi_j\), \(j \in \{1, 2\}\) как,
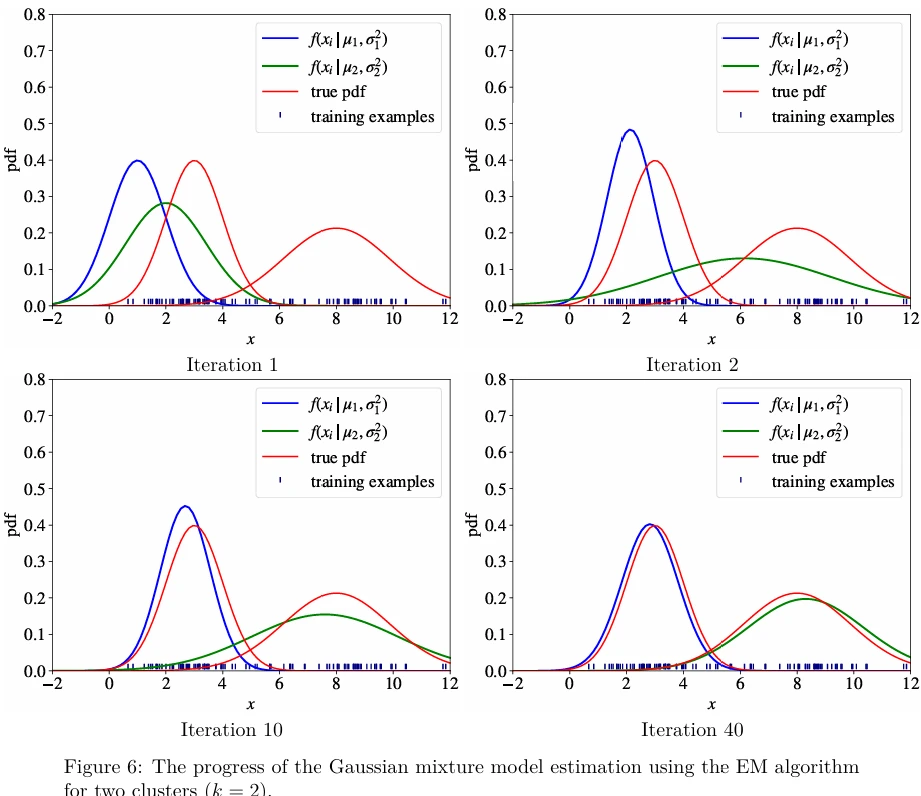
Шаги 1–4 выполняются итеративно до тех пор, пока значения \(\mu_j\) и \(\sigma_j^2\) не перестанут сильно меняться: например, изменение меньше некоторого порога \(\epsilon\). Рисунок 6 (в pdf) иллюстрирует этот процесс.
Вы могли заметить, что алгоритм EM очень похож на алгоритм k-средних: начать со случайных кластеров, затем итеративно обновлять параметры каждого кластера путем усреднения данных, которые отнесены к этому кластеру. Единственное отличие в случае GMM заключается в том, что присвоение примера \(x_i\) кластеру \(j\) является мягким (soft): \(x_i\) принадлежит кластеру \(j\) с вероятностью \(b_i^{(j)}\). Вот почему мы вычисляем новые значения для \(\mu_j\) и \(\sigma_j^2\) в ур. 4 не как среднее (используемое в k-средних), а как взвешенное среднее (weighted average) с весами \(b_i^{(j)}\).
Как только мы изучили параметры \(\mu_j\) и \(\sigma_j^2\) для каждого кластера \(j\), оценка принадлежности примера \(x\) кластеру \(j\) задается \(f(x | \mu_j, \sigma_j^2)\).
Расширение на \(D\)-мерные данные (\(D > 1\)) просто. Единственное отличие в том, что вместо дисперсии \(\sigma^2\) у нас теперь есть ковариационная матрица (covariance matrix) \(\boldsymbol{\Sigma}\), которая параметризует многомерное нормальное распределение (MND).
В отличие от k-средних, где кластеры могут быть только круглыми, кластеры в GMM имеют форму эллипса, который может иметь произвольное удлинение и вращение. Значения в ковариационной матрице контролируют эти свойства.
Нет общепризнанного метода выбора правильного \(k\) в GMM. Я рекомендую сначала разделить набор данных на обучающий и тестовый наборы. Затем вы пробуете разные \(k\) и строите разные модели \(f_{tr}^k\) для каждого \(k\) на обучающих данных. Вы выбираете значение \(k\), которое максимизирует правдоподобие примеров в тестовом наборе:
\[ \arg \max_k \prod_{i=1}^{|N_{te}|} f_{tr}^k(x_i), \]где \(|N_{te}|\) — размер тестового набора.
В литературе описано множество алгоритмов кластеризации. Стоит упомянуть спектральную кластеризацию (spectral clustering) и иерархическую кластеризацию (hierarchical clustering). Для некоторых наборов данных вы можете найти их более подходящими. Однако в большинстве практических случаев k-средних, HDBSCAN и модель гауссовой смеси удовлетворят ваши потребности.
9.3 Снижение размерности
Современные алгоритмы машинного обучения, такие как ансамблевые алгоритмы и нейронные сети, хорошо справляются с очень многомерными примерами, до миллионов признаков. С современными компьютерами и графическими процессорами (GPU) техники снижения размерности (dimensionality reduction) используются на практике реже, чем в прошлом. Наиболее частым случаем использования снижения размерности является визуализация данных (data visualization): люди могут интерпретировать максимум три измерения на графике.
Другая ситуация, в которой вы могли бы выиграть от снижения размерности, — это когда вам нужно построить интерпретируемую модель (interpretable model), и для этого вы ограничены в выборе алгоритмов обучения. Например, вы можете использовать только обучение деревьев решений или линейную регрессию. Уменьшая ваши данные до более низкой размерности и выясняя, какое качество исходного примера отражает каждый новый признак в пространстве признаков с пониженной размерностью, вы можете использовать более простые алгоритмы. Снижение размерности удаляет избыточные или сильно коррелированные признаки; оно также уменьшает шум в данных — все это способствует интерпретируемости модели.
Три широко используемые техники снижения размерности — это анализ главных компонент (principal component analysis - PCA), равномерное приближение и проекция многообразия (uniform manifold approximation and projection - UMAP) и автокодировщики (autoencoders).
Я уже объяснял автокодировщики в Главе 7. Вы можете использовать низкоразмерный выход слоя узкого места автокодировщика в качестве вектора пониженной размерности, который представляет высокоразмерный входной вектор признаков. Вы знаете, что этот низкоразмерный вектор представляет существенную информацию, содержащуюся во входном векторе, потому что автокодировщик способен реконструировать входной вектор признаков на основе выхода слоя узкого места.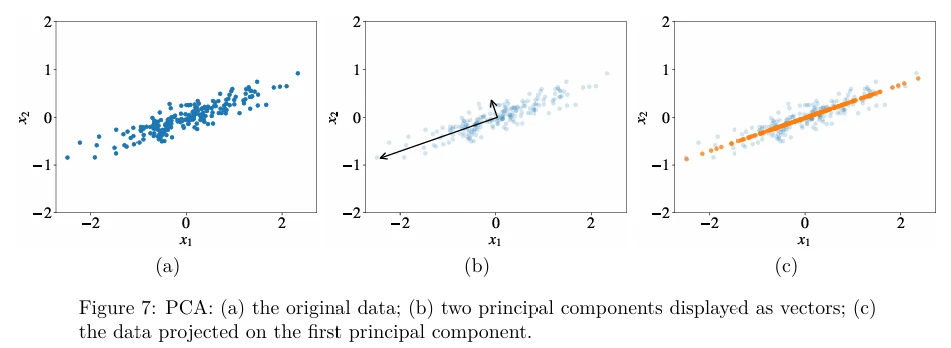
9.3.1 Анализ главных компонент
Анализ главных компонент или PCA — один из старейших методов снижения размерности. Математика, лежащая в его основе, включает операции над матрицами, которые я не объяснял в Главе
2, поэтому я оставляю математику PCA для вашего дальнейшего чтения. Здесь я предоставляю только интуицию и иллюстрирую метод на примере.
Рассмотрим двумерный набор данных, показанный на Рисунке 7a (в pdf). Главные компоненты (Principal components) — это векторы, которые определяют новую систему координат, в которой первая ось идет в направлении наибольшей дисперсии в данных. Вторая ось ортогональна первой и идет в направлении второй по величине дисперсии в данных. Если бы наши данные были трехмерными, третья ось была бы ортогональна как первой, так и второй осям и шла бы в направлении третьей по величине дисперсии, и так далее. На Рисунке 7b две главные компоненты показаны в виде стрелок. Длина стрелки отражает дисперсию в этом направлении.
Теперь, если мы хотим уменьшить размерность наших данных до \(D_{new} < D\), мы выбираем \(D_{new}\) наибольших главных компонент и проецируем наши точки данных на них. Для нашей двумерной иллюстрации мы можем установить \(D_{new} = 1\) и спроецировать наши примеры на первую главную компоненту, чтобы получить оранжевые точки на Рисунке 7c (в pdf).
Для описания каждой оранжевой точки нам нужна только одна координата вместо двух: координата относительно первой главной компоненты. Когда наши данные имеют очень высокую размерность, часто случается на практике, что первые две или три главные компоненты объясняют большую часть вариации в данных, поэтому, отображая данные на 2D или 3D графике, мы действительно можем увидеть очень многомерные данные и их свойства.
9.3.2 UMAP
Идея многих современных алгоритмов снижения размерности, особенно тех, которые разработаны специально для целей визуализации, таких как t-SNE и UMAP, в основном одинакова. Сначала мы разрабатываем метрику сходства для двух примеров. Для целей визуализации, помимо евклидова расстояния между двумя примерами, эта метрика сходства часто отражает некоторые локальные свойства двух примеров, такие как плотность других примеров вокруг них.
В UMAP эта метрика сходства \(w\) определяется следующим образом,
\[ w(x_i, x_j) \stackrel{\text{def}}{=} w_i(x_i, x_j) + w_j(x_j, x_i) - w_i(x_i, x_j)w_j(x_j, x_i). \quad (5) \]Функция \(w_i(x_i, x_j)\) определяется как,
\[ w_i(x_i, x_j) \stackrel{\text{def}}{=} \exp\left(-\frac{d(x_i, x_j) - \rho_i}{\sigma_i}\right), \]где \(d(x_i, x_j)\) — евклидово расстояние между двумя примерами, \(\rho_i\) — расстояние от \(x_i\) до его ближайшего соседа, а \(\sigma_i\) — расстояние от \(x_i\) до его \(k\)-го ближайшего соседа (\(k\) — гиперпараметр алгоритма).
Можно показать, что метрика в ур. 5 изменяется в диапазоне от 0 до 1 и является симметричной, что означает \(w(x_i, x_j) = w(x_j, x_i)\).
Пусть \(w\) обозначает сходство двух примеров в исходном высокоразмерном пространстве, а \(w'\) — сходство, заданное тем же ур. 5, в новом низкоразмерном пространстве.
Чтобы продолжить, мне нужно быстро ввести понятие нечеткого множества (fuzzy set). Нечеткое множество — это обобщение множества. Для каждого элемента \(x\) в нечетком множестве \(\mathcal{S}\) существует функция принадлежности (membership function) \(\mu_{\mathcal{S}}(x) \in [0, 1]\), которая определяет степень принадлежности (membership strength) \(x\) множеству \(\mathcal{S}\). Мы говорим, что \(x\) слабо принадлежит нечеткому множеству \(\mathcal{S}\), если \(\mu_{\mathcal{S}}(x)\) близко к нулю. С другой стороны, если \(\mu_{\mathcal{S}}(x)\) близко к 1, то \(x\) имеет сильную принадлежность к \(\mathcal{S}\). Если \(\mu(x) = 1\) для всех \(x \in \mathcal{S}\), то нечеткое множество \(\mathcal{S}\) становится эквивалентным нормальному, не нечеткому множеству.
Давайте теперь посмотрим, зачем нам здесь нужно это понятие нечеткого множества.
Поскольку значения \(w\) и \(w'\) лежат в диапазоне от 0 до 1, мы можем рассматривать \(w(x_i, x_j)\) как принадлежность пары примеров \((x_i, x_j)\) к определенному нечеткому множеству. То же самое можно сказать и о \(w'\). Понятие сходства двух нечетких множеств называется перекрестной энтропией нечетких множеств (fuzzy set cross-entropy) и определяется как,
\[ C_{w,w'} = \sum_{i=1}^N \sum_{j=1}^N \left[ w(x_i, x_j) \ln\left(\frac{w(x_i, x_j)}{w'(x'_i, x'_j)}\right) + (1 - w(x_i, x_j)) \ln\left(\frac{1 - w(x_i, x_j)}{1 - w'(x'_i, x'_j)}\right) \right], \quad (6) \]где \(x'\) — низкоразмерная «версия» исходного высокоразмерного примера \(x\).
В ур. 6 неизвестными параметрами являются \(x'_i\) (для всех \(i = 1, \dots, N\)), низкоразмерные примеры, которые мы ищем. Мы можем вычислить их с помощью градиентного спуска, минимизируя \(C_{w,w'}\).
На Рисунке 8 (в pdf) вы можете видеть результат снижения размерности, примененного к набору данных MNIST рукописных цифр. MNIST обычно используется для сравнительного анализа различных систем обработки изображений;
он содержит 70 000 размеченных примеров. Десять разных цветов на графике соответствуют десяти классам. Каждая точка на графике соответствует конкретному примеру в наборе данных. Как вы можете видеть, UMAP разделяет примеры визуально лучше (помните, у него нет доступа к меткам). На практике UMAP немного медленнее, чем PCA, но быстрее, чем автокодировщик.
9.4 Обнаружение выбросов
Обнаружение выбросов (Outlier detection) — это проблема обнаружения примеров в наборе данных, которые сильно отличаются от того, как выглядит типичный пример в наборе данных. Мы уже видели несколько техник, которые могут помочь решить эту проблему: автокодировщик и обучение одноклассового классификатора. Если мы используем автокодировщик, мы обучаем его на нашем наборе данных. Затем, если мы хотим предсказать, является ли пример выбросом, мы можем использовать модель автокодировщика для реконструкции примера из слоя узкого места. Модель вряд ли сможет реконструировать выброс.
При одноклассовой классификации модель либо предсказывает, что входной пример принадлежит классу, либо что это выброс.
1Некоторые аналитики смотрят на несколько двумерных графиков, на которых присутствует только пара признаков одновременно. Это может дать интуицию о количестве кластеров. Однако такой подход страдает от субъективности, подвержен ошибкам и считается скорее обоснованным предположением, чем научным методом.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения