Ai for data science

Глава 7: Создание оптимизатора на основе генетических алгоритмов

Генетический алгоритм (GA) — популярный метод оптимизации, предшествующий большинству аналогичных подходов, вдохновленных природой. Он является частью семейства методов эволюционных вычислений, которые представляют собой очень надежный вид ИИ. Хотя этот подход к оптимизации был впервые представлен в 1960-х годах Инго Рехенбергом, фреймворк GA не был полностью реализован до чуть более позднего времени, в начале 1970-х годов, командой Джона Холланда. Джон Холланд популяризировал этот новый подход в своей книге «Адаптация в природных и искусственных системах», опубликованной в 1975 году.

ГА сильно зависят от дарвиновской эволюции. Идея заключается в том, что каждое решение является частью группы клеток, которые развиваются на протяжении ряда поколений (эквивалент эпох в ANN и итераций в PSO). По мере эволюции группы она приближается к оптимальному решению задачи оптимизации, которую она моделирует.

Мы рассмотрим специфику фреймворка генетических алгоритмов и его основной алгоритм, посмотрим, как реализовать его на Julia, укажем несколько вариантов и обсудим применимость генетических алгоритмов в науке о данных.

Идея фреймворка ГА состоит в том, чтобы рассматривать проблему как набор дискретных элементов, формирующих то, что называется хромосомой. Каждый из этих элементов называется геном, и их количество может быть произвольным, в зависимости от решаемой задачи. Хотя каждый ген обычно представляет собой бит, кодирование может принимать различные формы.14 Набор всех этих хромосом называется геномом. Через ряд процессов геном эволюционирует в идеальную комбинацию генов. Эта «идеальная комбинация» называется «генотипом», и она заключает в себе решение, которое мы ищем. Информация, заключенная в кодировании каждого гена, называется признаком.

В отличие от PSO, элементы решения ГА меняются не за счет движения, а за счет пары процессов, называемых мутацией и кроссинговером. Эти термины снова заимствованы из биологии, так как процессы аналогичны тем, которые происходят при репликации ДНК. В природе этот процесс приводит к рождению новых организмов; именно поэтому мы называем различные итерации этого эволюционного процесса «поколениями».

Мутация — самый простой процесс, так как он затрагивает одну хромосому. По сути, он гарантирует, что на протяжении каждого поколения существует шанс, что какой-либо ген в хромосоме случайно изменится. Вероятность этого невелика, но весь эволюционный процесс занимает столько времени, что это практически гарантированно произойдет хотя бы один раз. Более того, теоретически возможно наличие множественных мутаций в одной и той же хромосоме (особенно если она достаточно большая). Цель мутации в том, чтобы обеспечить разнообразие признаков, которые в противном случае остались бы неизменными.

Кроссинговер (или рекомбинация) — наиболее распространенный процесс изменения элементов. Он включает слияние двух хромосом в одну, либо в случайном, либо в заранее определенном месте, например, посередине, как видно на
Рисунке 6

Рисунок 6: Процесс кроссинговера для пары простых хромосом. Обратите внимание, что место кроссинговера может быть любым на хромосоме, а также в нескольких точках.

Однако, некоторые случаи кроссинговера могут затрагивать два места, или даже логический оператор, такой как И. Для простоты, в этой главе мы будем работать с базовым одноточечным кроссинговером.

Процесс кроссинговера гарантирует, что геном со временем меняется за счет признаков, которые уже проявляются у родителей (например, цвет глаз). Какие из этих

признаков выживают в долгосрочной перспективе, зависит от другого аспекта эволюционного процесса, называемого приспособленностью. Не все хромосомы проходят кроссинговер, поскольку существует процесс отбора, гарантирующий, что наиболее приспособленные хромосомы с наибольшей вероятностью будут иметь потомство в следующем поколении, во многом как в виде, только более приспособленные особи (например, быстрее, более адаптируемые, с лучшей иммунной системой и т. д.) выживают и размножаются, гарантируя, что их гены не вымрут.

Приспособленность — это мера того, насколько хорошо эти хромосомы работают как потенциальные решения проблемы, которую мы решаем. Как и в случае с PSO, мы пытаемся максимизировать или минимизировать функцию приспособленности, которая оценивает решение. Поскольку количество хромосом должно оставаться постоянным на протяжении всего эволюционного процесса (иначе мы рискуем получить взрыв популяции, истощающий наши вычислительные ресурсы), в следующее поколение попадают только лучшие хромосомы, исходя из их приспособленности.

Элитизм — вспомогательный аспект фреймворка ГА, который часто используется для обеспечения постоянного присутствия наилучшего решения. Это как предохранитель, защищающий от возможности того, что новый геном будет хуже предыдущего поколения из-за плохих кроссинговеров и/или плохих мутаций. Элитизм гарантирует, что наилучшая хромосома или хромосомы остаются в следующем поколении независимо от этого.

Хотя элитизм не был частью оригинального фреймворка ГА, настоятельно рекомендуется его использовать, так как доказано, что он, как правило, улучшает производительность оптимизатора. Однако, если вы переусердствуете с элитизмом, передавая слишком много хорошо работающих хромосом в следующее поколение за счет других, не столь хорошо работающих хромосом, вы можете получить слишком однородную популяцию. Это приведет к процессу оптимизации, который преждевременно сходится с вероятностью того, что полученное решение будет субоптимальным. Обратите внимание, что опция элитизма контролируется параметром, указывающим, сколько наилучших хромосом сохранять (см. функцию elitism() далее).

Пространство поиска задач, решаемых с помощью ГА, идеально включает огромное количество потенциальных решений задачи — обычно больше, чем можно было бы решить аналитически. Скромный пример: если ГА попытается решить задачу, где каждая хромосома имеет 60 генов, представленных в виде битов, то она будет иметь 2⁶⁰ или более миллиарда миллиардов потенциальных решений.

В общем, задачи, которые хорошо решаются с помощью ГА, подпадают под зонтик

«NP-трудных» задач. Это задачи, решение которых нельзя свести к быстрому процессу, так как они занимают экспоненциальное время. Это означает, что если размерность задачи увеличится в 2 раза, сложность задачи обязательно увеличится в 4 раза или более.

Типичная NP-трудная задача с множеством приложений в логистике — задача коммивояжера (TSP). Она включает поиск оптимального способа пройти по графу так, чтобы в конце путешествия вернуться туда, откуда вы начали. Несмотря на простое описание, это исключительно сложная задача по мере увеличения числа узлов в графе.

Поскольку масштабы этих задач делают поиск наилучшего решения совершенно нереалистичным, мы выбираем «достаточно хорошее» решение — то, которое дает довольно большое (или малое) значение функции приспособленности, которую мы пытаемся максимизировать или минимизировать.

Стандартный генетический алгоритм

Теперь давайте рассмотрим реальный алгоритм, лежащий в основе фреймворка ГА, — сам оригинальный генетический алгоритм. Основной процесс выглядит следующим образом:

1. Этап инициализации: Создание случайной популяции из n хромосом (потенциальных решений задачи). Определение функции приспособленности F() и режима оптимизации (максимизация или минимизация). Определение условий остановки, таких как максимальное число поколений или минимальный прогресс приспособленности за заданное число поколений. Определение вероятностей кроссовера и мутации (соответственно p_c и p_m), а также схемы отбора.
2. Оценка приспособленности: Оценка приспособленности каждой хромосомы x в популяции путем вычисления F(x).
3. Новая популяция: Создание нового генома путем повторения следующих шагов до тех пор, пока новый набор хромосом не будет завершен:
1. Отбор: Выбор двух родительских хромосом из популяции в соответствии с их приспособленностью. А именно, выбор

их с вероятностью p, пропорциональной их показателям приспособленности.

2. Кроссинговер: С вероятностью кроссинговера p_c, кроссинговер родителей для образования нового потомства (детей). Если кроссинговер не выполняется, потомство является точными копиями их родителей.
3. Мутация: С вероятностью мутации p_m, мутация нового потомства в каждой позиции.
4. Обновление популяции: Помещение нового потомства в новую популяцию и отбрасывание предыдущей популяции.

4. Процесс цикла: Повторение шагов 2-3 до тех пор, пока не будет выполнено условие остановки.
5. Результаты вывода: Вывод наиболее эффективно работающей хромосомы и ее показателя приспособленности.

Процесс отбора включает один из двух основных методов стохастического определения того, какие хромосомы становятся родителями (кандидатами на участие в процессе кроссинговера), а какие нет. Это отбор рулеткой и ранговый отбор.

Первый подход включает создание «рулетки», основанной на показателях приспособленности всех хромосом, путем их нормализации таким образом, чтобы их сумма была равна 1. Эта нормализация происходит на основе функции масштабирования, такой как exp(x) или sqrt(x), в зависимости от решаемой задачи. После этого мы получаем случайное число в интервале [0, 1) и выбираем хромосому, соответствующую сегменту рулетки, который включает это случайное число. Затем мы повторяем этот процесс еще раз, чтобы найти другого родителя.

Подход рангового отбора использует ранжирование значений приспособленности вместо самих значений. Таким образом, наименее приспособленная хромосома будет иметь значение 1, вторая по приспособленности — 2, а лучшая — значение n, где n — общее количество хромосом. Во всех остальных аспектах он такой же, как и подход рулетки. Подход рангового отбора гарантирует, что все хромосомы имеют приличный шанс быть выбранными,

особенно в случаях, когда небольшое количество хромосом доминирует в популяции с точки зрения производительности (потому что они значительно лучше остальных).

При таком большом количестве параметров в фреймворке ГА может быть сложно понять, как его использовать для решения задач оптимизации. Ниже приведены некоторые эмпирические правила для выбора значений этих параметров. Естественно, экспериментирование с этими параметрами — отличный способ научиться, но эти рекомендации помогут вам хотя бы начать.

Что касается кроссовера, вы можете использовать вероятность от 0.8 до 0.95. Это означает, что примерно в 90% случаев для данной хромосомы будет происходить кроссовер.

Что касается вероятности мутации, то значение около 0.005-0.01 обычно работает. Со временем мутация сама по себе может дать неплохое решение без кроссинговера вообще. Слишком высокое значение приведет к очень нестабильному геному, который будет неконтролируемо изменяться и никогда не сойдется.

Размер популяции установить немного сложнее, поскольку большая популяция все равно будет работать, но выполнение алгоритма займет больше времени. Именно поэтому иметь количество хромосом, равное количеству генов в хромосоме, — хорошее место для начала.

Что касается типа отбора, то обычно метод рулетки подходит. Однако, если вы обнаружите, что небольшой набор хромосом монополизирует процесс решения (что приводит к в значительной степени субоптимальным результатам для всей системы), то ранговый отбор может быть лучшим вариантом.

Реализация ГА в Julia

Теперь давайте посмотрим, как этот алгоритм может быть реализован на Julia. Ниже приведен пример реализации ГА с включенным дополнением элитизма. Мы также включили пример функции приспособленности, чтобы вы могли ее протестировать. Обратите внимание, что некоторые переменные в этом коде сокращены. Они означают следующее:

• X = данные популяции (матрица)
• c = вектор коэффициентов для функции-образца, для целей тестирования
• ff = функция приспособленности для максимизации

• nv = количество переменных для рассмотрения
• maximize = нужно ли максимизировать функцию
• ips = начальный размер популяции
• s = желаемая сумма хромосом в генерируемой популяции (необязательный, но полезный параметр для определенных задач)
• px = вероятность события x
• ng = количество поколений

Код написан таким образом, чтобы его можно было легко настраивать по мере необходимости, в соответствии с парадигмой функционального программирования Julia, которая выглядит следующим образом:

function sample_ff(x::Array{<:Real, 1},
c::Array{<:Real, 1} = ones(Int64, length(x))) #
function to maximize
z = abs.(x) .* c
return 1 / (1 + sum(z))
end
ShouldActivate(p::Float64) = rand() < p #
activation trigger for an event of probability p
evaluation(ff::Function, x::Array{<:Real, 1}) =
ff(x)
function scaling(y::Array{Float64, 1}) # scaling
fitness function values
y_ = exp(y)
# y_ = sqrt(y) # another alternative for scaling
return y_ / sum(y_)
end
function selection(X::Array{<:Real, 2},
y::Array{Float64, 1}, nv::Int64, ips::Int64)
y_ = scaling(y)
c = 0
ind = 1
xs = Array{eltype(X)}(undef, 2, nv)
ys = Array{Float64}(undef, 2)
while true

if ShouldActivate(y_[ind])
c += 1
xs[c, :] = X[ind, :]
ys[c] = y[ind]
if c == 2; return xs, ys; end
end
ind += 1
if ind > ips; ind = 1; end
end
end
function mutation(x::Array{<:Real, 1},
p::Float64, nv::Int64) # change population a bit
new = false
for i = 1:nv
if ShouldActivate(p)
new = true
if eltype(x) <: Bool
x[i] = !x[i]
else
x[i] = 1 - x[i]
end
end
end
return x, new
end
function crossover(xs::Array{<:Real, 2},
ys::Array{Float64, 1}, p::Float64, nv::Int64)
d = rand(1:2) # dominant gene
z = xs[d, :]
w = ys[d]
new = false
if ShouldActivate(p)
new = true
r = 3 - d # recessive gene
q = rand(1:(nv-1))
z[1:q] = xs[r, 1:q]
w = [NaN]

end
return z, w, new
end
function elitism(X::Array{<:Integer, 2},
y::Array{Float64, 1}, n::Int64)
YX = hcat(y, X)
YX_sorted = swi(YX)[1]
X_elite = round.(Int64, YX_sorted[1:n,
2:end])
y_elite = YX_sorted[1:n, 1]
return X_elite, y_elite
end
function GeneratePopulation(ips::Int64,
nv::Int64, s::Int64 = -1) # function for creating
original population
if s == -1
X = rand(Bool, ips, nv)
for i = 1:ips
if sum(X[i,:]) == 0
X[i,rand(1:nv)] = true
end
end
else
x = falses(nv)
for i = 1:s; x[i] = true; end
X = Array{Bool}(undef, ips, nv)
for i = 1:ips
X[i,:] = x[randperm(nv)]
end
end
return X
end
function runga(ff::Function, nv::Int64,
ips::Int64 = nv, s::Int64 = div(nv, 2),
ng::Int64 = 1000, pm::Float64 = 0.01,
pc::Float64 = 0.9, pr::Float64 = 0.1) # wrapper
function

X = GeneratePopulation(ips, nv, s)
y = Array{Float64}(undef, ips)
for i = 1:ips
y[i] = evaluation(ff, X[i,:]) # fitness
scores of population
end
n = round(Int64, ips*pr) # elite size
X_ = Array{Bool}(undef, ips, nv) # offspring
population
y_ = Array{Float64}(undef, ips) # fitness
scores of offspring population
for i = 1:ng
X_[1:n, :], y_[1:n] = elitism(X, y, n)
for j = (n+1):ips
xs, ys = selection(X, y, nv, ips)
z, w, new1 = crossover(xs, ys, pc,
nv)
z, new2 = mutation(z, pm, nv)
if new1 || new2
y_new = evaluation(ff, z)
else
y_new = w
end
X_[j,:] = copy(z)
y_[j] = y_new[1]
end
X = copy(X_)
y = copy(y_)
end
ind = findmax(y)[2]
return X[ind, :], y[ind]
end

ГА в действии

Теперь давайте рассмотрим пару ГА в действии. Перед набором кода убедитесь, что вы загрузили пакеты Random и Statistics из базового пакета, так как их функции будут использоваться в этих примерах. Вы можете сделать это следующим образом:

using Random, Statistics

Мы рассмотрим две задачи, используя фреймворк оптимизации ГА. Первая задача поможет вам разобраться в методе, используя пример, с которым вы, возможно, уже сталкивались. Второй пример больше связан с областью науки о данных, поэтому мы будем использовать для него наш второй синтетический набор данных.

Для начала, давайте рассмотрим старую головоломку, связанную с геометрией. Мы выбрали эту «задачу со спичками», так как она проста для понимания, но в то же время достаточно сложна, чтобы иметь неочевидные решения. Цель — сформировать два квадрата, ограничивая общее количество используемых спичек максимум 8. В первом примере мы ищем задачу максимизации. Итак, имея набор из 8 спичек, каково наилучшее расположение, чтобы у нас было два квадрата в сетке 2х2 Рисунок 7

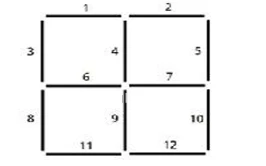
Рисунок 7: Схема кодирования для задачи со спичками в сетке 2x2. 12 линий на этой диаграмме представляют все возможные положения спички.

Сначала мы должны определить правильную функцию приспособленности. Это может показаться немного пугающей задачей, поэтому давайте разобьем ее на более мелкие подзадачи, каждая со своей функцией. (В любом случае, это одна из сильных сторон функционального языка программирования). Этот процесс может показаться немного утомительным сначала, но, по крайней мере, это хорошая практика для развития ваших аналитических навыков (которые весьма передаваемы на другие аспекты ИИ и науки о данных).

весьма переносимы на другие аспекты ИИ и науки о данных).

Начнем с определения всех возможных квадратов по отношению к индексам спичек на основе приведенной выше сетки:

global S = [[1, 3, 4, 6], [2, 4, 5, 7], [6, 8, 9,
11], [7, 9, 10, 12], [1, 2, 3, 5, 8, 10, 11,
12]];

Затем мы можем создать функцию, которая показывает, корректна ли сумма истинных значений в хромосоме:

IsSumRight(x::Array{Bool, 1}, n::Int64) = (sum(x)
== n)

В данном случае n будет равно 8. Однако, хорошая практика сделать эти функции параметрическими, чтобы вы могли экспериментировать с вариантами задачи впоследствии, если потребуется.

Далее нам понадобится создать функцию, которая вычисляет количество квадратов, образованных спичками из данной хромосомы. Это будет выглядеть примерно так:

function NumberOfSquares(x::Array{Bool, 1})
z = 0
for s in S
q = true
for i in s
q = q && x[i]
end
if q; z += 1; end
end
return z
end

Кроме того, нам понадобится функция, которая поможет нам расшифровать хромосому, превращая ее

1s и 0s в индексы, которые мы можем интерпретировать с помощью сетки:

function MatchIndexes(X::Array{Bool, 1})
q = collect(1:12) .* X
return q[q .> 0]
end

Теперь пришло время для фактической функции приспособленности, которая использует все вышеупомянутые вспомогательные функции таким образом, который осмыслен для рассматриваемой задачи:

function ff1(x::Array{Bool, 1})
z = 2.0 # fitness score
if IsSumRight(x, 8)
z += 1
Q = MatchIndexes(x)
OK = true
for q in Q
ok = false
for s in S
if q in s
ok_ = true
for s_ in s
if !(s_ in Q)
ok_ = false
break
end
end
if ok_; ok = true; end
end
end
if !ok
OK = false
end
end
if !OK; z -= 1.5; end # loose ends in the
squares formation
s = NumberOfSquares(x)

if s == 2 # have needed number of squares
z += 1.0
elseif s == 1 # have just one square
z += 0.75
end
end
return z
end

Эта функция может показаться немного сложной, потому что она также сканирует на наличие незакрепленных спичек, что наказывается, поскольку они не являются частью желаемого решения (т.е. их использование упростило бы задачу).

Естественно, нам нужно максимизировать эту функцию. Мы присваиваем значения, которые присваиваем показателю приспособленности хромосомы для различных состояний, потому что даже субоптимальное решение должно быть как-то вознаграждено. В противном случае оптимизатору было бы гораздо труднее понять, движется ли он в правильном направлении, поскольку он смог бы различать только отличное решение и ужасное. Однако, с промежуточными вознаграждениями за решения, которые приемлемы (в правильном направлении), но все еще не идеальны, весь ландшафт решений становится более гладким и легким для навигации алгоритма. Кроме того, важно избегать использования экстремальных значений, таких как Inf или NaN, в качестве части функции приспособленности, так как это сбило бы с толку всю систему во время процесса отбора.

Запуск алгоритма ГА для этой задачи должен быть прямолинейным на этом этапе, хотя для такой задачи лучше использовать больше поколений, чем по умолчанию (по крайней мере 2500):

x, f = runga(ff1, 12, 12, 8, 25000)
println(MatchIndexes(x))
println(f)

Существует два возможных решения этой задачи (которые также симметричны), и система правильно определяет одно из них: [2, 4, 5, 6, 7, 8, 9, 11]. Это соответствует конфигурации, показанной на
Рисунке 8

Рисунок 8. Одно из двух потенциальных решений задачи со спичками, описанной в примере 1. Другое решение представляет собой симметричное изображение этого.

Это решение имеет показатель приспособленности 4.0, что является максимально возможным значением. Обратите внимание, что для получения этого решения, возможно, потребуется запустить оптимизатор пару раз, поскольку он не всегда сходится к нему. Альтернативно, он может сойтись к симметричному расположению, также имеющему показатель приспособленности 4.0.

В качестве второго примера фреймворка ГА мы рассмотрим простую задачу из области науки о данных, связанную с инженерией данных. Имея набор из 40 признаков, мы выясним 20 признаков, которые наименее коррелированы друг с другом. В этом случае мы будем использовать второй набор данных (состоящий из 20 признаков) вместе с набором новых признаков, производных от исходных 20 признаков, используя оператор квадратного корня. Как вы можете ожидать, эти 20 новых признаков сильно коррелированы с исходными 20 признаками, поэтому 20 признаков из окончательного набора признаков должны быть удалены в ходе всего этого процесса.

Начнем с загрузки набора данных:

data = readcsvfile(“data2.csv”);

Обратите внимание, что данные также можно загрузить с помощью функции read() из библиотеки CSV, набрав CSV.read("data2.csv"). Однако пользовательская функция readcsvfile(), использованная здесь, несколько быстрее, поскольку она настроена под конкретную задачу. Мы не будем приводить код для этого метода здесь ради краткости, но вы можете найти его в соответствующем блокноте Jupyter.

Затем нам потребуется выделить признаки набора данных и создать новые

признаки, которые система ГА должна уметь идентифицировать и исключать:

features = data[:, 1:20]
Z = Array{Float64}(undef, 250000, 40)
Z[:, 1:20] = features
for i = 1:20
Z[:, 20 + i] = sqrt.(features[:, i])
end

Очевидно, что новые признаки будут коррелированы с исходными, что мы можем проверить следующим образом:

cor(Z[:,1], Z[:,21])

Однако нам потребуется легкий доступ ко всем корреляциям между различными признаками. Поэтому имеет смысл заранее вычислить все эти корреляции и сохранить их в переменной, доступной всем функциям:

global CM = cor(Z);
for i = 1:40
CM[i,i] = 0.0
end

Обратите внимание, что мы установили корреляцию каждой переменной с самой собой равной 0, чтобы избежать того, чтобы это значение доминировало над всеми остальными.

Теперь пришло время определить функцию приспособленности для этой задачи, которая должна выглядеть примерно так:

function ff2(X::Array{Bool, 1})
N = length(X)
f = collect(1:N) .* X
f = f[f .> 0]
n = length(f)
if n != 20
return -Inf
end

y = Array{Float64}(undef, n)
for i = 1:n
y[i] = (maximum(abs.(CM[f, f])))
end
return -maximum(y)
end

Чтобы найти оптимальный выбор признаков, мы должны убедиться, что в конечном наборе признаков существует только одна версия каждого признака (например, путем удаления всех более новых признаков, или всех более старых, или некоторой комбинации обоих, так что для каждого из исходных признаков в сокращенном наборе признаков остается только одна версия). Таким образом, нам потребуется сделать окончательный результат функции приспособленности отрицательным; это делает весь процесс задачей минимизации. Сделав это, мы можем теперь запустить оптимизатор ГА следующим образом:

x, f = runga(ff2, 40)

Для лучшего понимания результатов мы можем провести некоторую обработку:

ind = collect(1:40) .* x
println(ind[ind .> 0])
println(f)

В этом случае выходными данными являются [1, 2, 3, 4, 5, 6, 7, 8, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 29, 30] и -0.00505, соответствующие индексам выбранных признаков и соответствующей (отрицательной) максимальной абсолютной корреляции между ними. Хотя это не тот результат, который мы ожидали, это имеет смысл; в двух случаях исходные признаки были заменены синтетическими. Тем не менее, общий результат идеально приемлем, поскольку в оптимизированном результате нет дублирующихся признаков. Обратите внимание, что из-за присущей алгоритму ГА случайности вы неизбежно получите немного отличающиеся результаты. Однако они должны давать показатель приспособленности, аналогичный полученному здесь.

Надеюсь, эти примеры продемонстрировали, что нужно проявлять особую

внимательность при кодировании модели ГА. В отличие от других систем ИИ этого класса, ГА не всегда просты в создании функции приспособленности и соответствующем кодировании параметров задачи. Многие ГА требуют кодирования дополнительных функций для практического применения.

Помимо этих примеров, существует множество применений ГА, которые делают их изучение стоящим усилием. Многие из этих случаев часто называют задачей о рюкзаке, которая включает поиск оптимального набора предметов для помещения в рюкзак с учетом некоторых ограничений по весу и некоторой ценности для каждого предмета. Идея заключается в максимизации общей ценности набора, при этом сохраняя общий вес ниже заданного порога для каждого контейнера (рюкзака). Однако другие типы задач, включая оптимизацию непрерывных переменных, также могут быть решены с использованием ГА.

Например, ГА могут использоваться для отбора признаков в качестве методологии уменьшения размерности. Ограничение в этом случае заключалось бы в том, что выбранные признаки составляют менее определенной доли исходного набора признаков, при этом одновременно захватывая как можно больше информации из исходного набора признаков. Естественно, в случаях с большим количеством признаков выбор хорошего подмножества этих признаков может быть довольно сложным из-за огромного количества возможных комбинаций — именно здесь ГА очень пригождаются.

Кроме того, ГА могут использоваться в любых ситуациях, где требуется дискретная оптимизация, например, в нелинейных динамических системах. Одним из таких случаев является фондовый рынок, где ГА могут использоваться для выбора лучших акций для портфеля. Естественно, построение портфеля таким образом потребует дополнительного анализа для определения стоимости каждой акции, но ГА могут играть важную роль в самом процессе отбора, как только эти стоимости будут установлены.

ГА также могут использоваться в других сценариях оптимизации, таких как планирование. Построение оптимального расписания с учетом множества ограничений и предпочтений — это классическая задача дискретной оптимизации, применимая почти везде, от управления проектами до логистики. Пока задача правильно закодирована, ГА могут быть очень эффективны в поиске решения.

Применение, более близкое к науке о данных, — это использование ГА для разработки ANN, как с точки зрения архитектуры, так и с точки зрения весов (обучения). Хотя PSO отлично справляется с определением значений весов, он не очень подходит для работы над архитектурой ANN. Как мы видели в первых главах этой книги,

этой книги, архитектура такой сети включает количество нейронов в каждом слое, а также то, как они связаны (и не все ANN имеют плотную связность).

Наконец, ГА используются в биологических исследованиях, как в случае нахождения формы молекулы белка. Это особенно полезно для исследования потенциальных методов лечения рака, поскольку тесно связанная проблема сворачивания белка является NP-трудной задачей с огромным пространством решений.

Существует еще несколько применений, помимо перечисленных, некоторые из которых более специализированы, чем другие. Тот факт, что ГА находят применение в таком широком спектре областей, свидетельствует об их универсальности и ценности.

Основные варианты ГА

ГА — это очень общий фреймворк, поэтому стандартный алгоритм, который мы видели ранее, имеет несколько вариантов, которые в ряде случаев работают лучше.

Один из таких вариантов — гибридные генетические алгоритмы (HGA), которые по сути представляют собой ансамблевый подход к ГА, выполняемый последовательно (мы подробно рассмотрим ансамбли оптимизации, связанные с PSO, в главе 10). Стандартный ГА сочетается с другим оптимизатором, который лучше подходит для нахождения оптимума в меньшем пространстве решений, обычно используя производные или любую другую дополнительную информацию о функции приспособленности. ГА применяется глобально, и после нахождения локального оптимума другой оптимизатор берет на себя задачу уточнения решения. HGA полезны, когда функция приспособленности может быть дифференцируема, или когда требуется более точное решение.

Еще одним интересным вариантом является самоорганизующийся генетический алгоритм (SOGA). Как следует из названия, SOGA включает процесс, при котором параметры метода оптимизации также оптимизируются вместе с переменными решаемой задачи. Таким образом, вместо тонкой настройки модели оптимизации самостоятельно, модель делает это за вас.

Модель с переменным избирательным давлением (VSPM) — это более новый вариант ГА, заслуживающий внимания. Этот относительно сложный подход к ГА включает изменение стратегии отбора таким образом, чтобы вы могли управлять степенью разнообразия популяции, тем самым избегая чрезмерно однородных или чрезмерно разнообразных популяций. Идея заключается во введении коэффициента «младенческой смертности», который

ограничивает присутствие более слабых хромосом в популяции.

Генетическое программирование

Более того, генетическое программирование (ГП) — мощный вариант ГА, ориентированный на непрерывные переменные. Поскольку он значительно отличается от стандартного ГА и его полезность в приложениях науки о данных заслуживает внимания, мы рассмотрим ГП поближе.

Наконец, любое дополнение к стандартному ГА, такое как процесс элитизма, можно рассматривать как своего рода вариант. В конце концов, широкий фреймворк позволяет вносить изменения, поэтому, если вы немного углубитесь в него, вы наверняка сможете придумать свой собственный вариант метода оптимизации.

Генетическое программирование — интересный вариант ГА, получивший большое внимание в последние годы. Он включает в себя «построение» синтетической функции из других более простых функций, имеющих форму генов. Однако, есть и некоторые данные, которые используются в этих функциях, поэтому входные данные модели ГП включают пару потоков данных, один для входных данных и один для выходных данных функции, которую необходимо аппроксимировать.

Обратите внимание, что эта задача может быть решена с помощью модели регрессии, хотя успех модели будет ограничен линейными комбинациями. Конечно, вы можете использовать нелинейную модель регрессии, но вам придется самостоятельно создавать нелинейные признаки (что требует значительных усилий). Вы также можете использовать ANN, но не сможете увидеть, как входные данные отображаются на выходные (так же, как проблема «черного ящика», которую мы обсуждали в предыдущих главах). Если вам требуется отображение через функцию, которую вы можете видеть целиком, ГП — лучший вариант.

Однако функция, которую генерирует ГП, не обязательно является хорошей моделью, поскольку она обязательно переобучается, если использовать ошибку в качестве функции приспособленности (которую вы будете минимизировать впоследствии). Вот почему более разумно использовать некоторую эвристику, например, коэффициент корреляции или метрику сходства в целом, в качестве функции приспособленности (которую вы будете максимизировать в этом случае). Такие задачи успешно решаются для сценариев слияния признаков как часть модели прогнозной аналитики.15

Функции, которые использует ГП, могут быть любыми: от простого полинома до некоторой сложной тригонометрической функции. Они должны быть в своей самой базовой форме, поскольку более сложные функции неизбежно возникают в процессе

эволюции системы ГП. Например, если у вас есть функции tan(x), x² и x³, то в определенный момент ГП будет иметь хромосомы, состоящие из tan(x²), tan(x³), (tan(x))², x⁶ и т. д. Вот почему при выборе этих функций, которые используются с данными, которые имеют смысл, следует проявлять особую осторожность. Например, нет смысла использовать sqrt(x), если у вас есть точки данных с отрицательным x, хотя sqrt(abs(x)) можно использовать вместо этого.

ГП — это действительно изобретательный метод, который часто добавляет большую ценность, чем обычные варианты ГА, открывая новые возможности. Помимо слияния признаков, он использовался для создания программ на языке LISP. Не позволяйте тому факту, что многие эксперты в области ИИ не знают о ГП, отпугнуть вас от его использования.

Советы по фреймворку ГА

Хотя ГА полезны, они не так просты; вы должны быть осведомлены о нескольких соображениях. Во-первых, поскольку у ГА много параметров, некоторая тонкая настройка обычно необходима. Иногда правильная настройка ГА является большой частью его эффективности, особенно в сложных задачах.

Кроме того, несмотря на то, что ГА способны обрабатывать задачи непрерывной оптимизации, они, как правило, не так эффективны в таких ситуациях. Вот почему, если вы хотите решать такие задачи, вам следует использовать какой-то другой фреймворк оптимизации или специализированный вариант ГА, такой как ГП.

Более того, стандартный ГА не так надежен по сравнению с его вариантами. Поэтому, если вы собираетесь использовать фреймворк ГА для сложной задачи, лучше изучить различные дополнения алгоритма, чтобы получить более эффективную и более производительную систему оптимизации.

Кроме того, как и PSO, ГА отлично подходят, если ваша функция приспособленности не может быть дифференцирована, или процесс дифференцирования очень дорог вычислительно. Однако, если у вас есть легкий доступ к производным функции приспособленности, другие методы оптимизации могут быть более эффективны для нахождения точного решения.

Резюме

• Генетический алгоритм (или ГА) — это эволюционные вычисления.

• фреймворк. Эти алгоритмы имитируют биологию генетического размножения для моделирования задач оптимизации. Здесь хромосомы представляют потенциальные решения.
• Основная часть всех хромосом называется геномом, и он прогрессирует с точки зрения приспособленности в течение нескольких итераций, называемых поколениями.
• ГА включают два основных процесса для развития решений, приближающих их к оптимуму. Это мутация и кроссовер.
• Мутация — это процесс, согласно которому в любом данном поколении хромосома может случайным образом изменить значение гена, переворачивая его. Мутация гарантирует, что геном не будет стагнировать, и поэтому решения не будут ограничены определенной частью поискового пространства.
• Кроссинговер — это процесс, в ходе которого две хромосомы А и В объединяются, образуя две другие хромосомы, каждая из которых состоит из части А и части В. Разделение родительских хромосом может происходить либо в случайном, либо в предопределенном месте. Кроссинговер гарантирует, что решения являются динамическими и, следовательно, способны развиваться со временем.
• Наиболее эффективная хромосома (или хромосомы) иногда сохраняется в следующем поколении. Это гарантирует, что наилучшее решение не ухудшается при неблагоприятных кроссинговерах, мутациях или отборах. Этот процесс называется элитизмом.
• Оригинальный генетический алгоритм включает создание популяции хромосом, их оценку с помощью функции приспособленности, стохастический отбор некоторых из них на основе их показателей приспособленности, применение кроссинговера и мутации к ним на основе этого отбора, создание новой популяции на основе результатов и повторение этого процесса заданное количество поколений или до достижения некоторого другого критерия остановки.
• Особое внимание необходимо уделять части кодирования модели ГА, так как это не всегда просто, при этом некоторые дополнительные функции, возможно, придется кодировать.
• Некоторые из основных вариантов ГА включают гибридные ГА, самоорганизующиеся ГА, модели переменного избирательного давления и генетические

• Программирование.
• Генетическое программирование (ГП) — очень полезный вариант ГА. В ГП в качестве хромосом используются различные функции для создания синтетической функции, аппроксимирующей заданное отображение (например, систему регрессии). ГП использовалось для слияния признаков, среди прочих приложений.
• Хотя ГА могут работать с непрерывными переменными (при правильном кодировании), они не так точны, как другие системы ИИ, такие как PSO и имитация отжига.
• ГА идеально подходят для случаев, когда функция приспособленности не может быть дифференцирована, или процесс дифференцирования слишком дорог вычислительно.

https://bit.ly/2qw8gvZ.

К сожалению, ограничения NDA запрещают обсуждать детали таких проблем.