Глава 8: Создание оптимизатора на основе имитации отжига
Последний (но определенно не последний) из всех рассмотренных в этой книге методов оптимизации существует довольно давно. Созданный в 1983 году доктором С. Киркпатриком и его соавторами,16 имитация отжига (SA) стал оптимизатором, опередившим свое время. Хотя некоторые исследователи относят этот оптимизатор к вариантам метода Монте-Карло, разработанному в 1950-х годах, он был официально признан независимым оптимизатором в 1980-х. Он использует концепции, которые появились только в некоторых вариантах PSO и других, более современных оптимизаторах. Кроме того, несмотря на то, что он существует в той или иной форме уже более полувека, популярным он стал только в 1980-х годах, когда начал развиваться вычислительный интеллект.
Подобно роям и генетике, природное явление «отжига» послужило вдохновением для названия этого типа оптимизатора. Отжиг — это термин в термодинамике, относящийся к процессу охлаждения жидкостей, связанному с образованием кристаллов. Имитация отжига применяет эту концепцию к математическим функциям.
В основе процесса отжига, имитируемого методом SA, лежит температура: управляющий параметр всего процесса. Температура начинается с достаточно высокого значения (например, 10 000 градусов), а затем постепенно падает, обычно с геометрической скоростью. В ходе всего этого уровень энергии жидкости также падает, поскольку она постепенно принимает твердую форму. Это представляет значение функции приспособленности, которая обычно минимизируется (хотя максимизация также возможна).
При относительно высокой температуре возможны более значительные изменения в пространстве поиска; это делает исследование большего числа потенциальных решений возможным, по крайней мере, в начале процесса. Как только температура снижается, исследование уменьшается, поскольку метод предпочитает использование
пространства поиска; позже алгоритм предпочитает уточнять найденные решения.
Если отбросить термодинамический контекст, эта стратегия ближе к тому, что делаем мы, люди, решая задачу оптимизации. Сначала мы пытаемся найти «достаточно хорошее» решение, которое может быть грубым, но всё же несколько полезным, а затем пытаемся улучшить это решение, играя с соответствующими параметрами.
Имитация отжига рассматривается как существенное улучшение метода оптимизации «восхождение на холм», который выбирает наилучшее возможное улучшение функции приспособленности в любой данный момент. Примитивный подход «восхождение на холм» может работать для простых функций, но когда пространство поиска становится более сложным, это одна из худших стратегий оптимизации. Говорят, что SA имитирует алгоритм восхождения на холм ближе к концу своего поиска, когда он пытается «нацелиться» на оптимум функции после определения своего окрестности (где пространство поиска более управляемо).
Основное преимущество метода SA заключается в том, что он достаточно устойчив, в том смысле, что он избегает локальных оптимумов (см.
Рисунок 9). Это особенно полезно в случаях, когда пространство решений не является четко определенным, поскольку функция приспособленности довольно сложна. Эта особенность SA, наряду с тем фактом, что он довольно прост, делает его мощным вариантом для оптимизации таких проблем. Кроме того, стандартный алгоритм SA (который мы рассмотрим через мгновение) может быть улучшен другими процедурами, что делает его еще более эффективным.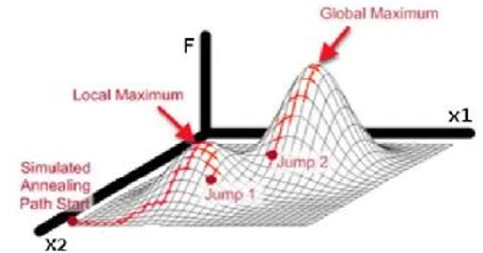
Рисунок 9. Пример поиска максимума с помощью SA, включающий две переменные, x1 и x2. Случайные точки, выбранные в окрестности наилучшего решения в заданное время, называемые «прыжками», выполняются с помощью оптимизатора в попытке опробовать новые решения при относительно высокой температуре. Это приводит к тому, что SA может избежать локальных оптимумов, как локальный максимум в данном случае, и в конечном итоге сойтись к глобальному оптимуму. Изображение основано на оригинале, созданном Максом Дамма (www.maxdama.com).
Недостатком SA является в основном тонкая настройка параметров. Хотя большинство алгоритмов оптимизации имеют набор значений по умолчанию для этих параметров, SA не имеет; нет никаких «эмпирических правил», которые бы обычно работали. Исходную температуру особенно сложно определить. Скорость ее падения также является предметом споров и может сильно варьироваться от задачи к задаче. Таким образом, даже если SA может довольно быстро сходиться, время вычислений может быть долгим (если не настроено правильно), поскольку поиск медленно «остывает» до решения.
Для получения дополнительной информации о SA, с более формализованной точки зрения, вы можете ознакомиться со статьей «Simulated Annealing» профессоров Д. Берцимаса и Дж. Цициклиса, опубликованной в журнале Statistical Science в 1993 году.17
Псевдокод стандартного алгоритма имитации отжига
Теперь давайте рассмотрим шаги стандартного алгоритма SA. Вкратце, процесс выглядит следующим образом:
- Определение режима оптимизации (минимизация или максимизация), начальной температуры, скорости уменьшения температуры, радиуса окрестности для каждой переменной и начального вектора решения.
- Предложение обновленного решения в той же окрестности и его оценка с использованием функции приспособленности.
- Принятие обновлений, улучшающих текущее решение.
- Принятие некоторых обновлений, которые не улучшают текущее решение. Эта «вероятность принятия» зависит от параметра температуры.
- Снижение температуры.
- Повторение шагов 2-5 до тех пор, пока температура не достигнет нуля или заранее заданного минимального значения.
- Вывод найденного наилучшего решения.
Во время итераций важно иметь в виду следующие моменты:
- При выборе нового обновления для решения, вам сначала нужно случайным образом выбрать точку данных в пространстве поиска (представляющую потенциальное решение) из предопределенной области окрестности.
- Новое решение не обязательно может быть лучше, так как существует вероятность того, что произойдет субоптимальное обновление, основанное на температуре.
- Охлаждение, как правило, геометрическое; оно включает параметр охлаждения β, который обычно принимает значения от 0.8 до 0.99. Чем выше β, тем медленнее охлаждение. На k-й итерации температура равна Tk = βTk-1. Если используется такая стратегия охлаждения, убедитесь, что у вас есть
- положительное ненулевое значение для минимальной температуры, чтобы гарантировать, что поиск в конечном итоге «остынет».
- Вероятность принятия p = exp(- ΔC / T), где ΔC — разница в значениях функции приспособленности между текущим и предыдущим решениями, а T — температура в данный момент времени.
- Если охлаждение достаточно медленное, то глобальный оптимум будет достигнут в конечном итоге. Однако это неизбежно займет некоторое время.
Реализация имитации отжига в Julia
Теперь давайте посмотрим, как мы можем реализовать практическую версию SA в Julia. Мы можем начать с некоторых вспомогательных функций:
function sample_ff(x::Array{<:Real, 1},
c::Array{Int64, 1} = ones(Int64, length(x))) #
function to maximize
z = abs.(x) .* c
return 1 / (1 + sum(z))
end
function SelectNeighbor(x::Array{<:Real, 1},
nv::Int64, r::Array{Float64, 1} = ones(nv))
y = Array{eltype(x)}(undef, nv)
for i = 1:nv
y[i] = x[i] + (1 - 2*rand())*r[i]
end
return y
end
function ChancePick(absDE::Float64, T::Float64)
z = exp(absDE / T)
return rand() < z
end
Обратите внимание, что функция sample_ff() не является обязательной, но полезно иметь функцию приспособленности для тестирования алгоритма, чтобы убедиться, что он работает.
должным образом. Также функция соседства не совсем необходима как независимая функция. Однако, поскольку это слабое место алгоритма SA (и оно не было должным образом объяснено ни в одном из источников алгоритма, которые мы нашли), было бы лучше иметь ее как вспомогательную функцию, чтобы мы могли исследовать ее подробнее. В конце концов, в задаче оптимизации не все переменные имеют одинаковый масштаб. Полезно иметь разные варианты радиуса для окрестности каждой переменной, что возможно через функцию SelectNeighbor() и ее параметр r.
После всего этого мы можем перейти к самому алгоритму SA, который можно закодировать следующим образом:
function SA(ff::Function, nv::Int64,
maximize::Bool = true, x::Array{<:Real, 1} =
rand(nv), T::Float64 = 1e4, beta::Float64 = 0.9,
Tmin::Float64 = 1e-9, r::Array{Float64, 1} =
0.5*ones(nv))
x = map(Float64, x)
E = ff(x)
E_best = E
x_best = copy(x)
while T > Tmin
x_n = SelectNeighbor(x, nv, r)
E_n = ff(x_n)
DE = E_n - E
if (maximize && DE >= 0)||(!maximize &&
DE <= 0)
x = copy(x_n)
E = E_n
elseif ChancePick(abs(DE), T)
x = copy(x)
E = E_n
end
if (maximize && (E > E_best))||(!maximize
&& (E < E_best))
E_best = E
x_best = x
end
T *= beta
end return x_best, E_best end
Обратите внимание, что в этой реализации метода SA мы сохраняем запись о наилучшем найденном решении. Этого не было в оригинальном алгоритме, возможно, потому что в то время, когда появился алгоритм SA, люди не до конца понимали, как ведут себя стохастические алгоритмы поиска, и ошибочно предполагали, что эти алгоритмы всегда стремятся к улучшенному решению. Другие реализации оптимизатора SA поддерживают аналогичную стратегию сохранения записи о наилучшем решении, поскольку без этого дополнения алгоритм SA не работал бы так хорошо.
Если вы предпочитаете более устоявшийся пакет для фреймворка SA, вы также можете использовать пакет Optim.jl, который хорошо поддерживается и охватывает различные системы оптимизации в Julia. У него также приличная документация для алгоритмов, которые он включает. В частности, для SA вы можете использовать функцию SimulatedAnnealing(), описанную в такой документации.18
Имитация отжига в действии
Имитация отжига (SA) имеет множество применений, обычно включающих сложные задачи. Классическое применение — обход графа, как в случае задачи коммивояжера. Эта простая задача быстро масштабируется по сложности с увеличением числа узлов в графе, что затрудняет ее решение традиционными оптимизаторами. На данный момент SA и ГА являются лучшими практическими методами ее решения.
SA также используется в области биоинформатики, включая дизайн молекул белка для 3D-представлений. Это NP-трудная задача, имеющая те же вычислительные сложности, что и задача коммивояжера, поэтому она обычно решается с помощью продвинутых методов оптимизации.
Приложения SA также включают проектирование печатных плат, а также логистику в робототехнике. Оба типа задач особенно сложны и не могут быть эффективно решены стандартными оптимизаторами. Также, для задач логистики, время нахождения решения имеет решающее значение; поэтому часто предпочтительны методы оптимизации, такие как SA.
Помимо этих областей, SA имеет приложения во всех областях, связанных с задачами с комплексными пространствами поиска, имеющими различные локальные оптимумы. В таких сценариях большинство распространенных оптимизаторов работают плохо или занимают слишком много времени для сходимости, что делает алгоритмы, подобные SA, наиболее практическими из доступных вариантов.
Давайте теперь рассмотрим, как работает эта программа SA на практике, на паре примеров минимизации и максимизации.
В первом примере мы используем довольно простую функцию, которую будем пытаться оптимизировать с помощью SA. А именно, функция ff1 с четырьмя переменными, состоящая из двух косинусов и объединенного абсолютного значения, имеющая следующую форму:
ff1(x::Array{<:Real, 1}) = (cos(x[1]) + 2)*
(cos(x[2]) + 3) + abs(x[3]*x[4])
Эта функция имеет глобальный минимум 2.0 для решений [π, π, 0, R] и [π, π, R, 0], где R — любое действительное число. Однако из-за характера пространства поиска эти две группы решений не так очевидны — по крайней мере, для алгоритма оптимизации. Для этой задачи мы начнем с потенциального решения x = [2, 4, 1, -1], которое имеет значение 4.716. Это довольно плохо, но мы не хотим слишком облегчать задачу для алгоритма! Сделав это, мы получим лучшее представление о том, как работает оптимизатор. В противном случае, если мы дадим ему случайное решение, это может слишком облегчить задачу, вводя в заблуждение относительно производительности алгоритма.
Запуск функции SA на этих данных довольно прост:
SA(ff1, 4, false, x)
Это дает решение и соответствующее значение функции приспособленности [3.13373, 3.10918, 0.0130858, -0.683512], 2.00953, что совсем неплохо. Последняя переменная (x4) в этом сценарии несущественна (поскольку она охватывается переменной x3 в функции приспособленности), в то время как все остальные, которые вносят вклад в решение, довольно близки к фактическому минимуму, которого алгоритм пытался достичь.
Второй пример рассматривает столь же сложную функцию, включающую пару тригонометрических выражений, а также простой полином. Эта функция, которую мы назовем ff2, принимает в Julia следующую форму:
ff2(x::Array{<:Real, 1}) = -x[1]^2 + 2 / (1 +
abs(tan(x[2]))) - cos(x[3])
Естественно, он имеет глобальный максимум 3.0, соответствующий решению [0, 0, π]. Поскольку мы хотим довести алгоритм до его предела, мы начнем с потенциального решения x = [1, -1, 2], которое соответствует довольно ужасному показателю приспособленности около 0.198. Теперь используем функцию SA, чтобы увидеть, как это решение может быть улучшено. Для этой задачи она принимает форму:
SA(ff2, 3, true, x)
Полученное решение: [0.0731461, -0.00582237, 2.93553], соответствующее значение приспособленности 2.96192 — значительное улучшение и довольно близко к глобальному максимуму.
Основные варианты имитации отжига
В отличие от других систем оптимизации, SA не имеет много вариантов. Здесь описаны три основных типа:
- Детерминированная SA. Хотя SA по своей природе является стохастическим, существует его вариант, который является детерминированным. Ключевое преимущество в том, что он быстрее стандартного метода SA. Однако он не может гарантировать оптимальное решение проблемы, которую решает. Детерминированная SA применялась к задачам кластеризации, в частности к подходу Fuzzy C-means, альтернативе хорошо известного алгоритма K-means, использующего нечеткую логику.
19 - Адаптивная SA. Этот вариант решает проблему наличия слишком многих параметров для настройки, используя эвристики для управления расписанием температуры. Это делает этот вариант более эффективным, чем стандартный алгоритм SA, и несколько проще в использовании. Адаптивная SA также имеет версию для параллельной обработки, которая еще более эффективна.
- Квантовый отжиг. Это несколько иной подход.
ко всей проблеме, хотя он заимствует все ключевые элементы стандартного алгоритма SA. Основное различие заключается в том, что квантовый отжиг использует «квантовые флуктуации» (вместо тепловых флуктуаций) для обхода нерегулярных областей в ландшафте пространства поиска по отношению к функции приспособленности. Обратите внимание, что физический процесс квантового отжига используется в квантовых компьютерах D-Wave и делает их «квантовыми», хотя другие квантовые свойства также могут использоваться в обычном компьютере.
Советы по оптимизатору имитации отжига
Несмотря на то, что фреймворк оптимизации SA тщательно тестировался в течение нескольких лет, все еще есть вещи, которые следует иметь в виду. В отличие от большинства современных оптимизаторов, SA не был создан с учетом практичности; как таковой, для его хорошей работы требуется много тонкой настройки. Если вы планируете использовать этот подход к оптимизации, убедитесь, что вы правильно его настроили, прежде чем принимать предложенное решение как истину.
Иногда, охотясь за хорошим решением, как собака за дичью, SA может сойти с тропы и не найти ничего ценного. Если это произойдет, вы можете реализовать дополнение под названием «перезапуск», при котором система может принять решение вернуться к значительно лучшему решению, если решения, к которым она склоняется, не лучше. Существует несколько факторов, которые следует учитывать перед выполнением «перезапуска». Это неизбежно замедляет поиск, поэтому убедитесь, что вы хорошо знаете алгоритм, прежде чем реализовывать такое напряженное дополнение.
Наконец, лучше всего начинать с высоких температур при использовании SA, поскольку это гарантированно даст хорошее решение. Если алгоритм работает слишком долго, вы всегда можете увеличить скорость охлаждения или начать с более низкой температуры. В любом случае, помните об этом компромиссе между эффективностью и скоростью в алгоритме SA.
Резюме
- Имитация отжига (SA) — простой, надежный и эффективный алгоритм оптимизации.
- SA имитирует процесс охлаждения жидкостей при образовании кристаллов для оптимизации всего процесса поиска. При высокой температуре SA фокусируется на исследовании большей части пространства решений; по мере «остывания» он фокусируется на уточнении уже найденных решений. Таким образом, он обычно избегает застревания в локальных оптимумах.
- Стандартный алгоритм SA может гарантировать оптимальное решение, если скорость охлаждения достаточно низкая.
- Несколько вариантов SA включают детерминированную SA, адаптивную SA и квантовый отжиг. Каждый из этих методов имеет уникальные преимущества перед основным алгоритмом SA.
- Существуют различные применения SA, такие как обход графа, биоинформатика, проектирование печатных плат и логистика для робототехники. SA особенно хорошо подходит для решения задач класса «NP», которые имеют различные оптимумы, что делает их особенно сложными.
- Дополнение «перезапуск» к методу SA, которое позволяет вернуться к «хорошему» решению в случае «схода с неверной тропы» в поиске, может быть полезным. Однако решение о применении перезапуска не является тривиальной задачей.
- SA лучше всего подходит для решения сложных задач с множественными оптимумами, большинство из которых являются локальными оптимумами, значения приспособленности которых не соответствуют требованиям приложения оптимизации, над которым мы работаем.
http://bit.ly/2Oac0fP.
https://bit.ly/2I9fOei.
https://bit.ly/2GdhJBW.
http://bit.ly/2MiIfZM.