Ai for data science

Глава 9: Создание продвинутой системы глубокого обучения

В предыдущих главах мы узнали, как строить модели глубокого обучения с использованием фреймворков MXNet, TensorFlow и Keras. Напомним, что модели, которые мы использовали в тех главах, известны как искусственные нейронные сети, или ANN. Недавние исследования ANN выявили широкий тип нейронных сетей, имеющих специальные архитектуры, отличные от архитектуры ANN.

В этой главе мы представим две наиболее популярные альтернативные архитектуры, которые весьма полезны для задач, таких как классификация изображений и машинный перевод.

Первая модель, которую мы упомянем, — это сверточная нейронная сеть. Эти модели хорошо работают в задачах, связанных с компьютерным зрением; в некоторых областях, таких как распознавание изображений, они уже превзошли человеческую производительность. Вторая модель, которую мы рассмотрим, — это рекуррентная нейронная сеть, которая очень удобна для моделирования последовательностей, включая машинный перевод и распознавание речи. Хотя в этой главе мы ограничимся рассмотрением этих двух типов нейронных сетей, вы можете прочитать больше о других выдающихся сетевых архитектурах в приложениях к этой книге.

Сверточные нейронные сети (CNN)

Одна из самых интересных систем глубокого обучения — это сверточная нейронная сеть (обычно называемая CNN, хотя некоторые используют термин ConvNets). Это сети глубокого обучения, которые очень эффективны в решении задач, связанных с изображениями или звуком, особенно в рамках методологии классификации.

Однако с годами их архитектура развивалась, и их применимость расширилась, включив различные случаи, такие как NLP (обработка естественного языка — обработка и классификация различных человеческих предложений). Кроме того, сверточные слои, используемые в CNN, могут быть интегрированы как компоненты более продвинутых систем глубокого обучения, таких как GAN (см. Приложение D). Начнем с описания архитектуры и строительных блоков CNN.

Компоненты CNN

CNN значительно эволюционировали с момента их появления в 1980-х годах. Однако большинство из них используют некоторую вариацию архитектуры LeNet, представленную Янном ЛеКуном и расцветшую в 1990-х. В то время CNN использовались в основном для задач распознавания символов; эта ниша изменилась, поскольку они стали более универсальными в других областях, таких как обнаружение и сегментация объектов.

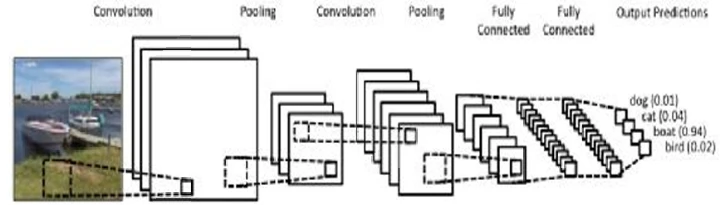
Рисунок 10
показывает простую архитектуру CNN, ориентированную на классификацию изображений. Она состоит из нескольких слоев, каждый из которых специализирован определенным образом. Эти слои в конечном итоге формируют серию мета-признаков, которые затем используются для классификации исходных данных в один из классов, представленных отдельными нейронами на выходном слое. На выходном слое обычно используется функция, такая как сигмоида, для вычисления оценок для каждого класса. Эти оценки могут интерпретироваться как вероятности. Например, если оценка для первого класса равна 0.20, мы можем сказать, что вероятность принадлежности наблюдения к первому классу составляет 20%.

Рисунок 10. Графическое изображение работы CNN, ориентированной на изображения, на основе архитектуры LeNet. Обратите внимание, что каждый нейрон в каждом скрытом слое немного отличается, чтобы лучше обобщать данные в файле изображения. Выходной слой соответствует 4 разным классам этой задачи классификации, с числом с плавающей точкой в соответствующих нейронах, соответствующим вероятности того, что исходное изображение принадлежит к этому конкретному классу. Источник графики: www.clarifai.com.

Поток данных и функциональность

Поток данных в CNN такой же, как и в базовой системе глубокого обучения, такой как MLP. Однако функциональность CNN характеризуется серией ключевых операций, уникальных для этого типа сети глубокого обучения. А именно, функциональность описывается с точки зрения:

1. Свертка
2. Нелинейность (обычно через функцию ReLU, хотя tanh и сигмоида также являются жизнеспособными вариантами)
3. Пулинг (особый вид подвыборки)
4. Классификация через полносвязные слои

Мы рассмотрим каждую из этих операций ниже. Прежде чем это сделать, обратите внимание, что все данные исходного изображения (или аудиоклипа и т. д.) имеют форму серии

целочисленных признаков. В случае изображения каждый из этих признаков соответствует определенному пикселю этого изображения. Однако CNN также может использовать данные датчиков в качестве входных данных, что делает его очень универсальной системой.

Свертка

Именно здесь CNN получили свое название. Идея свертки заключается в извлечении признаков из входного изображения методичным и эффективным образом. Ключевое преимущество этого процесса в том, что он учитывает пространственные отношения между пикселями. Это достигается с помощью небольшого квадрата (также известного как «фильтр»), который проходит по матрице изображения шагами в один пиксель.
Рисунок 11
ниже демонстрирует оператор свертки:

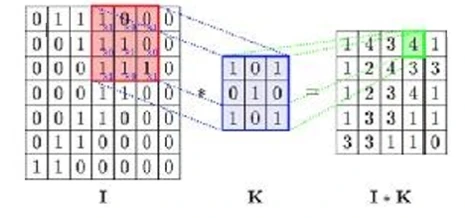
Рисунок 11. Базовая визуализация операции свертки. I - это входная матрица, а K - это фильтровальная матрица. Источник: https://bit.ly/2NTOxfh.

С программной точки зрения, удобно представлять входной сигнал сверточного слоя как двумерную матрицу (представленную как матрица I на
Рисунке 11
). Фактически, операция свертки — это просто серия умножений матриц, где матрица фильтра умножается на сдвинутую часть входной матрицы каждый раз, и элементы полученной матрицы суммируются. Этот простой математический процесс позволяет системе CNN получать информацию о локальных аспектах анализируемых данных, придавая ей смысл контекста, который она может использовать в решаемой задаче науки о данных.

Выход этого процесса представляется серией нейронов, составляющих карту признаков. Обычно используется более одного фильтра для лучшего захвата

тонкости исходного изображения, приводящие к карте признаков с определенной «глубиной» (которая, по сути, является стеком различных слоев, каждый соответствует фильтру).

Нелинейность

Нелинейность необходима во всех системах глубокого обучения, и поскольку свертка является линейной операцией, нам необходимо ввести нелинейность другим способом. Одним из таких способов является функция ReLU, которая применяется к каждому пикселю изображения. Обратите внимание, что могут использоваться и другие нелинейные функции, такие как гиперболический тангенс (tanh) или сигмоида. Описания этих функций приведены в глоссарии.

Пулинг

Поскольку карты признаков и результаты нелинейных преобразований исходных данных довольно велики, в последующей части мы делаем их меньше посредством процесса, называемого пулингом. Это включает некоторую операцию суммирования, такую как взятие максимального значения (называемого «макс-пулинг»), среднего или даже суммы определенной окрестности (например, окна 3х3). Различные эксперименты показали, что макс-пулинг дает наилучшую производительность. Наконец, процесс пулинга является эффективным способом предотвращения переобучения.

Классификация

Эта финальная часть функциональности CNN почти идентична таковой у MLP, который использует softmax в качестве передаточной функции на финальном слое. В качестве входных данных CNN использует мета-признаки, созданные пулингом. Полносвязные слои в этой части CNN позволяют дополнительную нелинейность и различные комбинации этих высокоуровневых признаков, что приводит к лучшему обобщению при относительно низких вычислительных затратах.

Процесс обучения

При обучении CNN мы можем использовать различные алгоритмы; наиболее популярным является обратное распространение ошибки. Естественно, мы должны моделировать выходные данные, используя серию бинарных векторов, размер которых равен количеству классов. Также начальные веса во всех связях и фильтрах являются случайными. После полного обучения CNN его можно использовать для идентификации новых изображений, связанных

к заранее заданным классам.

Визуализация модели CNN

Визуализация CNN часто необходима, так как это позволяет нам лучше понять результаты и решить, правильно ли обучена CNN. Это особенно полезно при работе с данными изображений, поскольку мы можем видеть, как восприятие входного изображения CNN меняется на протяжении различных слоев.
Рисунок 12
показывает пример такой визуализации CNN.

Рисунок 12. Базовая визуализация CNN, использованной для анализа изображения и предсказания того, что изображено на нем. Источник: https://bit.ly/2uBGKOR.

CNN в действии

Теперь давайте посмотрим, как работают CNN с реальной задачей. Здесь мы приведем пример классификации изображений с помощью CNN, используя Python и Keras. В примере мы используем одну из самых популярных баз данных для распознавания изображений — набор данных MNIST. Этот набор данных состоит из рукописных цифр от 0 до 9. Наша задача — определить правильную цифру на изображениях, содержащих рукописные символы.
Рисунок 13
показывает примеры

из набора данных MNIST.

Рисунок 13. Примеры изображений и соответствующие метки из набора данных MNIST. Источник: https://bit.ly/2u0Sl4f.

Мы увидим, что модуль наборов данных Keras уже предоставляет этот набор данных, поэтому дополнительная загрузка не требуется. Приведенный ниже код взят из официального репозитория Keras.20

Как обычно, начинаем с импорта необходимых библиотек. Также импортируем набор данных MNIST из модуля datasets Keras:

from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K

Затем мы определяем размер пакета как 128, количество классов как 10 (количество цифр от 0 до 9), количество эпох для запуска модели как 12, а размерность входного изображения как (28,28), поскольку все соответствующие изображения имеют размер 28 на 28 пикселей:

batch_size = 128
num_classes = 10
epochs = 12
img_rows, img_cols = 28, 28

Затем получаем данные MNIST и загружаем их в переменные, после разбиения на обучающий и тестовый наборы:

(x_train, y_train), (x_test, y_test) =
mnist.load_data()

Пришло время для некоторой предварительной обработки — в основном изменение формы переменных, которые содержат данные:

It is time for some pre-processing—mostly reshaping the variables that
hold the data:
if K.image_data_format() == ‘channels_first’:
x_train = x_train.reshape(x_train.shape[0],
1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1,
img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0],
img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0],
img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype(‘float32’)
x_test = x_test.astype(‘float32’)
x_train /= 255
x_test /= 255
print(‘x_train shape:’, x_train.shape)
print(x_train.shape[0], ‘train samples’)

print(x_test.shape[0], ‘test samples’)

Затем преобразуем векторы, содержащие классы, в бинарные матрицы классов:

y_train = keras.utils.to_categorical(y_train,
num_classes)
y_test = keras.utils.to_categorical(y_test,
num_classes)

После этих шагов мы готовы построить наш граф, используя последовательную модель. Сначала мы добавляем два сверточных слоя друг поверх друга, затем применяем операцию макс-пулинга к выходу второго сверточного слоя. Далее применяем dropout. Прежде чем подать полученный выход в плотный слой, мы разравниваем наши переменные в соответствии с входными формами плотного слоя. Выход этого плотного слоя регулируется dropout; полученный выход затем подается в последний плотный слой для классификации. Функция softmax используется для преобразования результатов в нечто, что может быть интерпретировано в терминах вероятностей. Ниже приведен фрагмент кода построения модели:

model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes,
activation='softmax'))

Далее компилируем нашу модель, используя кросс-энтропийные потери и алгоритм оптимизации Adadelta. В качестве метрики оценки используем точность, как обычно:

model.compile(loss=keras.losses.categorical_cross

entropy,
optimizer=keras.optimizers.Adadelta
(),
metrics=['accuracy'])

Пришло время обучить нашу модель на обучающем наборе, который мы выделили из исходного набора данных MNIST ранее. Мы просто используем функцию fit() объекта модели для обучения нашей модели:

model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))

Наконец, мы оцениваем производительность нашей модели на тестовом наборе:

score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

После 12 эпох наша модель достигает точности почти 99% на тестовом наборе — весьма удовлетворительный результат для такой простой модели. Этот пример демонстрирует, насколько успешны CNN в задачах классификации изображений. Ниже приведен вывод всего кода:

Downloading data from
https://s3.amazonaws.com/img-datasets/mnist.npz
11493376/11490434
[==============================] - 15s 1us/step
x_train shape: (60000, 28, 28, 1)
60000 train samples
10000 test samples
Train on 60000 samples, validate on 10000 samples
Epoch 1/12
60000/60000 [==============================] -
105s 2ms/step - loss: 0.2674 - acc: 0.9184 -
val_loss: 0.0584 - val_acc: 0.9809

Epoch 2/12
60000/60000 [==============================] -
106s 2ms/step - loss: 0.0893 - acc: 0.9734 -
val_loss: 0.0444 - val_acc: 0.9863
Epoch 3/12
60000/60000 [==============================] -
108s 2ms/step - loss: 0.0682 - acc: 0.9798 -
val_loss: 0.0387 - val_acc: 0.9864
Epoch 4/12
60000/60000 [==============================] -
109s 2ms/step - loss: 0.0565 - acc: 0.9835 -
val_loss: 0.0365 - val_acc: 0.9889
Epoch 5/12
60000/60000 [==============================] -
110s 2ms/step - loss: 0.0472 - acc: 0.9860 -
val_loss: 0.0311 - val_acc: 0.9899
Epoch 6/12
60000/60000 [==============================] -
110s 2ms/step - loss: 0.0418 - acc: 0.9878 -
val_loss: 0.0343 - val_acc: 0.9893
Epoch 7/12
60000/60000 [==============================] -
109s 2ms/step - loss: 0.0354 - acc: 0.9895 -
val_loss: 0.0266 - val_acc: 0.9918
Epoch 8/12
60000/60000 [==============================] -
107s 2ms/step - loss: 0.0341 - acc: 0.9897 -
val_loss: 0.0306 - val_acc: 0.9910
Epoch 9/12
60000/60000 [==============================] -
102s 2ms/step - loss: 0.0298 - acc: 0.9907 -
val_loss: 0.0282 - val_acc: 0.9915
Epoch 10/12
60000/60000 [==============================] -
103s 2ms/step - loss: 0.0290 - acc: 0.9911 -
val_loss: 0.0273 - val_acc: 0.9915
Epoch 11/12

60000/60000 [==============================] -
108s 2ms/step - loss: 0.0285 - acc: 0.9911 -
val_loss: 0.0283 - val_acc: 0.9915
Epoch 12/12
60000/60000 [==============================] -
118s 2ms/step - loss: 0.0253 - acc: 0.9920 -
val_loss: 0.0249 - val_acc: 0.9918
Test loss: 0.024864526777043875
Test accuracy: 0.9918

CNN могут использоваться в нескольких различных приложениях:

• Идентификация лиц. Это приложение особенно полезно в задачах анализа изображений. Оно работает, сначала отбрасывая части изображения, не содержащие лица, которые обрабатываются в низком разрешении. Затем оно фокусируется на частях, содержащих лицо, и рисует воспринимаемые границы в высоком разрешении для лучшей точности.21
• Компьютерное зрение (CV) в целом. Помимо распознавания лиц, CNN применяются в различных других сценариях компьютерного зрения. Это была горячая тема в течение последних десяти или около того лет, и она породила множество приложений.22
• Самоуправляемые автомобили. Поскольку CV играет важную роль в самоуправляемых автомобилях, CNN часто является выбранным инструментом ИИ для этой технологии. Их универсальность в отношении типов входных данных и тот факт, что они тщательно изучены, делают их предпочтительным вариантом для проекта самоуправляемого автомобиля NVIDIA, например.23
• NLP. Благодаря высокой скорости и универсальности, CNN хорошо подходят для приложений NLP. Ключ здесь - «перевести» все слова в соответствующие внедрения (embeddings), используя специализированные методы, такие как GloVe или word2vec. CNN оптимальны здесь, поскольку модели NLP варьируются от невероятно простых, таких как «мешок слов», до вычислительно сложных, таких как n-граммы.24

Рекуррентные нейронные сети

Рекуррентные нейронные сети (RNN) — это интересный тип сетей глубокого обучения, широко используемый в приложениях NLP. Они обрабатывают данные последовательно, что приводит к улучшенному анализу сложных наборов данных, благодаря моделированию временного аспекта данных. В некотором смысле RNN имитируют человеческую память; это позволяет им понимать взаимосвязи между точками данных, как и мы.

Интересно, что РНН также могут использоваться для текстового искусственного творчества. Для них характерно генерировать текст, стилистически напоминающий прозу или даже стихи какого-то известного писателя, как мы видели в главе 2. Из-за их популярности у РНН есть несколько вариантов, которые даже более эффективны для задач, в которых они специализируются.

Компоненты RNN

RNN имеют в своем названии слово «рекуррентные» потому, что они выполняют одну и ту же задачу для каждого элемента последовательности, при этом результат зависит от предыдущих вычислений. Это принимает форму петель в архитектуре RNN, как, например, на
Рисунке 14
.

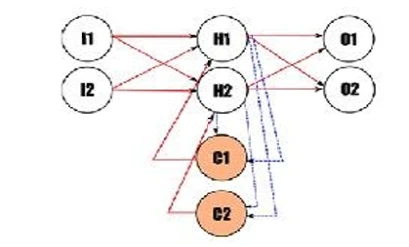
Рисунок 14. Графическое изображение довольно рудиментарной RNN. Обратите внимание на рекуррентные узлы C1 и C2, соответствующие скрытому слою, включающему узлы H1 и H2. Исходное изображение: Tiago Reul.

Эта архитектура могла бы позволить сети учитывать неограниченное количество предыдущих состояний данных. На самом деле, однако, она обычно включает лишь несколько шагов. Этого достаточно, чтобы система RNN получила ощущение «памяти», позволяющее ей видеть каждую точку данных в контексте других точек данных, предшествующих ей.

Поскольку рекуррентные связи в RNN не всегда легко изобразить или понять (особенно при попытке проанализировать поток данных), мы часто «разворачиваем» их. Это создает более развернутую версию той же сети, где временной аспект данных становится более очевидным, как видно на
Рисунке 15
. Этот процесс иногда называют «развертыванием» или «раскрытием».

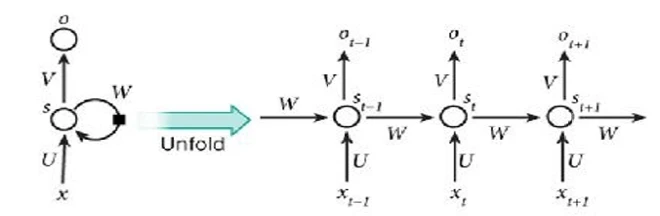
Рисунок 15. Раскрытие RNN, позволяющее лучше видеть поток данных. Источник изображения: Nature

Поток данных и функциональность

Данные в RNN циркулируют в петлях, по мере того как система постепенно учится, как каждая точка данных коррелирует с некоторыми из предыдущих. В этом контексте скрытые узлы RNN (которые часто называют «состояниями») являются по сути памятью системы. Как и следовало ожидать, эти узлы имеют нелинейную функцию активации, такую как ReLU или tanh. Функция активации финального слоя перед выходом обычно имеет функцию softmax, чтобы аппроксимировать вероятности.

В отличие от традиционной системы глубокого обучения, которая использует разные веса на каждом слое, RNN разделяет одни и те же параметры на всех этапах. Это связано с тем, что по сути она выполняет одну и ту же задачу на каждом шаге, отличаясь только входными данными. Это значительно уменьшает общее количество параметров, которые она должна изучить, что делает фазу обучения значительно быстрее и computationally lighter.

Процесс обучения

При обучении RNN мы используем многие из тех же принципов, что и в других сетях глубокого обучения, с ключевым отличием в алгоритме обучения (которым обычно является обратное распространение ошибки). RNN требуют алгоритма, который учитывает количество шагов, которые нам нужно было пройти, прежде чем достигнуть узла при

вычислении градиента ошибки каждого выходного узла. Этот вариант алгоритма обучения называется распространением ошибки по времени (BPTT). Поскольку функция градиента нестабильна при прохождении через RNN, BPTT не очень хорошо помогает RNN учиться долгосрочным зависимостям между его точками данных. К счастью, эта проблема решается с использованием специализированной архитектуры, называемой LSTM, которую мы обсудим в следующем разделе.

Варианты RNN

Что касается вариантов RNN, то выделяются двунаправленные RNN (а также их «глубокая» версия), LSTM и GRU.

Двунаправленные RNN и их более глубокие аналоги

Двунаправленная RNN подобна ансамблю из двух RNN. Ключевое различие между этими двумя сетями заключается в том, что одна из них учитывает предыдущие точки данных, в то время как другая рассматривает последующие точки данных. Таким образом, вместе они могут дать более целостное представление о имеющихся данных, поскольку они знают как то, что было до, так и то, что следует после. Глубокая двунаправленная RNN подобна обычной двунаправленной RNN, но с несколькими слоями для каждого временного шага. Это позволяет делать лучшие предсказания, но требует гораздо большего набора данных.

LSTM и GRU

LSTM (Long Short Term Memory) — это очень уникальный тип RNN (или ячейки), широко используемый в задачах NLP. Он состоит из четырех различных ANN, которые работают вместе, создавая своего рода память, которая не ограничена алгоритмом обучения (как в обычных RNN). Это возможно, потому что LSTM имеют внутренний механизм, который позволяет им выборочно забывать и объединять различные предыдущие состояния, способствуя отображению долгосрочных зависимостей.
Рисунок 16
демонстрирует стандартную ячейку LSTM с тремя вентилями (входным, обновляющим и выходным):

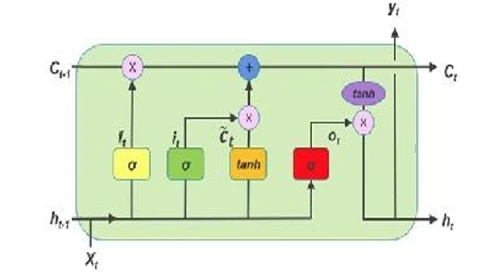
Рисунок 16. На рисунке переменные h представляют кратковременную память, а переменные C — долговременную память. Желтый вентиль — это входной, зеленый вентиль — обновляющий, а красный вентиль — выходной. Источник изображения: https://bit.ly/2uCVBLL.

LSTM довольно сложны; поэтому разработчики быстро искали более простую версию. Здесь вступают в игру GRU, или Gated Recurrent Units; GRU — это по сути легкая версия LSTM. GRU — это сеть LSTM с двумя вентилями — одним для сброса и одним для обновления предыдущих состояний. Первый вентиль определяет, как лучше всего объединить новый вход с предыдущей памятью, в то время как второй вентиль определяет, сколько предыдущей памяти следует сохранить.

РНН в действии

Здесь мы приведем пример классификации текста с использованием варианта РНН - LSTM. Код реализован на Python и Keras. Набор данных, который мы используем, взят из базы данных фильмов IMDB; он уже доступен с модулем наборов данных Keras. Набор данных включает комментарии пользователей IMDB к фильмам и связанные с ними настроения. Наша задача - классифицировать комментарии как положительные или отрицательные настроения - это задача бинарной классификации. Код ниже взят из официального репозитория Keras.25

Сначала, как обычно, импортируем необходимые библиотеки. Обратите внимание, что мы

также импортируем набор данных IMDB из модуля наборов данных Keras:

from __future__ import print_function
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding
from keras.layers import LSTM
from keras.datasets import imdb

Затем мы устанавливаем максимальное количество признаков равным 20 000; максимальное количество слов в тексте — 80; и размер пакета — 32:

max_features = 20000
maxlen = 80
batch_size = 32

Далее загружаем набор данных в некоторые переменные, после разбиения на обучающий и тестовый наборы:

(x_train, y_train), (x_test, y_test) =
imdb.load_data(num_words=max_features)

Нам нужно дополнить некоторые текстовые комментарии, поскольку некоторые из них короче 80 слов, а наша модель принимает только входные данные одинаковой длины. Вкратце, дополнение работает путем добавления предопределенного слова в конец последовательности для достижения желаемой длины. Код ниже дополняет последовательности:

x_train = sequence.pad_sequences(x_train,
maxlen=maxlen)
x_test = sequence.pad_sequences(x_test,
maxlen=maxlen)

Теперь мы полностью готовы построить нашу последовательную модель. Сначала мы добавляем слой встраивания (embedding layer), а затем добавляем LSTM. Наконец, мы добавляем плотный слой для классификации:

model = Sequential()
model.add(Embedding(max_features, 128))

model.add(LSTM(128, dropout=0.2,
recurrent_dropout=0.2))
model.add(Dense(1, activation=‘sigmoid’))

После построения модели мы можем обучать ее на нашем тренировочном наборе. Мы используем бинарную кросс-энтропийную потерю в качестве функции потерь, алгоритм Adam в качестве нашего оптимизатора и точность в качестве метрики оценки:

model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])

Пришло время обучить нашу модель:

model.fit(x_train, y_train,
batch_size=batch_size,
epochs=10,
validation_data=(x_test, y_test))

Наконец, мы тестируем производительность нашей модели на тестовом наборе:

score, acc = model.evaluate(x_test, y_test,
batch_size=batch_size
)
print('Test score:', score)
print('Test accuracy:', acc)

Модель достигает почти 82% точности на тестовом наборе после 10 эпох, что является удовлетворительным результатом для такой простой модели. Вывод кода выше:

Train on 25000 samples, validate on 25000 samples
Epoch 1/10
25000/25000 [==============================] -
91s 4ms/step - loss: 0.4555 - acc: 0.7836 -
val_loss: 0.3905 - val_acc: 0.8279
Epoch 2/10
25000/25000 [==============================] -
90s 4ms/step - loss: 0.2941 - acc: 0.8813 -

val_loss: 0.3796 - val_acc: 0.8316
Epoch 3/10
25000/25000 [==============================] -
94s 4ms/step - loss: 0.2140 - acc: 0.9178 -
val_loss: 0.4177 - val_acc: 0.8311
Epoch 4/10
25000/25000 [==============================] -
96s 4ms/step - loss: 0.1565 - acc: 0.9416 -
val_loss: 0.4811 - val_acc: 0.8238
Epoch 5/10
25000/25000 [==============================] -
96s 4ms/step - loss: 0.1076 - acc: 0.9614 -
val_loss: 0.6152 - val_acc: 0.8150
Epoch 6/10
25000/25000 [==============================] -
92s 4ms/step - loss: 0.0786 - acc: 0.9727 -
val_loss: 0.7031 - val_acc: 0.8225
Epoch 7/10
25000/25000 [==============================] -
91s 4ms/step - loss: 0.0513 - acc: 0.9831 -
val_loss: 0.7056 - val_acc: 0.8166
Epoch 8/10
25000/25000 [==============================] -
91s 4ms/step - loss: 0.0423 - acc: 0.9865 -
val_loss: 0.8886 - val_acc: 0.8112
Epoch 9/10
25000/25000 [==============================] -
91s 4ms/step - loss: 0.0314 - acc: 0.9895 -
val_loss: 0.8625 - val_acc: 0.8140
Epoch 10/10
25000/25000 [==============================] -
91s 4ms/step - loss: 0.0255 - acc: 0.9920 -
val_loss: 1.0046 - val_acc: 0.8152
25000/25000 [==============================] -
14s 563us/step
Test score: 1.0045836124545335
Test accuracy: 0.8152

Перед завершением этой главы мы обратим ваше внимание на несколько других продвинутых моделей глубокого обучения (например, GAN), содержащихся в приложениях к этой книге. Мы настоятельно рекомендуем вам прочитать эти приложения, чтобы узнать больше о моделях глубокого обучения. После этого вы сможете найти множество других полезных ресурсов, чтобы углубиться в детали моделей глубокого обучения.

RNN идеально подходят для решения следующих задач:

• NLP. Как упоминалось ранее, РНН отлично справляются с обработкой текста на естественном языке. Задачи, такие как предсказание следующего слова или определение общей темы блока текста, хорошо решаются РНН.
• Синтез текста. Особое приложение NLP, заслуживающее отдельного пункта, — синтез текста. Оно включает создание новых потоков слов, что является расширением приложения «предсказание следующего слова». РНН могут создавать целые абзацы текста, поднимая предсказание текста на совершенно новый уровень.
• Автоматический перевод. Это более сложная задача, чем кажется, поскольку каждый язык и диалект имеют свои тонкости (например, порядок слов при построении предложения). Для точного перевода чего-либо компьютер должен обрабатывать предложения целиком — что стало возможным благодаря модели RNN.
• Генерация подписей к изображениям. Хотя это не совсем связано с RNN, это, безусловно, полезное приложение. В сочетании с CNN, RNN могут генерировать краткие описания изображений, идеально подходящие для подписей. Они могут даже оценивать и ранжировать наиболее важные части изображения, от наиболее до наименее релевантных.
• Распознавание речи. Когда звук говорящего человека преобразуется в цифровой звуковой сигнал, несложно попросить RNN понять контекст каждого звукового фрагмента. Следующий шаг — преобразование этого в письменный текст, что довольно сложно, но возможно с использованием той же технологии RNN.

Резюме

• Сверточные нейронные сети (CNN) и рекуррентные нейронные сети (RNN) — две наиболее популярные архитектуры нейронных сетей, помимо ANN. CNN очень хорошо справляются с задачами, связанными с изображениями, такими как распознавание изображений и генерация подписей, а RNN довольно эффективны в последовательных задачах, таких как машинный перевод.
• CNN достигают передовой производительности в некоторых задачах компьютерного зрения и даже превзошли производительность человека.
• РНН очень подходят для задач, которые могут быть представлены в виде последовательностей.
• Существует множество вариантов RNN. Два наиболее популярных — LSTM и GRU. LSTM состоят из четырех вентилей, а GRU — из двух вентилей. В этом отношении GRU — облегченные версии LSTM.

https://bit.ly/2qfAjPM.

http://bit.ly/2o175Da.

http://bit.ly/2o5B63Y.

http://bit.ly/2Hfxky2.

http://bit.ly/21HCl4h.

https://bit.ly/2FuKCog.