Глава 10: Создание ансамбля оптимизации
Ансамбли, как правило, полезны, когда речь заходит о системах науки о данных, поскольку они объединяют лучшие черты различных методов. Подобно тому, как любая машина больше, чем сумма ее частей, эти сложные ансамбли работают лучше, чем их отдельные компоненты. Цель любого ансамбля — получить лучший результат, чем тот, который вы могли бы получить с помощью любого отдельного метода — хотя результат, получаемый ансамблем, обычно ограничивается наилучшим методом оптимизации, содержащимся в нем.
Мы рассмотрим, как работают ансамбли оптимизации, как они могут выиграть от параллелизации, и разберем несколько примеров с использованием оптимизатора PSO, а также комбинаций PSO и Firefly. В заключение мы обсудим, как все это вписывается в науку о данных, а также некоторые полезные соображения относительно ансамблей оптимизации в целом.
Ансамбли оптимизации часто называются «гибридными системами» в научной литературе. Однако мы предпочитаем избегать добавления еще одного термина в обширный лексикон науки о данных, когда «ансамбль» хорошо работает как общий дескриптор, плюс это наиболее часто используемый термин в отрасли. Таким образом, если вы встретите термин «гибридный» в статье, как в случае варианта имитации отжига, упомянутого в главе 8, помните, что речь идет об ансамблевой системе.
Ансамбли оптимизации объединяют производительность различных систем оптимизации, решающих одну и ту же задачу. Эти системы могут быть итерациями одного и того же метода с различными параметрами и/или начальными значениями, или же они могут включать совершенно разные методы.
В качестве альтернативы, ансамбли оптимизации могут обмениваться данными между оптимизаторами, пытаясь еще больше улучшить точность результатов. Естественно, этот подход требует более глубокого понимания задействованных методов, а также более тонкой настройки каждого решения для конкретной задачи. В этой главе мы сосредоточимся на более простом ансамбле,
описано в предыдущем абзаце.
Роль параллелизации в ансамблях оптимизации
Параллелизация — это ключ к созданию ансамблей, поскольку она позволяет методам оптимизации работать одновременно. Подобно крупным системам моделирования данных, использующим различные машины (или компоненты, такие как GPU) для одновременной обработки данных при обучении системы, распараллеленные оптимизаторы могут обучаться и искать оптимальное решение одновременно, пробуя различные стратегии. Это может минимизировать риск застревания в локальном оптимуме или получения неточного решения из-за субоптимальной конфигурации параметров оптимизатора.
Таким образом, параллелизация лучше использует доступные ресурсы, экономя время и способствуя лучшим результатам. В зависимости от характера задачи, некоторые оптимизаторы могут быть разработаны для фокусирования только на одной части проблемы, такой как грубая оптимизация, происходящая в начале, прежде чем сосредоточиться на оптимальном решении. Это может потребовать некоторого продвинутого программирования, поэтому мы не будем углубляться в это в этой главе.
Фреймворк базового ансамбля оптимизации
Теперь давайте рассмотрим базовый ансамбль оптимизации, состоящий из двух оптимизаторов, работающих параллельно. Каждая система имеет свои параметры, но обе используют одну и ту же функцию приспособленности (иначе это не был бы ансамбль). После поиска решений они сравнивают свои результаты. Решение, соответствующее большему или меньшему значению (в зависимости от того, является ли задача максимизации или минимизации), выбирается как выход всей системы (см.
Рисунок 17).
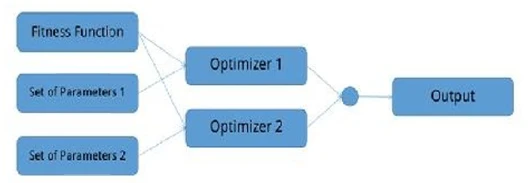
Рисунок 17. Диаграмма базового ансамбля оптимизации. Обратите внимание, что функция приспособленности одинакова для обоих оптимизаторов, и их выходы сравниваются перед получением единого результата. В этой диаграмме круговой узел означает слияние сигналов, полученных от двух оптимизаторов. Слияние происходит с использованием базового оператора типа min() или max(), в зависимости от используемого режима оптимизации.
Ключевая сила этой установки заключается в том, что два оптимизатора работают одновременно, поэтому вся система довольно быстрая. Вы можете создать ансамбль из более чем двух оптимизаторов, каждый со своим набором параметров, все они разделяют одну и ту же функцию приспособленности — при условии, что для их запуска достаточно вычислительных ресурсов.
Обратите внимание, что если используемые в ансамбле оптимизаторы имеют значительно разное время выполнения, это приведет к задержкам. Это связано с тем, что функция-обертка ансамбля должна ждать завершения работы всех исполнителей, не имея возможности опередить самого медленного оптимизатора.
Пример использования систем PSO в ансамбле
Чтобы сделать все это более наглядным, давайте рассмотрим базовый ансамбль оптимизации, состоящий из трех систем PSO, работающих на минимизацию заданной функции. Эти примеры основаны на четырехъядерном компьютере, поэтому они подходят для машины с такой вычислительной мощностью. Если вы используете более старый компьютер, вам нужно будет настроить количество работников в соответствии с его характеристиками — в противном случае вы можете испытывать задержки при
запуске кода ансамбля.
Для начала загрузим код PSO в память. Код для этого аналогичен описанному в Главе 6, поэтому не будем здесь его подробно рассматривать. Обратите внимание на одно небольшое улучшение, сделанное для повышения точности результатов: если наилучшее решение не улучшается за пределы заданного порога толерантности (tol) в течение буферного периода, максимальная скорость уменьшается на заданный коэффициент (в данном случае 0.618).
Далее нам необходимо загрузить пакет Distributed из базового пакета, чтобы мы могли использовать параллелизацию:
using Distributed
Далее необходимо добавить несколько рабочих процессов для применения параллелизации:
addprocs(3)
Мы можем убедиться, что у нас теперь 4 рабочих процесса (по одному для каждой системы PSO в ансамбле) следующим образом:
nprocs()
Несмотря на то, что для этого примера нам нужно всего 3 рабочих процесса, мы настоятельно рекомендуем добавить всех рабочих процессов, которые потребуются вам для всего проекта, на этапе инициализации. В противном случае вы рискуете серьезно запутаться в функциях, используемых этими рабочими процессами.
Затем нам необходимо загрузить функцию swi() для помощи с сортировкой матриц, доступную в пользовательском скрипте SortWithIndexes.jl:
include(“SortWithIndexes.jl”)
Затем нам необходимо определить функцию приспособленности (назовем ее FF) для оптимизаторов, и мы будем стремиться минимизировать ее:
@everywhere function FF(X::Array{Float64})
return y = X[1]^2 + abs(X[2]) +
sqrt(abs(X[3]*X[4])) + 1.0
end
Для того чтобы эта функция была доступна всем рабочим процессам, ей должен предшествовать метакоманда @everywhere. Тот же префикс добавляется к функции pso(), реализующей алгоритм PSO для каждого доступного рабочего процесса, а также к функции swi() для процесса сортировки матрицы. Если вы добавите дополнительных рабочих процессов позже, они не будут иметь доступа к функции FF — пока вы снова не запустите предыдущий код. Аналогично, если вы планируете запускать разные версии оптимизатора среди этих рабочих процессов, лучше активировать каждого рабочего процесса и запускать соответствующий код оптимизатора индивидуально, без метакоманды @everywhere.
Для функции-обертки, управляющей всем ансамблем, мы будем использовать следующий код. По сути, это мета-PSO функция, охватывающая все оптимизаторы ансамбля через их соответствующие рабочие процессы:
function ppso(ff::Function, minimize::Bool =
true, nv::Int64 = 4, ps::Int64 = 10*nv, ni::Int64
= 2000)
np = nprocs()
F = Any[ff for i = 1:np]
Z = pmap(pso, F)
G = Array{Float64}(undef, np)
for i = 1:np
G[i] = Z[i][2]
end
if minimize
ind = indmin(G)
else
ind = indmax(G)
end
println(G)
return Z[ind]
end
В данном случае нам не нужно использовать метакоманду @everywhere, поскольку функция не должна выполняться каждым отдельным рабочим процессом. Также команда println() не совсем необходима, хотя она может быть полезна, если вы хотите увидеть, как работают различные члены ансамбля.
Чтобы запустить ансамбль PSO на функции приспособленности F, просто наберите:
ppso(FF, true, 4)
Решение этого ансамбля очень близко к глобальному оптимуму [0, 0, 0, R] и [0, 0, R, 0] (где R — любое действительное число), имеющее значение приспособленности 1.0. Найденное в данном случае решение [-0.00527571, -1.66536e-6, 1.44652e-5, -3.29118e-6] соответствует значению приспособленности около 1.00008. Это довольно близко к фактическому оптимальному значению, хотя весь процесс нахождения этого решения был не заметно медленнее, чем запуск одного поиска PSO.
Из-за настроек по умолчанию функции ppso(), даже если мы набрали ppso(FF), ансамбль все равно будет работать. Также помните, что для использования этой функции для задачи максимизации, вам необходимо сначала установить второй параметр в «false»:
ppso(FF, false, 4)
Пример использования ансамбля PSO и Firefly
Теперь рассмотрим еще один базовый ансамбль оптимизации, на этот раз включающий два разных оптимизатора: оптимизатор PSO и оптимизатор Firefly. (Для ознакомления с этим методом оптимизации см. соответствующий абзац Главы 6). Цель в данном случае — снова минимизировать заданную функцию. Чтобы сделать вещи интереснее, у нас будет по два оптимизатора для каждого алгоритма, в общей сложности 4 работника.
В этом примере нам понадобится код как для PSO, так и для Firefly. Для последнего нам необходимо использовать некоторые вспомогательные функции, все из которых содержатся в соответствующем ноутбуке. Для краткости мы опустим этот код здесь. Система оптимизации Firefly реализована с использованием функции ffo().
Для ансамбля мы можем использовать функцию-обертку co(), которая означает «объединенный оптимизатор»:
function co(ff::Function, minimize::Bool = true, nv::Int64 = 5) np = round(Int64, nprocs() / 2) # number of processors for each optimizer N = 2*np
F = Function[ff for i = 1:np]
M = Bool[minimize for i = 1:np]
NV = Int64[nv for i = 1:np]
G = Array{Float64}(undef, N)
X = pmap((ff, minimize, nv) -> ffo(ff,
minimize, nv), F, M, NV)
Y = pmap((ff, minimize, nv) -> pso(ff,
minimize, nv), F, M, NV)
Z = vcat(X, Y)
for i = 1:N
G[i] = Z[i][2]
end
if minimize
ind = findmin(G)[2]
else
ind = findmax(G)[2]
end
println(G)
return Z[ind]
end
Как и в предыдущем примере, нам не нужно использовать метакоманду @everywhere для этой функции, так как она не должна выполняться каждым отдельным рабочим процессом. Помните, что нам нужна метакоманда @everywhere только если код должен выполняться каждым отдельным рабочим процессом, т.е. параллельно. Функции-обертки, как правило, в этом не нуждаются.
Команда println() в функции предназначена исключительно для образовательных целей, позволяя просматривать результаты работы различных членов ансамбля. В данном случае это особенно интересно, так как у нас есть оптимизаторы из двух разных семейств (первые два — PSO, последние два — Firefly).
Чтобы протестировать все это на функции приспособленности F (определенной ранее), нам просто нужно набрать:
co(F, true, 4)
Это возвращает решение, очень близкое к глобальному оптимуму, [-0.0103449, 6.77669e-8, -7.33842e-7, -7.93017e-10], соответствующее значению приспособленности около 1.0001. Значения приспособленности лучших решений оптимизаторов равны: 1.01052, 1.00636, 1.0003 и 1.00011, соответственно. Хотя конечный результат не так точен, как в предыдущем примере, он в целом довольно хорош. Учитывая, что системы PSO не так хорошо справились с этой задачей, ансамблю удалось хорошо себя проявить благодаря двум другим оптимизаторам Firefly.
Функция co() универсальна по своей сути, с точки зрения количества используемых работников. Она по сути распределяет половину доступных работников одному оптимизатору, а остальных — другому. Вы можете экспериментировать с различными числами работников, особенно если у вас достаточно вычислительных мощностей.
Как ансамбли оптимизации вписываются в конвейер науки о данных
На этом этапе вы, возможно, задаетесь вопросом, насколько все это ансамблевое оптимизационное дело актуально для процесса науки о данных. В конце концов, вы можете получать знания с помощью более традиционных методов, таких как базовые системы машинного обучения и статистические модели, или с помощью систем глубокого обучения, которые мы рассмотрели в первой части книги. Как ансамбли оптимизации улучшают эти существующие методологии?
Короче говоря, большинство современных задач науки о данных в той или иной степени связаны с оптимизацией, и традиционные оптимизаторы просто не справятся. Более старые методы хорошо работали для простых задач, для которых они были созданы. Всего несколько десятилетий назад аналитики (с большим терпением и талантом к математике) решали простые задачи вручную. Но наука о данных — огромная область с огромным количеством сложных данных, включающая множество измерений и переменных.
Более того, хотя оптимизаторы, которые мы изучали, могут справляться с этими проблемами, зачастую у нас нет времени на их тонкую настройку. Именно здесь на помощь приходят ансамбли оптимизации. От выполнения выбора признаков до оптимизации границ параметров в одноклассовой SVM для обнаружения аномалий, оптимизация необходима для многих проектов в области науки о данных.
Что более важно, эффективное решение сложных задач оптимизации
с помощью ансамблей даст вам лучшую перспективу на решение проблем в науке о данных. Многие доступные методы уже оптимизированы, но иногда вам может потребоваться новаторский подход, решение задачи, которая раньше не решалась (по крайней мере, в мире открытого исходного кода). Именно здесь опыт работы с ансамблями (и другими темами, выходящими за рамки базового уровня) может пригодиться, поскольку не все задачи можно или нужно решать готовыми методами. Сфера деятельности хорошего специалиста по данным больше не ограничивается традиционными методами науки о данных, быстро расширяясь, включая методы ИИ, такие как ансамбли оптимизации.
Советы по ансамблям
Ансамбли оптимизации, рассмотренные в этой главе, могут показаться прямолинейными, но, как обычно, следует помнить о нескольких ключевых моментах. Например, необходимо убедиться, что оптимизаторы правильно настроены, установив соответствующие параметры со значениями, которые имеют смысл для рассматриваемой задачи. В противном случае результаты могут быть не столь полезными, или будут потрачены значительные вычислительные ресурсы (например, из-за задержки сходимости).
Кроме того, лучше использовать те оптимизаторы, с которыми вы знакомы и хорошо их понимаете. Таким образом, вы сможете получить хорошие результаты от такой системы, даже если используемые вами оптимизаторы являются экземплярами одного и того же алгоритма. Кроме того, из-за их стохастической природы они неизбежно будут давать разные решения при каждом запуске, поэтому их включение в ансамбль определенно может оказать положительное влияние на результат оптимизации.
При построении ансамбля оптимизации обращайте внимание на имеющиеся в вашем распоряжении вычислительные мощности. Julia может создавать столько рабочих процессов, сколько запрошено, но если мощность рабочих процессов превышает производительность потоков обработки, доступных на вашей машине, ансамбль не будет эффективным. Некоторым потокам придется выполнять больше задач, чем другим, что приведет к дисбалансу рабочей нагрузки, что неизбежно задержит всю систему. Помните, что рабочие процессы могут соответствовать отдельным CPU или GPU, когда их количество невелико. Однако, если их количество превышает общее количество потоков обработки, доступных Julia, то возникнет проблема, даже если она не вызовет ошибок или исключений.
Более того, использование ансамбля оптимизации не гарантирует, что решение будет глобальным оптимумом. Иногда даже группа ансамблей может застрять в локальном оптимуме, давая субоптимальное решение в конце конвейера. Тем не менее, шансы на это меньше при использовании ансамбля, чем при использовании одиночного оптимизатора.
Резюме
- Ансамбли оптимизации (также называемые «гибридными системами») используют комбинацию оптимизаторов для решения заданной функции приспособленности. Такой ансамбль может дать результат по крайней мере не хуже, чем результат его наилучшего члена.
- Ансамбли оптимизации бывают разных форм. Простые ансамбли запускают два (или более) оптимизатора параллельно на одной задаче, а затем сравнивают их выходы. Оптимизаторами могут быть алгоритмы из разных семейств, хотя лучше использовать алгоритмы с похожим временем выполнения для обеспечения эффективности.
- Кодирование в базовом ансамбле оптимизации довольно простое. Используйте метакоманду @everywhere, чтобы гарантировать доступность всех функций оптимизатора всем рабочим процессам в ансамбле.
- Понимание внутренних механизмов ансамблей оптимизации поможет вам отточить свои навыки решения проблем и позволит решать сложные и комплексные задачи науки о данных. Такие проблемы могут быть не обычными, но когда они возникают, они часто являются критически важными для рассматриваемого проекта.
- При работе с ансамблями оптимизации не забывайте правильно устанавливать параметры и обращать внимание на доступные вычислительные мощности.
- Результат ансамбля оптимизации не гарантированно является глобальным оптимумом, но почти наверняка лучше, чем результат любого из его компонентов по отдельности.