Глава 1. Введение
1.1 Что такое машинное обучение
Машинное обучение — это подраздел компьютерных наук, занимающийся созданием алгоритмов, которые для своей полезной работы опираются на набор примеров некоторого явления. Эти примеры могут быть взяты из природы, созданы вручную людьми или сгенерированы другим алгоритмом.
Машинное обучение также можно определить как процесс решения практической задачи путем 1) сбора набора данных и 2) алгоритмического построения статистической модели на основе этого набора данных. Предполагается, что эта статистическая модель будет каким-то образом использоваться для решения практической задачи.
Для краткости я использую термины «обучение» и «машинное обучение» взаимозаменяемо.
1.2 Типы обучения
Обучение может быть с учителем, полу управляемым, без учителя и с подкреплением.
1.2.1 Обучение с учителем
При обучении с учителем1 набор данных представляет собой коллекцию размеченных примеров \({(x_i, y_i)}_{i=1}^N\). Каждый элемент \(x_i\) среди \(N\) называется вектором признаков. Вектор признаков — это вектор, в котором каждое измерение \(j = 1, \dots, D\) содержит значение, которое каким-то образом описывает пример. Это значение называется признаком и обозначается как \(x^{(j)}\). Например, если каждый пример \(x\) в нашей коллекции представляет человека, то первый признак, \(x^{(1)}\), может содержать рост в см, второй признак, \(x^{(2)}\), может содержать вес в кг, \(x^{(3)}\) — пол, и так далее. Для всех примеров в наборе данных признак на позиции \(j\) в векторе признаков всегда содержит один и тот же тип информации. Это означает, что если \(x^{(2)}_i\) содержит вес в кг в некотором примере \(x_i\), то \(x^{(2)}_k\) также будет содержать вес в кг в каждом примере \(x_k\), \(k = 1, \dots, N\). Метка \(y_i\) может быть либо элементом, принадлежащим конечному набору классов \({1, 2, \dots, C}\), либо вещественным числом2, либо более сложной структурой, такой как вектор, матрица, дерево или граф. Если не указано иное, в этой книге \(y_i\) является либо одним из конечного набора классов, либо вещественным числом. Класс можно рассматривать как категорию, к которой принадлежит пример. Например, если ваши примеры — это сообщения электронной почты, а ваша проблема — обнаружение спама, то у вас есть два класса \({спам, неспам}\).
Цель алгоритма обучения с учителем — использовать набор данных для создания модели, которая принимает на вход вектор признаков \(x\) и выводит информацию, позволяющую определить метку для этого вектора признаков. Например, модель, созданная с использованием набора данных о людях, может принимать на вход вектор признаков, описывающий человека, и выводить вероятность того, что у этого человека рак.
1Если термин выделен жирным шрифтом, это означает, что его можно найти в указателе в конце книги.
2Вещественное число — это величина, которая может представлять расстояние вдоль линии. Примеры: 0, -256.34, 1000, 1000.2.
1.2.2 Обучение без учителя
При обучении без учителя набор данных представляет собой коллекцию неразмеченных примеров \({x_i}_{i=1}^N\). Опять же, \(x\) — это вектор признаков, и цель алгоритма обучения без учителя — создать модель, которая принимает на вход вектор признаков \(x\) и либо преобразует его в другой вектор, либо в значение, которое можно использовать для решения практической задачи. Например, при кластеризации модель возвращает идентификатор кластера для каждого вектора признаков в наборе данных. При снижении размерности выходными данными модели является вектор признаков, имеющий меньше признаков, чем входной \(x\); при обнаружении выбросов выходными данными является вещественное число, указывающее, насколько \(x\) отличается от «типичного» примера в наборе данных.
1.2.3 Полуавтоматическое обучение
При полуавтоматическом обучении набор данных содержит как размеченные, так и неразмеченные примеры. Обычно количество неразмеченных примеров намного превышает количество размеченных примеров. Цель алгоритма полуавтоматического обучения такая же, как и цель алгоритма обучения с учителем. Надежда здесь заключается в том, что использование большого количества неразмеченных примеров может помочь алгоритму обучения найти (мы можем сказать «произвести» или «вычислить») лучшую модель.
Может показаться нелогичным, что обучение может выиграть от добавления большего количества неразмеченных примеров. Кажется, что мы добавляем больше неопределенности в проблему. Однако, когда вы добавляете неразмеченные примеры, вы добавляете больше информации о вашей проблеме: больший объем выборки лучше отражает распределение вероятностей, из которого были взяты данные, которые мы разметили. Теоретически, алгоритм обучения должен быть в состоянии использовать эту дополнительную информацию.
1.2.4 Обучение с подкреплением
Обучение с подкреплением — это подраздел машинного обучения, в котором машина «живет» в среде и способна воспринимать состояние этой среды как вектор признаков. Машина может выполнять действия в каждом состоянии. Различные действия приносят разные награды и также могут перемещать машину в другое состояние среды. Цель алгоритма обучения с подкреплением — изучить политику.
Политика — это функция (аналогичная модели в обучении с учителем), которая принимает на вход вектор признаков состояния и выводит оптимальное действие для выполнения в этом состоянии. Действие является оптимальным, если оно максимизирует ожидаемую среднюю награду.
Обучение с подкреплением решает особый тип задач, где принятие решений является последовательным, а цель — долгосрочной, например, игра, робототехника, управление ресурсами или логистика. В этой книге я делаю акцент на принятии одномоментных решений, где входные примеры независимы друг от друга, а прогнозы, сделанные в прошлом, не влияют на будущие. Я оставляю обучение с подкреплением за рамками этой книги.
1.3 Как работает обучение с учителем
В этом разделе я кратко объясню, как работает обучение с учителем, чтобы у вас была общая картина всего процесса, прежде чем мы углубимся в детали. Я решил использовать обучение с учителем в качестве примера, потому что это тип машинного обучения, наиболее часто используемый на практике.
Процесс обучения с учителем начинается со сбора данных. Данные для обучения с учителем — это коллекция пар (вход, выход). Вход может быть чем угодно, например, сообщениями электронной почты, изображениями или данными с датчиков. Выходные данные обычно представляют собой вещественные числа или метки (например, «спам», «не спам», «кошка», «собака», «мышь» и т.д.). В некоторых случаях выходные данные представляют собой векторы (например, четыре координаты прямоугольника вокруг человека на изображении), последовательности (например, [«прилагательное», «прилагательное», «существительное»] для входа «большая красивая машина») или имеют какую-то другую структуру.
Допустим, проблема, которую вы хотите решить с помощью обучения с учителем, — это обнаружение спама. Вы собираете данные, например, 10 000 сообщений электронной почты, каждое с меткой «спам» или «не спам» (вы можете добавить эти метки вручную или заплатить кому-то за это). Теперь вам нужно преобразовать каждое сообщение электронной почты в вектор признаков.
Аналитик данных решает, основываясь на своем опыте, как преобразовать сущность реального мира, такую как сообщение электронной почты, в вектор признаков. Один из распространенных способов преобразования текста в вектор признаков, называемый мешком слов, заключается в том, чтобы взять словарь английских слов (допустим, он содержит 20 000 слов, отсортированных по алфавиту) и определить, что в нашем векторе признаков:
- первый признак равен 1, если сообщение содержит слово «a»; в противном случае этот признак равен 0;
- второй признак равен 1, если сообщение содержит слово «aaron»; в противном случае этот признак равен 0;
- ...
- признак на позиции 20 000 равен 1, если сообщение содержит слово «zulu»; в противном случае этот признак равен 0.
Вы повторяете вышеуказанную процедуру для каждого сообщения электронной почты в нашей коллекции, что дает нам 10 000 векторов признаков (каждый вектор имеет размерность 20 000) и метку («спам»/«не спам»).
Теперь у вас есть машиночитаемые входные данные, но выходные метки все еще находятся в форме удобочитаемого текста. Некоторые алгоритмы обучения требуют преобразования меток в числа. Например, некоторые алгоритмы требуют чисел, таких как 0 (для представления метки «не спам») и 1 (для представления метки «спам»). Алгоритм, который я использую для иллюстрации обучения с учителем, называется Метод опорных векторов (SVM). Этот алгоритм требует, чтобы положительная метка (в нашем случае это «спам») имела числовое значение +1 (один), а отрицательная метка («не спам») имела значение -1 (минус один).
На данный момент у вас есть набор данных и алгоритм обучения, так что вы готовы применить алгоритм обучения к набору данных, чтобы получить модель.
SVM рассматривает каждый вектор признаков как точку в многомерном пространстве (в нашем случае пространство 20 000-мерное). Алгоритм размещает все векторы признаков на воображаемом 20 000-мерном графике и проводит воображаемую 19 999-мерную линию (гиперплоскость), которая разделяет примеры с положительными метками от примеров с отрицательными метками. В машинном обучении граница, разделяющая примеры разных классов, называется границей принятия решений.
Уравнение гиперплоскости задается двумя параметрами: вещественным вектором \(w\) той же размерности, что и наш входной вектор признаков \(x\), и вещественным числом \(b\), вот так:
\[ wx - b = 0, \]где выражение \(wx\) означает \(w^{(1)}x^{(1)} + w^{(2)}x^{(2)} + \dots + w^{(D)}x^{(D)}\), а \(D\) — количество измерений вектора признаков \(x\).
(Если некоторые уравнения вам сейчас непонятны, в Главе 2 мы вернемся к математическим и статистическим концепциям, необходимым для их понимания. На данный момент постарайтесь уловить интуицию происходящего. Все станет яснее после прочтения следующей главы.)
Теперь предсказанная метка для некоторого входного вектора признаков \(x\) дается следующим образом:
\[ y = \text{sign}(wx - b), \]где \(\text{sign}\) — это математический оператор, который принимает любое значение на вход и возвращает +1, если вход — положительное число, или -1, если вход — отрицательное число.
Цель алгоритма обучения — в данном случае SVM — использовать набор данных и найти оптимальные значения \(w^*\) и \(b^*\) для параметров \(w\) и \(b\). Как только алгоритм обучения определит эти оптимальные значения, модель \(f(x)\) определяется как:
\[ f(x) = \text{sign}(w^*x - b^*) \]Следовательно, чтобы предсказать, является ли сообщение электронной почты спамом или нет, используя модель SVM, вы должны взять текст сообщения, преобразовать его в вектор признаков, затем умножить этот вектор на \(w^*\), вычесть \(b^*\) и взять знак результата. Это даст нам предсказание (+1 означает «спам», -1 означает «не спам»).
Теперь, как машина находит \(w^*\) и \(b^*\)? Она решает задачу оптимизации. Машины хорошо справляются с оптимизацией функций при наличии ограничений.
Так каковы же ограничения, которые мы хотим удовлетворить здесь? Прежде всего, мы хотим, чтобы модель правильно предсказывала метки наших 10 000 примеров. Помните, что каждый пример \(i = 1, \dots, 10000\) задан парой \((x_i, y_i)\), где \(x_i\) — это вектор признаков примера \(i\), а \(y_i\) — его метка, которая принимает значения либо -1, либо +1. Таким образом, ограничения естественны:
\begin{align*} wx_i - b \ge +1 & \quad \text{если } y_i = +1, \\ wx_i - b \le -1 & \quad \text{если } y_i = -1. \end{align*}Мы также предпочли бы, чтобы гиперплоскость разделяла положительные примеры от отрицательных с наибольшим зазором (margin). Зазор — это расстояние между ближайшими примерами двух классов, определяемое границей принятия решений. Большой зазор способствует лучшей обобщающей способности (generalization), то есть тому, насколько хорошо модель будет классифицировать новые примеры в будущем. Чтобы достичь этого, нам нужно минимизировать евклидову норму вектора \(w\), обозначаемую как \(\|w\|\) и задаваемую \(\sqrt{\sum_{j=1}^D (w^{(j)})^2}\).
Таким образом, задача оптимизации, которую мы хотим, чтобы машина решила, выглядит так:
Минимизировать \(\|w\|\) при условии \(y_i(wx_i - b) \ge 1\) для \(i = 1, \dots, N\). Выражение \(y_i(wx_i - b) \ge 1\) — это просто компактный способ записи двух вышеуказанных ограничений.
Решение этой задачи оптимизации, задаваемое \(w^*\) и \(b^*\), называется статистической моделью, или просто моделью. Процесс построения модели называется обучением (training).
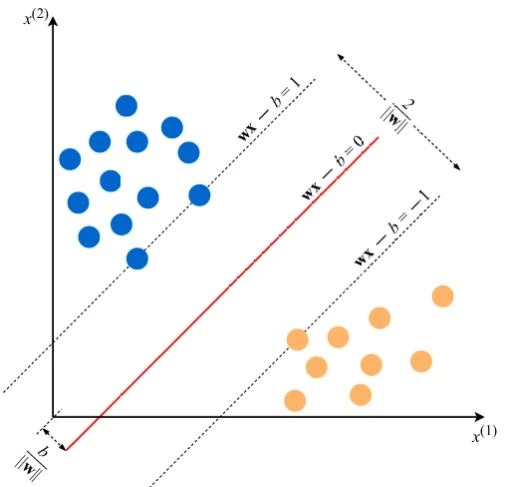
Для двумерных векторов признаков проблема и решение могут быть визуализированы, как показано на Рисунке 1 (в файле pdf). Синие и оранжевые круги представляют соответственно положительные и отрицательные примеры, а линия, заданная уравнением \(wx - b = 0\), является границей принятия решений.
Почему, минимизируя норму \(w\), мы находим наибольший зазор между двумя классами? Геометрически уравнения \(wx - b = 1\) и \(wx - b = -1\) определяют две параллельные гиперплоскости, как вы видите на Рисунке 1 (в файле pdf). Расстояние между этими гиперплоскостями равно \(\frac{2}{\|w\|}\), поэтому чем меньше норма \(\|w\|\), тем больше расстояние между этими двумя гиперплоскостями.
Вот как работает метод опорных векторов. Эта конкретная версия алгоритма строит так называемую линейную модель. Она называется линейной, потому что граница принятия решений является прямой линией (или плоскостью, или гиперплоскостью). SVM также может включать ядра (kernels), которые могут сделать границу принятия решений произвольно нелинейной. В некоторых случаях может быть невозможно идеально разделить две группы точек из-за шума в данных, ошибок разметки или выбросов (примеров, сильно отличающихся от «типичного» примера в наборе данных). Другая версия SVM также может включать гиперпараметр3 штрафа за неправильную классификацию обучающих примеров определенных классов. Мы более подробно изучим алгоритм SVM в Главе 3.
На данный момент вы должны запомнить следующее: любой алгоритм обучения классификации, который строит модель, неявно или явно создает границу принятия решений. Граница принятия решений может быть прямой, изогнутой, иметь сложную форму или быть суперпозицией некоторых геометрических фигур. Форма границы принятия решений определяет точность (accuracy) модели (то есть долю примеров, метки которых предсказаны правильно). Форма границы принятия решений, способ ее алгоритмического или математического вычисления на основе обучающих данных отличают один алгоритм обучения от другого.
На практике следует учитывать еще два существенных отличия алгоритмов обучения: скорость построения модели и время обработки предсказания. Во многих практических случаях вы предпочтете алгоритм обучения, который строит менее точную модель, но быстро. Кроме того, вы можете предпочесть менее точную модель, которая намного быстрее делает предсказания.
1.4 Почему модель работает на новых данных
Почему модель, обученная машиной, способна правильно предсказывать метки новых, ранее невиданных примеров? Чтобы понять это, посмотрите на график на Рисунке 1 (в файле pdf). Если два класса отделимы друг от друга границей принятия решений, то, очевидно, примеры, принадлежащие каждому классу, расположены в двух разных подпространствах, которые создает граница принятия решений.
Если примеры, использованные для обучения, были выбраны случайным образом, независимо друг от друга и по одной и той же процедуре, то статистически более вероятно, что новый отрицательный пример будет расположен на графике где-то не слишком далеко от других отрицательных примеров. То же самое касается нового положительного примера: он, вероятно, появится в окрестности других положительных примеров. В таком случае наша граница принятия решений все равно будет, с высокой вероятностью, хорошо разделять новые положительные и отрицательные примеры. В других, менее вероятных ситуациях, наша модель будет делать ошибки, но поскольку такие ситуации менее вероятны, количество ошибок, скорее всего, будет меньше, чем количество правильных предсказаний.
Интуитивно, чем больше набор обучающих примеров, тем менее вероятно, что новые примеры будут отличаться (и лежать на графике далеко) от примеров, использованных для обучения.
Чтобы минимизировать вероятность ошибок на новых примерах, алгоритм SVM, ища наибольший зазор, явно пытается провести границу принятия решений таким образом, чтобы она лежала как можно дальше от примеров обоих классов.
Читателю, заинтересованному в том, чтобы узнать больше об обучаемости (learnability) и понять тесную взаимосвязь между ошибкой модели, размером обучающего набора, формой математического уравнения, определяющего модель, и временем, необходимым для построения модели, рекомендуется прочитать о PAC-обучении. Теория PAC (от «Probably Approximately Correct» — вероятно, приблизительно правильный) помогает анализировать, будет ли и при каких условиях алгоритм обучения вероятно выдавать приблизительно правильный классификатор.
1.5 Предупреждение о подделках
По состоянию на апрель 2019 года Интернет полон поддельных копий моей книги, включая печатные копии. Чтобы избежать покупки подделки, я рекомендую переходить по ссылкам на вспомогательном веб-сайте книги themlbook.com. Даже если вы покупаете на Amazon, убедитесь, что вы покупаете непосредственно у Amazon, а не у стороннего продавца.
3Гиперпараметр — это свойство алгоритма обучения, обычно (но не всегда) имеющее числовое значение. Это значение влияет на то, как работает алгоритм. Эти значения не изучаются алгоритмом самостоятельно из данных. Они должны быть установлены аналитиком данных перед запуском алгоритма.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения