Глава 2. Обозначения и определения
2.1 Обозначения
Давайте начнем с повторения математических обозначений, которые мы все изучали в школе, но некоторые, вероятно, забыли сразу после выпускного.
2.1.1 Структуры данных
Скаляр — это простое числовое значение, например 15 или -3.25. Переменные или константы, принимающие скалярные значения, обозначаются курсивной буквой, например, x или a.
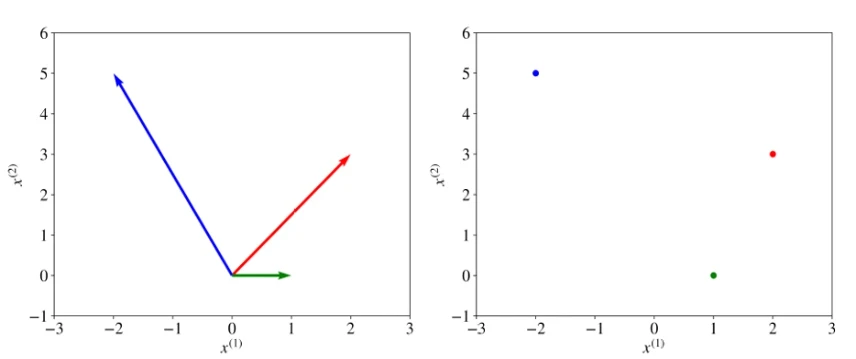
Вектор — это упорядоченный список скалярных значений, называемых атрибутами. Мы обозначаем вектор жирным символом, например, x или w. Векторы можно визуализировать как стрелки, указывающие в некоторых направлениях, а также как точки в многомерном пространстве. Иллюстрации трех двумерных векторов, a = [2, 3], b = [-2, 5] и c = [1, 0], приведены на Рисунке 1 (в pdf). Мы обозначаем атрибут вектора курсивным значением с индексом, например: w(j) или x(j). Индекс j обозначает конкретное измерение вектора, позицию атрибута в списке. Например, в векторе a, показанном красным на Рисунке 1, a(1) = 2 и a(2) = 3.
Обозначение x(j) не следует путать с оператором возведения в степень, таким как 2 в x2 (в квадрате) или 3 в x3 (в кубе). Если мы хотим применить оператор возведения в степень, скажем, квадрат, к индексированному атрибуту вектора, мы пишем так: (x(j))2.
Переменная может иметь два или более индексов, например: x(j)i или x(k)i,j. Например, в нейронных сетях мы обозначаем как x(j)l,u входной признак j блока u в слое l.
Матрица — это прямоугольный массив чисел, расположенных по строкам и столбцам. Ниже приведен пример матрицы с двумя строками и тремя столбцами,
\[ \begin{pmatrix} 2 & 4 & -3 \\ 21 & -6 & -1 \end{pmatrix}. \]Матрицы обозначаются жирными заглавными буквами, такими как A или W.
Множество — это неупорядоченная коллекция уникальных элементов. Мы обозначаем множество каллиграфической заглавной буквой, например, \(\mathcal{S}\). Множество чисел может быть конечным (включать фиксированное количество значений). В этом случае оно обозначается с помощью фигурных скобок, например, {1, 3, 18, 23, 235} или {x1, x2, x3, x4, ..., xn}. Множество может быть бесконечным и включать все значения в некотором интервале. Если множество включает все значения между a и b, включая a и b, оно обозначается с помощью квадратных скобок как [a, b]. Если множество не включает значения a и b, такое множество обозначается с помощью круглых скобок: (a, b). Например, множество [0, 1] включает такие значения, как 0, 0.0001, 0.25, 0.784, 0.9995 и 1.0. Специальное множество, обозначаемое \(\mathbb{R}\), включает все числа от минус бесконечности до плюс бесконечности.
Когда элемент x принадлежит множеству \(\mathcal{S}\), мы пишем \(x \in \mathcal{S}\). Мы можем получить новое множество \(\mathcal{S}_3\) как пересечение двух множеств \(\mathcal{S}_1\) и \(\mathcal{S}_2\). В этом случае мы пишем \(\mathcal{S}_3 \leftarrow \mathcal{S}_1 \cap \mathcal{S}_2\). Например, {1, 3, 5, 8} ∩ {1, 8, 4} дает новое множество {1, 8}.
Мы можем получить новое множество \(\mathcal{S}_3\) как объединение двух множеств \(\mathcal{S}_1\) и \(\mathcal{S}_2\). В этом случае мы пишем \(\mathcal{S}_3 \leftarrow \mathcal{S}_1 \cup \mathcal{S}_2\). Например, {1, 3, 5, 8} ∪ {1, 8, 4} дает новое множество {1, 3, 4, 5, 8}.
2.1.2 Обозначение заглавной сигмы
Суммирование по коллекции \(\mathcal{X} = \{x_1, x_2, \dots, x_{n-1}, x_n\}\) или по атрибутам вектора x = [x(1), x(2), ..., x(m-1), x(m)] обозначается следующим образом:
\[ \sum_{i=1}^n x_i \stackrel{\text{def}}{=} x_1 + x_2 + \dots + x_{n-1} + x_n, \quad \text{или же:} \quad \sum_{j=1}^m x^{(j)} \stackrel{\text{def}}{=} x^{(1)} + x^{(2)} + \dots + x^{(m-1)} + x^{(m)}. \]Обозначение \(\stackrel{\text{def}}{=}\) означает «определяется как».
2.1.3 Обозначение заглавной Пи
Обозначение, аналогичное заглавной сигме, — это обозначение заглавной Пи. Оно обозначает произведение элементов в коллекции или атрибутов вектора:
\[ \prod_{i=1}^n x_i \stackrel{\text{def}}{=} x_1 \cdot x_2 \cdot \dots \cdot x_{n-1} \cdot x_n, \]где \(a \cdot b\) означает a, умноженное на b. По возможности мы опускаем \(\cdot\) для упрощения обозначения, так что ab также означает a, умноженное на b.
2.1.4 Операции над множествами
Оператор создания производного множества выглядит так: \(\mathcal{S}' \leftarrow \{x^2 | x \in \mathcal{S}, x > 3\}\). Это обозначение означает, что мы создаем новое множество \(\mathcal{S}'\), помещая в него x в квадрате таким образом, что x находится в \(\mathcal{S}\), и x больше 3.
Оператор мощности \(|\mathcal{S}|\) возвращает количество элементов в множестве \(\mathcal{S}\).
2.1.5 Операции над векторами
Сумма двух векторов x + z определяется как вектор [x(1) + z(1), x(2) + z(2), ..., x(m) + z(m)].
Разность двух векторов x - z определяется как [x(1) - z(1), x(2) - z(2), ..., x(m) - z(m)].
Вектор, умноженный на скаляр, является вектором. Например, \(x \cdot c \stackrel{\text{def}}{=} [cx^{(1)}, cx^{(2)}, \dots, cx^{(m)}]\).
Скалярное произведение двух векторов является скаляром. Например, \(wx \stackrel{\text{def}}{=} \sum_{i=1}^m w^{(i)}x^{(i)}\). В некоторых книгах скалярное произведение обозначается как w · x. Два вектора должны иметь одинаковую размерность. В противном случае скалярное произведение не определено.
Умножение матрицы W на вектор x приводит к другому вектору. Пусть наша матрица будет,
\[ \mathbf{W} = \begin{pmatrix} w^{(1,1)} & w^{(1,2)} & w^{(1,3)} \\ w^{(2,1)} & w^{(2,2)} & w^{(2,3)} \end{pmatrix}. \]Когда векторы участвуют в операциях с матрицами, вектор по умолчанию представляется как матрица с одним столбцом. Когда вектор находится справа от матрицы, он остается вектором-столбцом. Мы можем умножить матрицу на вектор только в том случае, если вектор имеет столько же строк, сколько столбцов в матрице. Пусть наш вектор будет \(\mathbf{x} \stackrel{\text{def}}{=} [x^{(1)}, x^{(2)}, x^{(3)}]\). Тогда \(\mathbf{Wx}\) — это двумерный вектор, определяемый как,
\[ \mathbf{Wx} = \begin{pmatrix} w^{(1,1)} & w^{(1,2)} & w^{(1,3)} \\ w^{(2,1)} & w^{(2,2)} & w^{(2,3)} \end{pmatrix} \begin{bmatrix} x^{(1)} \\ x^{(2)} \\ x^{(3)} \end{bmatrix} \stackrel{\text{def}}{=} \begin{pmatrix} w^{(1,1)}x^{(1)} + w^{(1,2)}x^{(2)} + w^{(1,3)}x^{(3)} \\ w^{(2,1)}x^{(1)} + w^{(2,2)}x^{(2)} + w^{(2,3)}x^{(3)} \end{pmatrix} = \begin{pmatrix} \mathbf{w}^{(1)}\mathbf{x} \\ \mathbf{w}^{(2)}\mathbf{x} \end{pmatrix} \]Если бы наша матрица имела, скажем, пять строк, результатом произведения был бы пятимерный вектор.
Когда вектор находится слева от матрицы при умножении, он должен быть транспонирован перед умножением на матрицу. Транспонирование вектора x, обозначаемое как xT, превращает вектор-столбец в вектор-строку. Допустим,
\[ \mathbf{x} = \begin{pmatrix} x^{(1)} \\ x^{(2)} \end{pmatrix}, \quad \text{тогда} \quad \mathbf{x}^\top \stackrel{\text{def}}{=} \begin{pmatrix} x^{(1)} & x^{(2)} \end{pmatrix}. \]Умножение вектора x на матрицу W задается как \(\mathbf{x}^\top \mathbf{W}\),
\[ \mathbf{x}^\top \mathbf{W} = \begin{pmatrix} x^{(1)} & x^{(2)} \end{pmatrix} \begin{pmatrix} w^{(1,1)} & w^{(1,2)} & w^{(1,3)} \\ w^{(2,1)} & w^{(2,2)} & w^{(2,3)} \end{pmatrix} \stackrel{\text{def}}{=} \begin{pmatrix} w^{(1,1)}x^{(1)} + w^{(2,1)}x^{(2)}, & w^{(1,2)}x^{(1)} + w^{(2,2)}x^{(2)}, & w^{(1,3)}x^{(1)} + w^{(2,3)}x^{(2)} \end{pmatrix} \]Как вы можете видеть, мы можем умножить вектор на матрицу только в том случае, если вектор имеет ту же размерность, что и количество строк в матрице.
2.1.6 Функции
Функция — это отношение, которое связывает каждый элемент x множества \(\mathcal{X}\), области определения функции, с единственным элементом y другого множества \(\mathcal{Y}\), области значений функции. У функции обычно есть имя. Если функция называется f, это отношение обозначается как \(y = f(x)\) (читается «эф от икс»), элемент x является аргументом или входом функции, а y — значением функции или выходом. Символ, используемый для представления входа, является переменной функции (мы часто говорим, что f — это функция от переменной x).
Мы говорим, что \(f(x)\) имеет локальный минимум в точке \(x = c\), если \(f(x) \ge f(c)\) для любого x в некотором открытом интервале вокруг \(x = c\). Интервал — это множество вещественных чисел со свойством, что любое число, лежащее между двумя числами в множестве, также включено в множество. Открытый интервал не включает свои конечные точки и обозначается с помощью круглых скобок. Например, (0, 1) означает «все числа больше 0 и меньше 1». Минимальное значение среди всех локальных минимумов называется глобальным минимумом. См. иллюстрацию на Рисунке 2 (в pdf).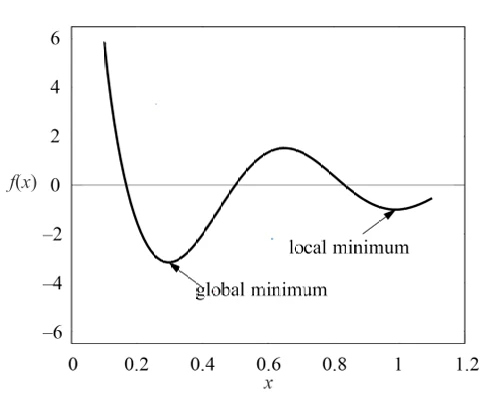
Векторная функция, обозначаемая как \(\mathbf{y} = \mathbf{f}(\mathbf{x})\), — это функция, которая возвращает вектор y. Она может иметь векторный или скалярный аргумент.
2.1.7 Max и Arg Max
Для множества значений \(\mathcal{A} = \{a_1, a_2, \dots, a_n\}\) оператор \(\max_{a \in \mathcal{A}} f(a)\) возвращает наибольшее значение \(f(a)\) для всех элементов в множестве \(\mathcal{A}\). С другой стороны, оператор \(\arg \max_{a \in \mathcal{A}} f(a)\) возвращает элемент множества \(\mathcal{A}\), который максимизирует \(f(a)\).
Иногда, когда множество подразумевается или бесконечно, мы можем писать \(\max_a f(a)\) или \(\arg \max_a f(a)\).
Операторы min и arg min действуют аналогичным образом.
2.1.8 Оператор присваивания
Выражение \(a \leftarrow f(x)\) означает, что переменная a получает новое значение: результат \(f(x)\). Мы говорим, что переменной a присваивается новое значение. Аналогично, \(\mathbf{a} \leftarrow [a_1, a_2]\) означает, что векторная переменная a получает двумерное векторное значение \([a_1, a_2]\).
2.1.9 Производная и градиент
Производная \(f'\) функции f — это функция или значение, которое описывает, насколько быстро f растет (или убывает). Если производная является постоянным значением, например 5 или -3, то функция растет (или убывает) постоянно в любой точке x своей области определения. Если производная \(f'\) является функцией, то функция f может расти с разной скоростью в разных областях своей области определения. Если производная \(f'\) положительна в некоторой точке x, то функция f растет в этой точке. Если производная f отрицательна в некоторой точке x, то функция убывает в этой точке. Нулевая производная в точке x означает, что наклон функции в точке x горизонтальный.
Процесс нахождения производной называется дифференцированием.
Производные для основных функций известны. Например, если \(f(x) = x^2\), то \(f'(x) = 2x\); если \(f(x) = 2x\), то \(f'(x) = 2\); если \(f(x) = 2\), то \(f'(x) = 0\) (производная любой функции \(f(x) = c\), где c — постоянное значение, равна нулю).
Если функция, которую мы хотим дифференцировать, не является основной, мы можем найти ее производную, используя правило цепочки (chain rule). Например, если \(F(x) = f(g(x))\), где f и g — некоторые функции, то \(F'(x) = f'(g(x))g'(x)\). Например, если \(F(x) = (5x + 1)^2\), то \(g(x) = 5x + 1\) и \(f(g(x)) = (g(x))^2\). Применяя правило цепочки, мы находим \(F'(x) = 2(5x + 1)g'(x) = 2(5x + 1)5 = 50x + 10\).
Градиент — это обобщение производной для функций, которые принимают несколько входов (или один вход в виде вектора или какой-либо другой сложной структуры). Градиент функции — это вектор частных производных. Нахождение частной производной функции можно рассматривать как процесс нахождения производной, фокусируясь на одном из входов функции и рассматривая все остальные входы как постоянные значения.
Например, если наша функция определена как \(f([x^{(1)}, x^{(2)}]) = ax^{(1)} + bx^{(2)} + c\), то частная производная функции f по \(x^{(1)}\), обозначаемая как \(\frac{\partial f}{\partial x^{(1)}}\), задается,
\[ \frac{\partial f}{\partial x^{(1)}} = a + 0 + 0 = a, \]где a — производная функции \(ax^{(1)}\); два нуля — это соответственно производные \(bx^{(2)}\) и c, потому что \(x^{(2)}\) считается постоянной, когда мы вычисляем производную по \(x^{(1)}\), а производная любой константы равна нулю.
Аналогично, частная производная функции f по \(x^{(2)}\), \(\frac{\partial f}{\partial x^{(2)}}\), задается,
\[ \frac{\partial f}{\partial x^{(2)}} = 0 + b + 0 = b. \]Градиент функции f, обозначаемый как \(\nabla f\), задается вектором \([\frac{\partial f}{\partial x^{(1)}}, \frac{\partial f}{\partial x^{(2)}}]\).
Правило цепочки работает и с частными производными, как я иллюстрирую в Главе 4.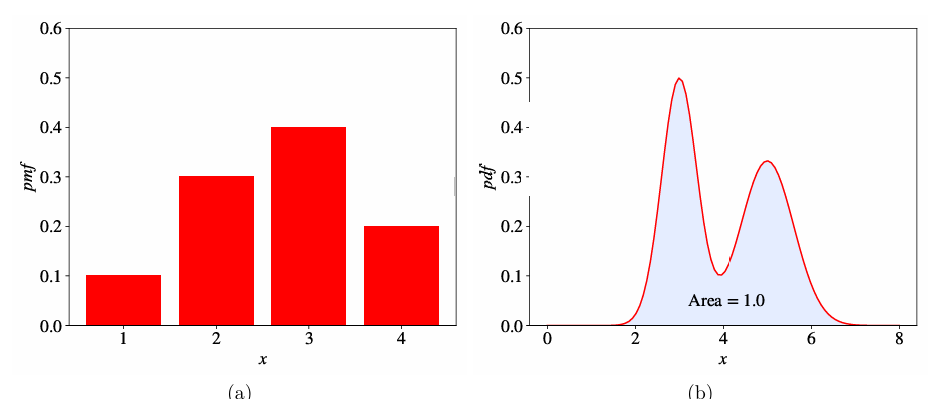
2.2 Случайная величина
Случайная величина, обычно записываемая как курсивная заглавная буква, например X, — это переменная, возможные значения которой являются числовыми исходами случайного явления. Примеры случайных явлений с числовым исходом включают бросок монеты (0 для орла и 1 для решки), бросок игральной кости или рост первого встреченного вами незнакомца на улице. Существует два типа случайных величин: дискретные и непрерывные.
Дискретная случайная величина принимает только счетное число различных значений, таких как красный, желтый, синий или 1, 2, 3, ....
Распределение вероятностей дискретной случайной величины описывается списком вероятностей, связанных с каждым из ее возможных значений. Этот список вероятностей называется функцией вероятности (probability mass function - pmf). Например: Pr(X = красный) = 0.3, Pr(X = желтый) = 0.45, Pr(X = синий) = 0.25. Каждая вероятность в функции вероятности — это значение, большее или равное 0. Сумма вероятностей равна 1 (Рисунок 3a в pdf).
Непрерывная случайная величина (CRV) принимает бесконечное число возможных значений в некотором интервале. Примеры включают рост, вес и время. Поскольку число значений непрерывной случайной величины X бесконечно, вероятность Pr(X = c) для любого c равна 0. Поэтому вместо списка вероятностей распределение вероятностей CRV (непрерывное распределение вероятностей) описывается функцией плотности вероятности (probability density function - pdf). Pdf — это функция, область значений которой неотрицательна, а площадь под кривой равна 1 (Рисунок 3b в pdf).
Пусть дискретная случайная величина X имеет k возможных значений \({x_i}_{i=1}^k\). Математическое ожидание X, обозначаемое как E[X], задается,
\[ E[X] \stackrel{\text{def}}{=} \sum_{i=1}^k [x_i \cdot \text{Pr}(X = x_i)] = x_1 \cdot \text{Pr}(X = x_1) + x_2 \cdot \text{Pr}(X = x_2) + \dots + x_k \cdot \text{Pr}(X = x_k), \quad (1) \]где Pr(X = xi) — это вероятность того, что X имеет значение xi согласно pmf. Математическое ожидание случайной величины также называется средним (mean), средним значением (average) или ожидаемым значением (expected value) и часто обозначается буквой \(\mu\). Математическое ожидание — одна из самых важных статистик случайной величины.
Другой важной статистикой является стандартное отклонение, определяемое как,
\[ \sigma \stackrel{\text{def}}{=} \sqrt{E[(X - \mu)^2]}. \]Дисперсия, обозначаемая как \(\sigma^2\) или var(X), определяется как,
\[ \sigma^2 = E[(X - \mu)^2]. \]Для дискретной случайной величины стандартное отклонение задается:
\[ \sigma = \sqrt{\text{Pr}(X = x_1)(x_1 - \mu)^2 + \text{Pr}(X = x_2)(x_2 - \mu)^2 + \dots + \text{Pr}(X = x_k)(x_k - \mu)^2}, \]где \(\mu = E[X]\).
Математическое ожидание непрерывной случайной величины X задается,
\[ E[X] \stackrel{\text{def}}{=} \int_{\mathbb{R}} xf_X(x) dx, \quad (2) \]где \(f_X\) — это pdf переменной X, а \(\int_{\mathbb{R}}\) — интеграл функции \(xf_X\).
Интеграл является эквивалентом суммирования по всем значениям функции, когда функция имеет непрерывную область определения. Он равен площади под кривой функции. Свойство pdf, заключающееся в том, что площадь под ее кривой равна 1, математически означает, что \(\int_{\mathbb{R}} f_X(x) dx = 1\).
Большую часть времени мы не знаем \(f_X\), но мы можем наблюдать некоторые значения X. В машинном обучении мы называем эти значения примерами (examples), а совокупность этих примеров называется выборкой (sample) или набором данных (dataset).
2.3 Несмещенные оценки
Поскольку \(f_X\) обычно неизвестна, но у нас есть выборка \(\mathcal{S}_X = \{x_i\}_{i=1}^N\), мы часто довольствуемся не истинными значениями статистик распределения вероятностей, таких как математическое ожидание, а их несмещенными оценками (unbiased estimators).
Мы говорим, что \(\hat{\theta}(\mathcal{S}_X)\) является несмещенной оценкой некоторой статистики \(\theta\), вычисленной с использованием выборки \(\mathcal{S}_X\), взятой из неизвестного распределения вероятностей, если \(\hat{\theta}(\mathcal{S}_X)\) обладает следующим свойством:
\[ E[\hat{\theta}(\mathcal{S}_X)] = \theta, \]где \(\hat{\theta}\) — это выборочная статистика, полученная с использованием выборки \(\mathcal{S}_X\), а не реальная статистика \(\theta\), которую можно получить, только зная \(f_X\); математическое ожидание берется по всем возможным выборкам, взятым из X. Интуитивно это означает, что если вы можете иметь неограниченное количество таких выборок, как \(\mathcal{S}_X\), и вы вычисляете некоторую несмещенную оценку, такую как \(\hat{\mu}\), используя каждую выборку, то среднее значение всех этих \(\hat{\mu}\) равно реальной статистике \(\mu\), которую вы получили бы, вычислив ее на X.
Можно показать, что несмещенной оценкой неизвестного E[X] (заданного либо ур. 1, либо ур. 2) является \(\frac{1}{N}\sum_{i=1}^N x_i\) (называемая в статистике выборочным средним (sample mean)).
2.4 Правило Байеса
Условная вероятность Pr(X = x|Y = y) — это вероятность того, что случайная величина X примет конкретное значение x при условии, что другая случайная величина Y имеет конкретное значение y. Правило Байеса (также известное как теорема Байеса) гласит, что:
\[ \text{Pr}(X = x|Y = y) = \frac{\text{Pr}(Y = y|X = x) \text{Pr}(X = x)}{\text{Pr}(Y = y)}. \]2.5 Оценка параметров
Правило Байеса полезно, когда у нас есть модель распределения X, и эта модель \(f_{\boldsymbol{\theta}}\) является функцией, имеющей некоторые параметры в виде вектора \(\boldsymbol{\theta}\). Примером такой функции может быть функция Гаусса, которая имеет два параметра, \(\mu\) и \(\sigma\), и определяется как:
\[ f_{\boldsymbol{\theta}}(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad (3) \]где \(\boldsymbol{\theta} \stackrel{\text{def}}{=} [\mu, \sigma]\), а \(\pi\) — константа (3.14159...).
Эта функция обладает всеми свойствами pdf1. Следовательно, мы можем использовать ее как модель неизвестного распределения X. Мы можем обновлять значения параметров в векторе \(\boldsymbol{\theta}\) из данных, используя правило Байеса:
\[ \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}|X = x) \leftarrow \frac{\text{Pr}(X = x|\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}) \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}})}{\text{Pr}(X = x)} = \frac{\text{Pr}(X = x|\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}) \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}})}{\sum_{\tilde{\boldsymbol{\theta}}} \text{Pr}(X = x|\boldsymbol{\theta} = \tilde{\boldsymbol{\theta}}) \text{Pr}(\boldsymbol{\theta} = \tilde{\boldsymbol{\theta}})}. \quad (4) \]где \(\text{Pr}(X = x|\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}) \stackrel{\text{def}}{=} f_{\hat{\boldsymbol{\theta}}}\).
Если у нас есть выборка \(\mathcal{S}\) из X и множество возможных значений для \(\boldsymbol{\theta}\) конечно, мы можем легко оценить \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}})\), применяя правило Байеса итеративно, по одному примеру \(x \in \mathcal{S}\) за раз. Начальное значение \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}})\) можно предположить таким образом, что \(\sum_{\hat{\boldsymbol{\theta}}} \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}) = 1\). Это предположение о вероятностях для разных \(\hat{\boldsymbol{\theta}}\) называется априорным (prior).
Сначала мы вычисляем \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}|X = x_1)\) для всех возможных значений \(\hat{\boldsymbol{\theta}}\). Затем, перед повторным обновлением \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}|X = x)\), на этот раз для \(x = x_2 \in \mathcal{S}\) с использованием ур. 4, мы заменяем априорное \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}})\) в ур. 4 новой оценкой \(\text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}) \leftarrow \frac{1}{N} \sum_{x \in \mathcal{S}} \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}|X = x)\).
Наилучшее значение параметров \(\boldsymbol{\theta}^*\) для данного одного примера получается с использованием принципа максимума апостериорной вероятности (maximum a posteriori - MAP):
\[ \boldsymbol{\theta}^* = \arg \max_{\boldsymbol{\theta}} \prod_{i=1}^N \text{Pr}(\boldsymbol{\theta} = \hat{\boldsymbol{\theta}}|X = x_i). \quad (5) \]Если множество возможных значений для \(\boldsymbol{\theta}\) не конечно, то нам нужно оптимизировать ур. 5 напрямую, используя процедуру численной оптимизации, такую как градиентный спуск, которую мы рассмотрим в Главе 4. Обычно мы оптимизируем натуральный логарифм выражения в правой части ур. 5, потому что логарифм произведения становится суммой логарифмов, и машине легче работать с суммой, чем с произведением2.
2.6 Параметры и гиперпараметры
Гиперпараметр — это свойство алгоритма обучения, обычно (но не всегда) имеющее числовое значение. Это значение влияет на то, как работает алгоритм. Гиперпараметры не изучаются алгоритмом самостоятельно из данных. Они должны быть установлены аналитиком данных перед запуском алгоритма. Я покажу, как это сделать, в Главе 5.
Параметры — это переменные, которые определяют модель, изученную алгоритмом обучения. Параметры напрямую изменяются алгоритмом обучения на основе обучающих данных. Цель обучения — найти такие значения параметров, которые делают модель оптимальной в определенном смысле.
2.7 Классификация и регрессия
Классификация — это задача автоматического присвоения метки неразмеченному примеру. Обнаружение спама — известный пример классификации.
В машинном обучении задача классификации решается алгоритмом обучения классификации, который принимает на вход коллекцию размеченных примеров и создает модель, которая может принимать неразмеченный пример на вход и либо напрямую выводить метку, либо выводить число, которое может быть использовано аналитиком для определения метки. Примером такого числа является вероятность.
В задаче классификации метка является членом конечного множества классов. Если размер множества классов равен двум («болен»/«здоров», «спам»/«не спам»), мы говорим о бинарной классификации (также называемой биномиальной в некоторых источниках). Многоклассовая классификация (также называемая мультиномиальной) — это задача классификации с тремя или более классами3.
Хотя некоторые алгоритмы обучения естественным образом допускают более двух классов, другие по своей природе являются алгоритмами бинарной классификации. Существуют стратегии, позволяющие превратить алгоритм бинарной классификации в многоклассовый. Я расскажу об одной из них в Главе 7.
Регрессия — это задача предсказания вещественной метки (часто называемой целевой переменной (target)) для неразмеченного примера. Оценка стоимости дома на основе характеристик дома, таких как площадь, количество спален, местоположение и т.д., является известным примером регрессии.
Задача регрессии решается алгоритмом обучения регрессии, который принимает на вход коллекцию размеченных примеров и создает модель, которая может принимать неразмеченный пример на вход и выводить целевую переменную.
2.8 Обучение на основе модели и обучение на основе экземпляров
Большинство алгоритмов обучения с учителем основаны на моделях. Мы уже видели один такой алгоритм: SVM. Алгоритмы обучения на основе моделей используют обучающие данные для создания модели, которая имеет параметры, изученные на обучающих данных. В SVM двумя параметрами, которые мы видели, были \(w^*\) и \(b^*\). После построения модели обучающие данные могут быть отброшены.
Алгоритмы обучения на основе экземпляров используют весь набор данных в качестве модели. Одним из часто используемых на практике алгоритмов на основе экземпляров является k-ближайших соседей (k-Nearest Neighbors - kNN). В классификации, чтобы предсказать метку для входного примера, алгоритм kNN рассматривает близкое соседство входного примера в пространстве векторов признаков и выводит метку, которую он видел чаще всего в этом близком соседстве.
2.9 Поверхностное и глубокое обучение
Поверхностный (shallow) алгоритм обучения изучает параметры модели непосредственно из признаков обучающих примеров. Большинство алгоритмов обучения с учителем являются поверхностными. Известными исключениями являются алгоритмы обучения нейронных сетей, в частности те, которые строят нейронные сети с более чем одним слоем между входом и выходом. Такие нейронные сети называются глубокими нейронными сетями (deep neural networks). В обучении глубоких нейронных сетей (или, проще говоря, глубоком обучении (deep learning)), в отличие от поверхностного обучения, большинство параметров модели изучаются не непосредственно из признаков обучающих примеров, а из выходов предыдущих слоев.
Не беспокойтесь, если вы сейчас не понимаете, что это значит. Мы рассмотрим нейронные сети более подробно в Главе 6.
1 На самом деле, ур. 3 определяет pdf одного из наиболее часто используемых на практике распределений вероятностей, называемого распределением Гаусса или нормальным распределением и обозначаемого как \(\mathcal{N}(\mu, \sigma^2)\).
2 Умножение многих чисел может дать либо очень малый, либо очень большой результат. Это часто приводит к проблеме числового переполнения (numerical overflow), когда машина не может хранить такие экстремальные числа в памяти.
3 Тем не менее, на каждый пример приходится только одна метка.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения