Глава 3. Фундаментальные алгоритмы
В этой главе я описываю пять алгоритмов, которые являются не только наиболее известными, но и либо очень эффективными сами по себе, либо используются в качестве строительных блоков для наиболее эффективных алгоритмов обучения.
3.1 Линейная регрессия
Линейная регрессия — это популярный алгоритм обучения регрессии, который изучает модель, представляющую собой линейную комбинацию признаков входного примера.
3.1.1 Постановка задачи
У нас есть коллекция размеченных примеров \({(x_i, y_i)}_{i=1}^N\), где \(N\) — размер коллекции, \(x_i\) — \(D\)-мерный вектор признаков примера \(i = 1, \dots, N\), \(y_i\) — вещественная1 целевая переменная, и каждый признак \(x_i^{(j)}\), \(j = 1, \dots, D\), также является вещественным числом.
Мы хотим построить модель \(f_{w,b}(x)\) как линейную комбинацию признаков примера \(x\):
\[ f_{w,b}(x) = wx + b, \quad (1) \]где \(w\) — \(D\)-мерный вектор параметров, а \(b\) — вещественное число. Обозначение \(f_{w,b}\) означает, что модель \(f\) параметризована двумя значениями: \(w\) и \(b\).
Мы будем использовать модель для предсказания неизвестного \(y\) для заданного \(x\) следующим образом: \(y \leftarrow f_{w,b}(x)\). Две модели, параметризованные двумя разными парами \((w, b)\), скорее всего, дадут два разных предсказания при применении к одному и тому же примеру. Мы хотим найти оптимальные значения \((w^*, b^*)\). Очевидно, оптимальные значения параметров определяют модель, которая делает наиболее точные предсказания.
Вы могли заметить, что форма нашей линейной модели в ур. 1 очень похожа на форму модели SVM. Единственное отличие — отсутствие оператора знака. Эти две модели действительно похожи. Однако гиперплоскость в SVM играет роль границы принятия решений: она используется для разделения двух групп примеров друг от друга. Как таковая, она должна быть как можно дальше от каждой группы.
С другой стороны, гиперплоскость в линейной регрессии выбирается так, чтобы быть как можно ближе ко всем обучающим примерам.
Вы можете понять, почему это последнее требование существенно, посмотрев на иллюстрацию на Рисунке 1 (в pdf). На нем показана линия регрессии (красным цветом) для одномерных примеров (синие точки). Мы можем использовать эту линию для предсказания значения целевой переменной \(y_{new}\) для нового неразмеченного входного примера \(x_{new}\). Если наши примеры — это \(D\)-мерные векторы признаков (при \(D > 1\)), единственное отличие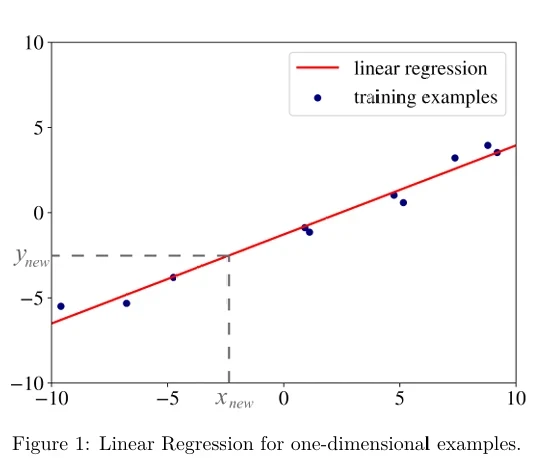
от одномерного случая заключается в том, что модель регрессии — это не линия, а плоскость (для двух измерений) или гиперплоскость (для \(D > 2\)).
Теперь вы видите, почему важно требование, чтобы гиперплоскость регрессии лежала как можно ближе к обучающим примерам: если бы красная линия на Рисунке 1 была далеко от синих точек, предсказание \(y_{new}\) имело бы меньше шансов быть правильным.
3.1.2 Решение
Чтобы удовлетворить это последнее требование, процедура оптимизации, которую мы используем для нахождения оптимальных значений \(w^*\) и \(b^*\), пытается минимизировать следующее выражение:
\[ \frac{1}{N} \sum_{i=1}^N (f_{w,b}(x_i) - y_i)^2. \quad (2) \]В математике выражение, которое мы минимизируем или максимизируем, называется целевой функцией (objective function), или просто целью (objective). Выражение \((f_{w,b}(x_i) - y_i)^2\) в приведенной выше цели называется функцией потерь (loss function). Это мера штрафа за неправильную классификацию примера \(i\). Этот конкретный выбор функции потерь называется потерей в виде квадрата ошибки (squared error loss). Все алгоритмы обучения на основе моделей имеют функцию потерь, и то, что мы делаем для нахождения наилучшей модели, — это пытаемся минимизировать цель, известную как функция стоимости (cost function). В линейной регрессии функция стоимости задается средней потерей, также называемой эмпирическим риском (empirical risk). Средняя потеря, или эмпирический риск, для модели — это среднее значение всех штрафов, полученных путем применения модели к обучающим данным.
Почему потеря в линейной регрессии является квадратичной функцией? Почему бы нам не взять абсолютное значение разницы между истинной целевой переменной \(y_i\) и предсказанным значением \(f(x_i)\) и не использовать это в качестве штрафа? Мы могли бы. Более того, мы также могли бы использовать куб вместо квадрата.
Теперь вы, вероятно, начинаете понимать, сколько, казалось бы, произвольных решений принимается при разработке алгоритма машинного обучения: мы решили использовать линейную комбинацию признаков для предсказания целевой переменной. Однако мы могли бы использовать квадрат или какой-либо другой полином для комбинирования значений признаков. Мы также могли бы использовать другую функцию потерь, которая имеет смысл: абсолютная разница между \(f(x_i)\) и \(y_i\) имеет смысл, куб разницы тоже; бинарная потеря (1, когда \(f(x_i)\) и \(y_i\) разные, и 0, когда они одинаковые) тоже имеет смысл, верно?
Если бы мы приняли другие решения относительно формы модели, формы функции потерь и выбора алгоритма, который минимизирует среднюю потерю для нахождения наилучших значений параметров, мы бы изобрели другой алгоритм машинного обучения. Звучит просто, не так ли? Однако не спешите изобретать новый алгоритм обучения. Тот факт, что он отличается, не означает, что он будет работать лучше на практике.
Люди изобретают новые алгоритмы обучения по одной из двух основных причин:
- Новый алгоритм решает конкретную практическую задачу лучше, чем существующие алгоритмы.
- Новый алгоритм имеет лучшие теоретические гарантии качества производимой им модели.
Одно из практических обоснований выбора линейной формы для модели заключается в том, что она проста. Зачем использовать сложную модель, если можно использовать простую? Другое соображение заключается в том, что линейные модели редко переобучаются (overfit). Переобучение — это свойство модели, при котором модель очень хорошо предсказывает метки примеров, использованных при обучении, но часто делает ошибки при применении к примерам, которые не были видны алгоритму обучения во время обучения.
Пример переобучения в регрессии показан на Рисунке 2 (в pdf). Данные, использованные для построения красной линии регрессии, такие же, как на Рисунке 1. Разница в том, что на этот раз это полиномиальная регрессия с полиномом степени 10. Линия регрессии почти идеально предсказывает целевые переменные почти всех обучающих примеров, но, скорее всего, сделает значительные ошибки на новых данных, как вы можете видеть на Рисунке 1 для \(x_{new}\). Мы подробнее поговорим о переобучении и о том, как его избежать, в Главе 5.
Теперь вы знаете, почему линейная регрессия может быть полезной: она не сильно переобучается. Но как насчет квадрата потерь? Почему мы решили, что он должен быть в квадрате? В 1805 году французский математик Адриен-Мари Лежандр, который первым опубликовал метод суммы квадратов для оценки качества модели, заявил, что возведение ошибки в квадрат перед суммированием удобно. Почему он так сказал? Абсолютное значение неудобно, потому что у него нет непрерывной производной, что делает функцию негладкой. Функции, которые не являются гладкими, создают ненужные трудности при использовании линейной алгебры для поиска решений задач оптимизации в замкнутой форме (closed form). Решения в замкнутой форме для нахождения оптимума функции — это простые алгебраические выражения, и они часто предпочтительнее использования сложных методов численной оптимизации, таких как градиентный спуск (используемый, среди прочего, для обучения нейронных сетей).
Интуитивно, квадратичные штрафы также выгодны, потому что они преувеличивают разницу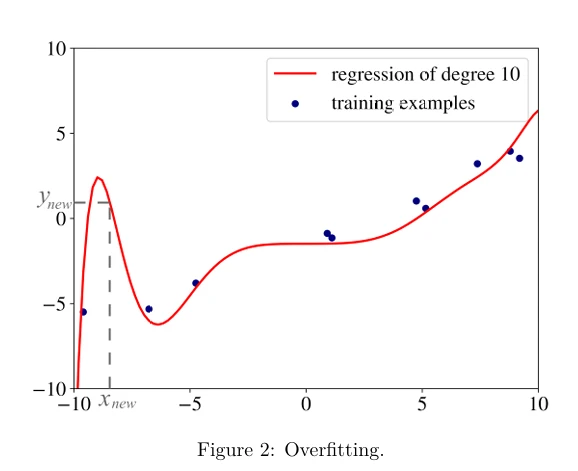
между истинной целевой переменной и предсказанной в соответствии со значением этой разницы. Мы могли бы также использовать степени 3 или 4, но их производные сложнее в работе.
Наконец, почему нас волнует производная средней потери? Если мы можем вычислить градиент функции в ур. 2, мы можем затем приравнять этот градиент к нулю2 и найти решение системы уравнений, которое дает нам оптимальные значения \(w^*\) и \(b^*\).
3.2 Логистическая регрессия
Первое, что нужно сказать, это то, что логистическая регрессия — это не регрессия, а алгоритм обучения классификации. Название происходит из статистики и связано с тем, что математическая формулировка логистической регрессии похожа на формулировку линейной регрессии.
Я объясняю логистическую регрессию на примере бинарной классификации. Однако ее можно естественным образом расширить на многоклассовую классификацию.
3.2.1 Постановка задачи
В логистической регрессии мы все еще хотим моделировать \(y_i\) как линейную функцию от \(x_i\), однако при бинарном \(y_i\) это не так просто. Линейная комбинация признаков, такая как \(wx_i + b\), — это функция, которая охватывает диапазон от минус бесконечности до плюс бесконечности, в то время как \(y_i\) имеет только два возможных значения.
В то время, когда отсутствие компьютеров требовало от ученых выполнения ручных вычислений, они стремились найти линейную модель классификации. Они поняли, что если мы определим отрицательную метку как 0, а положительную метку как 1, нам просто нужно будет найти простую непрерывную функцию, область значений которой равна (0, 1). В таком случае, если значение, возвращаемое моделью для входа \(x\), ближе к 0, мы присваиваем \(x\) отрицательную метку; в противном случае пример помечается как положительный. Одной из функций, обладающих таким свойством, является стандартная логистическая функция (также известная как сигмоидная функция (sigmoid function)):
\[ f(x) = \frac{1}{1 + e^{-x}}, \]где \(e\) — основание натурального логарифма (также называемое числом Эйлера; \(e^x\) также известна как функция \(exp(x)\) в языках программирования). Ее график изображен на Рисунке 3 (в pdf).
Модель логистической регрессии выглядит так:
\[ f_{w,b}(x) \stackrel{\text{def}}{=} \frac{1}{1 + e^{-(wx+b)}}. \quad (3) \]Вы можете видеть знакомый член \(wx + b\) из линейной регрессии.
Глядя на график стандартной логистической функции, мы видим, насколько хорошо она подходит для нашей цели классификации: если мы оптимизируем значения \(w\) и \(b\) соответствующим образом, мы можем интерпретировать выход \(f(x)\) как вероятность того, что \(y_i\) является положительным. Например, если она выше или равна порогу 0.5, мы скажем, что класс \(x\) положительный; в противном случае — отрицательный. На практике выбор порога может отличаться в зависимости от задачи. Мы вернемся к этому обсуждению в Главе 5, когда будем говорить об оценке производительности модели.
Теперь, как нам найти оптимальные \(w^*\) и \(b^*\)? В линейной регрессии мы минимизировали эмпирический риск, который был определен как средняя квадратичная ошибка потерь, также известная как среднеквадратичная ошибка (mean squared error - MSE).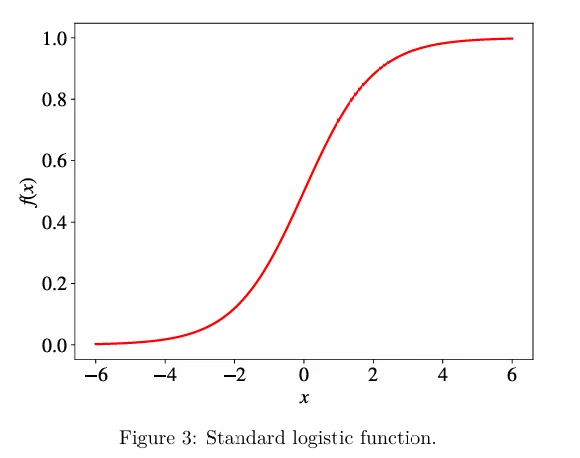
3.2.2 Решение
В логистической регрессии, с другой стороны, мы максимизируем правдоподобие (likelihood) нашего обучающего набора согласно модели. В статистике функция правдоподобия определяет, насколько вероятно наблюдение (пример) согласно нашей модели.
Например, пусть у нас есть размеченный пример \((x_i, y_i)\) в наших обучающих данных. Предположим также, что мы нашли (угадали) некоторые конкретные значения \(\hat{w}\) и \(\hat{b}\) наших параметров. Если мы теперь применим нашу модель \(f_{\hat{w},\hat{b}}\) к \(x_i\), используя ур. 3, мы получим некоторое значение \(0 < p < 1\) в качестве выхода. Если \(y_i\) — положительный класс, правдоподобие того, что \(y_i\) является положительным классом, согласно нашей модели, равно \(p\). Аналогично, если \(y_i\) — отрицательный класс, правдоподобие того, что он является отрицательным классом, равно \(1 - p\).
Критерий оптимизации в логистической регрессии называется максимальным правдоподобием (maximum likelihood). Вместо минимизации средней потери, как в линейной регрессии, мы теперь максимизируем правдоподобие обучающих данных согласно нашей модели:
\[ L_{w,b} \stackrel{\text{def}}{=} \prod_{i=1}^N f_{w,b}(x_i)^{y_i} (1 - f_{w,b}(x_i))^{(1-y_i)}. \quad (4) \]Выражение \(f_{w,b}(x)^{y_i} (1 - f_{w,b}(x))^{(1-y_i)}\) может выглядеть пугающе, но это просто причудливый математический способ сказать: «\(f_{w,b}(x)\), когда \(y_i = 1\), и \((1 - f_{w,b}(x))\) в противном случае». Действительно, если \(y_i = 1\), то \((1 - f_{w,b}(x))^{(1-y_i)}\) равно 1, потому что \((1 - y_i) = 0\), а мы знаем, что любое число в степени 0 равно 1. С другой стороны, если \(y_i = 0\), то \(f_{w,b}(x)^{y_i}\) равно 1 по той же причине.
Вы могли заметить, что мы использовали оператор произведения \(\prod\) в целевой функции вместо оператора суммы \(\sum\), который использовался в линейной регрессии. Это потому, что правдоподобие наблюдения \(N\) меток для \(N\) примеров является произведением правдоподобий каждого наблюдения (предполагая, что все наблюдения независимы друг от друга, что и имеет место). Вы можете провести параллель с умножением вероятностей исходов в серии независимых экспериментов в теории вероятностей.
Из-за функции \(exp\), используемой в модели, на практике, чтобы избежать числового переполнения, удобнее максимизировать логарифм правдоподобия (log-likelihood) вместо правдоподобия. Логарифм правдоподобия определяется следующим образом:
\[ \text{Log}L_{w,b} \stackrel{\text{def}}{=} \ln(L_{w,b}(x)) = \sum_{i=1}^N [y_i \ln f_{w,b}(x) + (1 - y_i) \ln (1 - f_{w,b}(x))]. \]Поскольку \(\ln\) является строго возрастающей функцией, максимизация этой функции эквивалентна максимизации ее аргумента, и решение этой новой задачи оптимизации совпадает с решением исходной задачи.
В отличие от линейной регрессии, для приведенной выше задачи оптимизации нет решения в замкнутой форме. Типичная процедура численной оптимизации, используемая в таких случаях, — это градиентный спуск. Мы поговорим о нем в следующей главе.
3.3 Обучение деревьев решений
Дерево решений (decision tree) — это ациклический граф, который можно использовать для принятия решений. В каждом узле ветвления графа проверяется конкретный признак \(j\) вектора признаков. Если значение признака ниже определенного порога, то переход осуществляется по левой ветви; в противном случае — по правой ветви. По достижении листового узла принимается решение о классе, к которому принадлежит пример.
Как следует из названия раздела, дерево решений можно обучить на данных.
3.3.1 Постановка задачи
Как и ранее, у нас есть коллекция размеченных примеров; метки принадлежат множеству \(\{0, 1\}\). Мы хотим построить дерево решений, которое позволит нам предсказать класс по вектору признаков.
3.3.2 Решение
Существуют различные формулировки алгоритма обучения деревьев решений. В этой книге мы рассмотрим только одну, называемую ID3.
Критерий оптимизации в данном случае — средний логарифм правдоподобия:
\[ \frac{1}{N} \sum_{i=1}^N [y_i \ln f_{ID3}(x_i) + (1 - y_i) \ln (1 - f_{ID3}(x_i))], \quad (5) \]где \(f_{ID3}\) — это дерево решений.
К настоящему моменту это выглядит очень похоже на логистическую регрессию. Однако, в отличие от алгоритма обучения логистической регрессии, который строит параметрическую модель \(f_{w^*,b^*}\), находя оптимальное решение задачи оптимизации, алгоритм ID3 оптимизирует ее приблизительно, строя непараметрическую модель \(f_{ID3}(x) \stackrel{\text{def}}{=} \text{Pr}(y = 1|x)\).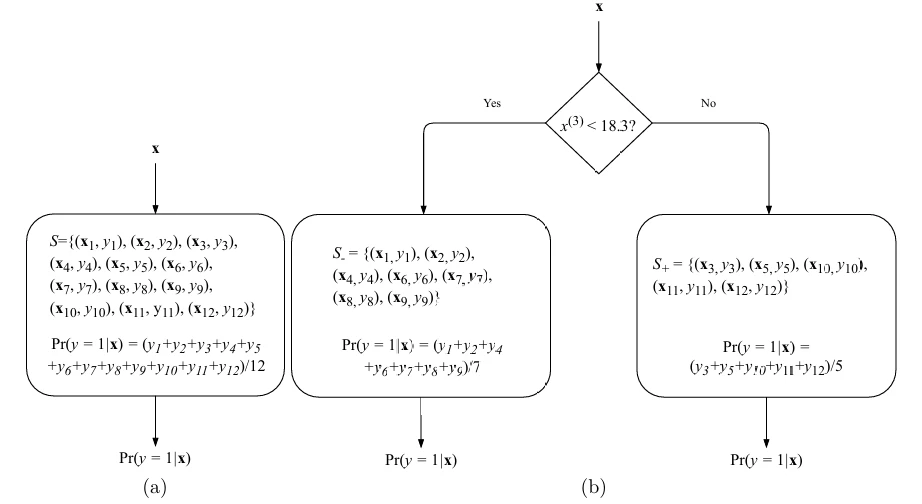
Алгоритм обучения ID3 работает следующим образом. Пусть \(\mathcal{S}\) обозначает множество размеченных примеров. В начале дерево решений имеет только стартовый узел, который содержит все примеры: \(\mathcal{S} \stackrel{\text{def}}{=} \{(x_i, y_i)\}_{i=1}^N\). Начнем с постоянной модели \(f^{\mathcal{S}}_{ID3}\), определяемой как,
\[ f^{\mathcal{S}}_{ID3} \stackrel{\text{def}}{=} \frac{1}{|\mathcal{S}|} \sum_{(x,y) \in \mathcal{S}} y. \quad (6) \]Предсказание, выдаваемое приведенной выше моделью, \(f^{\mathcal{S}}_{ID3}(x)\), будет одинаковым для любого входа \(x\). Соответствующее дерево решений, построенное с использованием игрушечного набора данных из 12 размеченных примеров, показано на Рисунке 4a (в pdf).
Затем мы ищем по всем признакам \(j = 1, \dots, D\) и всем порогам \(t\) и разделяем множество \(\mathcal{S}\) на два подмножества: \(\mathcal{S}^- \stackrel{\text{def}}{=} \{(x, y)|(x, y) \in \mathcal{S}, x^{(j)} < t\}\) и \(\mathcal{S}^+ \stackrel{\text{def}}{=} \{(x, y)|(x, y) \in \mathcal{S}, x^{(j)} \ge t\}\). Два новых подмножества попадут в два новых листовых узла, и мы оцениваем для всех возможных пар \((j, t)\), насколько хорошим является разделение с частями \(\mathcal{S}^-\) и \(\mathcal{S}^+\). Наконец, мы выбираем наилучшие такие значения \((j, t)\), разделяем \(\mathcal{S}\) на \(\mathcal{S}^+\) и \(\mathcal{S}^-\), формируем два новых листовых узла и продолжаем рекурсивно на \(\mathcal{S}^+\) и \(\mathcal{S}^-\) (или останавливаемся, если ни одно разделение не дает модель, которая значительно лучше текущей). Дерево решений после одного разделения иллюстрируется на Рисунке 4b (в pdf).
Теперь вам должно быть интересно, что означают слова «оценить, насколько хорошим является разделение». В ID3 качество разделения оценивается с использованием критерия, называемого энтропией (entropy). Энтропия — это мера неопределенности случайной величины. Она достигает своего максимума, когда все значения случайной величины равновероятны. Энтропия достигает своего минимума, когда случайная величина может принимать только одно значение. Энтропия множества примеров \(\mathcal{S}\) задается,
\[ H(\mathcal{S}) \stackrel{\text{def}}{=} -f^{\mathcal{S}}_{ID3} \ln f^{\mathcal{S}}_{ID3} - (1 - f^{\mathcal{S}}_{ID3}) \ln(1 - f^{\mathcal{S}}_{ID3}). \quad (7) \]Когда мы разделяем множество примеров по определенному признаку \(j\) и порогу \(t\), энтропия разделения, \(H(\mathcal{S}^-, \mathcal{S}^+)\), — это просто взвешенная сумма двух энтропий:
\[ H(\mathcal{S}^-, \mathcal{S}^+) \stackrel{\text{def}}{=} \frac{|\mathcal{S}^-|}{|\mathcal{S}|} H(\mathcal{S}^-) + \frac{|\mathcal{S}^+|}{|\mathcal{S}|} H(\mathcal{S}^+). \quad (8) \]Таким образом, в ID3 на каждом шаге, в каждом листовом узле мы находим разделение, которое минимизирует энтропию, заданную ур. 8, или останавливаемся в этом листовом узле.
Алгоритм останавливается в листовом узле в любой из следующих ситуаций:
- Все примеры в листовом узле классифицируются правильно однокомпонентной моделью (ур. 6).
- Мы не можем найти атрибут для разделения.
- Разделение уменьшает энтропию менее чем на некоторое \(\epsilon\) (значение которого должно быть найдено экспериментально3).
- Дерево достигает некоторой максимальной глубины \(d\) (также должна быть найдена экспериментально).
Поскольку в ID3 решение о разделении набора данных на каждой итерации является локальным (не зависит от будущих разделений), алгоритм не гарантирует оптимального решения. Модель может быть
улучшена с использованием методов, таких как поиск с возвратом (backtracking) во время поиска оптимального дерева решений, ценой возможного увеличения времени построения модели.
Наиболее широко используемая формулировка алгоритма обучения деревьев решений называется C4.5. Он имеет несколько дополнительных функций по сравнению с ID3:
- он принимает как непрерывные, так и дискретные признаки;
- он обрабатывает неполные примеры;
- он решает проблему переобучения, используя технику снизу вверх, известную как «обрезка» (pruning).
Обрезка заключается в проходе по дереву после его создания и удалении ветвей, которые не вносят достаточно значимого вклада в снижение ошибки, заменяя их листовыми узлами.
Критерий разделения на основе энтропии интуитивно понятен: энтропия достигает своего минимума 0, когда все примеры в \(\mathcal{S}\) имеют одинаковую метку; с другой стороны, энтропия максимальна и равна 1, когда ровно половина примеров в \(\mathcal{S}\) помечена 1, что делает такой лист бесполезным для классификации. Единственный оставшийся вопрос заключается в том, как этот алгоритм приблизительно максимизирует критерий среднего логарифма правдоподобия. Я оставляю это для дальнейшего чтения.
3.4 Метод опорных векторов
Я уже представлял SVM во введении, поэтому этот раздел лишь заполняет пару пробелов. Необходимо ответить на два критических вопроса:
- Что, если в данных есть шум и ни одна гиперплоскость не может идеально разделить положительные примеры от отрицательных?
- Что, если данные не могут быть разделены с помощью плоскости, но могут быть разделены полиномом более высокого порядка?
Вы можете видеть обе ситуации, изображенные на Рисунке 5 (в pdf). В левом случае данные могли бы быть разделены прямой линией, если бы не шум (выбросы или примеры с неправильными метками). В правом случае граница принятия решений — это круг, а не прямая линия.
Помните, что в SVM мы хотим удовлетворить следующие ограничения:
\begin{align*} wx_i - b \ge +1 & \quad \text{если } y_i = +1, \\ wx_i - b \le -1 & \quad \text{если } y_i = -1. \quad (9) \end{align*}Мы также хотим минимизировать \(\|w\|\), чтобы гиперплоскость была равноудалена от ближайших примеров каждого класса. Минимизация \(\|w\|\) эквивалентна минимизации \(\frac{1}{2}\|w\|^2\), и использование этого члена позволяет выполнить оптимизацию квадратичного программирования позже. Задача оптимизации для SVM, следовательно, выглядит так: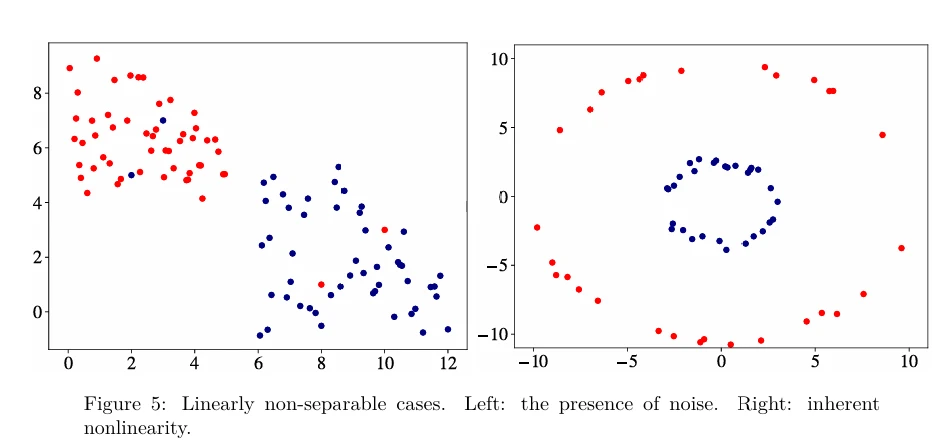
3.4.1 Работа с шумом
Чтобы расширить SVM на случаи, когда данные не являются линейно разделимыми, мы вводим шарнирную функцию потерь (hinge loss function): \(\max(0, 1 - y_i(wx_i - b))\).
Шарнирная функция потерь равна нулю, если ограничения в ур. 9 удовлетворены; другими словами, если \(wx_i\) лежит на правильной стороне границы принятия решений. Для данных на неправильной стороне границы принятия решений значение функции пропорционально расстоянию от границы принятия решений.
Затем мы хотим минимизировать следующую функцию стоимости,
\[ C\|w\|^2 + \frac{1}{N} \sum_{i=1}^N \max(0, 1 - y_i(wx_i - b)), \]где гиперпараметр \(C\) определяет компромисс между увеличением размера границы принятия решений и обеспечением того, чтобы каждый \(x_i\) лежал на правильной стороне границы принятия решений. Значение \(C\) обычно выбирается экспериментально, так же как гиперпараметры \(\epsilon\) и \(d\) в ID3. SVM, которые оптимизируют шарнирную потерю, называются SVM с мягким зазором (soft-margin SVMs), в то время как исходная формулировка называется SVM с жестким зазором (hard-margin SVM).
Как вы можете видеть, при достаточно высоких значениях \(C\) второй член в функции стоимости станет незначительным, поэтому алгоритм SVM попытается найти наибольший зазор, полностью
игнорируя неправильную классификацию. По мере уменьшения значения \(C\) совершение ошибок классификации становится все более дорогостоящим, поэтому алгоритм SVM пытается сделать меньше ошибок, жертвуя размером зазора. Как мы уже обсуждали, больший зазор лучше для обобщения. Следовательно, \(C\) регулирует компромисс между хорошей классификацией обучающих данных (минимизация эмпирического риска) и хорошей классификацией будущих примеров (обобщение).
3.4.2 Работа с внутренней нелинейностью
SVM можно адаптировать для работы с наборами данных, которые не могут быть разделены гиперплоскостью в их исходном пространстве. Действительно, если нам удастся преобразовать исходное пространство в пространство более высокой размерности, мы можем надеяться, что примеры станут линейно разделимыми в этом преобразованном пространстве. В SVM использование функции для неявного преобразования исходного пространства в пространство более высокой размерности во время оптимизации функции стоимости называется ядерным трюком (kernel trick).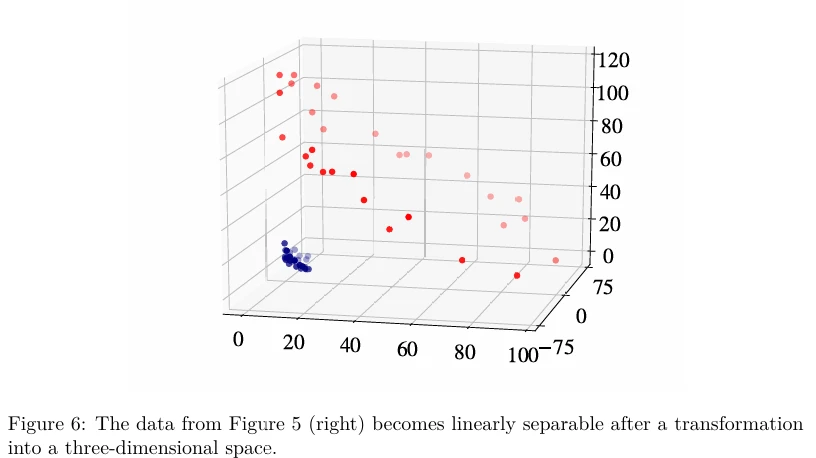
Эффект применения ядерного трюка иллюстрируется на Рисунке 6 (в pdf). Как вы можете видеть, возможно преобразовать двумерные нелинейно разделимые данные в линейно разделимые трехмерные данные с помощью конкретного отображения \(\phi: x \to \phi(x)\), где \(\phi(x)\) — вектор более высокой размерности, чем \(x\). Для примера 2D-данных на Рисунке 5 (справа) отображение \(\phi\), которое проецирует 2D-пример \(x = [q, p]\) в 3D-пространство (Рисунок 6), будет выглядеть так: \(\phi([q, p]) \stackrel{\text{def}}{=} (q^2, \sqrt{2qp}, p^2)\), где \(\cdot^2\) означает возведение в квадрат. Теперь вы видите, что данные становятся линейно разделимыми в преобразованном пространстве.
Однако мы не знаем априори, какое отображение \(\phi\) сработает для наших данных. Если мы сначала преобразуем все наши входные примеры, используя некоторое отображение, в векторы очень высокой размерности, а затем применим SVM к этим данным, и попробуем все возможные функции отображения, вычисления могут стать очень неэффективными, и мы никогда не решим нашу задачу классификации.
К счастью, ученые выяснили, как использовать ядерные функции (kernel functions) (или просто ядра (kernels)) для эффективной работы в пространствах более высокой размерности, не выполняя это преобразование явно. Чтобы понять, как работают ядра, мы должны сначала увидеть, как алгоритм оптимизации для SVM находит оптимальные значения для \(w\) и \(b\).
Метод, традиционно используемый для решения задачи оптимизации в ур. 10, — это метод множителей Лагранжа (Lagrange multipliers). Вместо решения исходной задачи из ур. 10 удобно решить эквивалентную задачу, сформулированную следующим образом:
\[ \max_{\alpha_1 \dots \alpha_N} \left( \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{k=1}^N y_i \alpha_i (x_i x_k) y_k \alpha_k \right) \quad \text{при условии } \sum_{i=1}^N \alpha_i y_i = 0 \text{ и } \alpha_i \ge 0, i = 1, \dots, N, \quad (11) \]где \(\alpha_i\) называются множителями Лагранжа. При такой формулировке задача оптимизации становится выпуклой задачей квадратичного программирования, эффективно решаемой алгоритмами квадратичного программирования.
Теперь вы могли заметить, что в приведенной выше формулировке есть член \(x_i x_k\), и это единственное место, где используются векторы признаков. Если мы хотим преобразовать наше векторное пространство в пространство более высокой размерности, нам нужно преобразовать \(x_i\) в \(\phi(x_i)\) и \(x_k\) в \(\phi(x_k)\), а затем перемножить \(\phi(x_i)\) и \(\phi(x_k)\). Это было бы очень дорого.
С другой стороны, нас интересует только результат скалярного произведения \(x_i x_k\), который, как мы знаем, является вещественным числом. Нам не важно, как это число было получено, лишь бы оно было правильным. Используя ядерный трюк, мы можем избавиться от дорогостоящего преобразования исходных векторов признаков в векторы более высокой размерности и избежать вычисления их скалярного произведения. Мы заменяем это простой операцией над исходными векторами признаков, которая дает тот же результат. Например, вместо преобразования \((q_1, p_1)\) в \((q_1^2, \sqrt{2q_1p_1}, p_1^2)\) и \((q_2, p_2)\) в \((q_2^2, \sqrt{2q_2p_2}, p_2^2)\), а затем вычисления скалярного произведения \((q_1^2, \sqrt{2q_1p_1}, p_1^2)\) и \((q_2^2, \sqrt{2q_2p_2}, p_2^2)\), чтобы получить \((q_1^2 q_2^2 + 2q_1q_2p_1p_2 + p_1^2 p_2^2)\), мы могли бы найти скалярное произведение между \((q_1, p_1)\) и \((q_2, p_2)\), чтобы получить \((q_1q_2 + p_1p_2)\), а затем возвести его в квадрат, чтобы получить точно такой же результат \((q_1^2 q_2^2 + 2q_1q_2p_1p_2 + p_1^2 p_2^2)\).
Это был пример ядерного трюка, и мы использовали квадратичное ядро \(k(x_i, x_k) \stackrel{\text{def}}{=} (x_i x_k)^2\). Существует множество ядерных функций, наиболее широко используемой из которых является ядро RBF (RBF kernel):
\[ k(x, x') = \exp\left(-\frac{\|x - x'\|^2}{2\sigma^2}\right), \]где \(\|x - x'\|^2\) — это квадрат евклидова расстояния (Euclidean distance) между двумя векторами признаков. Евклидово расстояние задается следующим уравнением:
\[ d(x_i, x_k) \stackrel{\text{def}}{=} \sqrt{(x_i^{(1)} - x_k^{(1)})^2 + (x_i^{(2)} - x_k^{(2)})^2 + \dots + (x_i^{(D)} - x_k^{(D)})^2} = \sqrt{\sum_{j=1}^D (x_i^{(j)} - x_k^{(j)})^2}. \]Можно показать, что пространство признаков ядра RBF (от «radial basis function» — радиально-базисная функция) имеет бесконечное число измерений. Варьируя гиперпараметр \(\sigma\), аналитик данных может выбирать между получением гладкой или извилистой границы принятия решений в исходном пространстве.
3.5 k-ближайших соседей
k-ближайших соседей (k-Nearest Neighbors - kNN) — это непараметрический алгоритм обучения. В отличие от других алгоритмов обучения, которые позволяют отбросить обучающие данные после построения модели, kNN хранит все обучающие примеры в памяти. Как только поступает новый, ранее невиданный пример \(x\), алгоритм kNN находит \(k\) обучающих примеров, ближайших к \(x\), и возвращает метку большинства, в случае классификации, или среднюю метку, в случае регрессии.
Близость двух примеров задается функцией расстояния. Например, евклидово расстояние, рассмотренное выше, часто используется на практике. Другим популярным выбором функции расстояния является отрицательное косинусное сходство (cosine similarity). Косинусное сходство, определяемое как,
\[ s(x_i, x_k) \stackrel{\text{def}}{=} \cos(\angle(x_i, x_k)) = \frac{\sum_{j=1}^D x_i^{(j)} x_k^{(j)}}{\sqrt{\sum_{j=1}^D (x_i^{(j)})^2} \sqrt{\sum_{j=1}^D (x_k^{(j)})^2}}, \]является мерой сходства направлений двух векторов. Если угол между двумя векторами равен 0 градусов, то два вектора указывают в одном направлении, и косинусное сходство равно 1. Если векторы ортогональны, косинусное сходство равно 0. Для векторов, указывающих в противоположных направлениях, косинусное сходство равно -1. Если мы хотим использовать косинусное сходство как метрику расстояния, нам нужно умножить его на -1. Другие популярные метрики расстояния включают расстояние Чебышева, расстояние Махаланобиса и расстояние Хэмминга. Выбор метрики расстояния, а также значение \(k\), — это выбор, который аналитик делает перед запуском алгоритма. Таким образом, это гиперпараметры. Метрика расстояния также может быть изучена из данных (в отличие от ее угадывания). Мы поговорим об этом в Главе 10.
1Чтобы сказать, что \(y_i\) вещественнозначное, мы пишем \(y_i \in \mathbb{R}\), где \(\mathbb{R}\) обозначает множество всех вещественных чисел, бесконечное множество чисел от минус бесконечности до плюс бесконечности.
2Чтобы найти минимум или максимум функции, мы приравниваем градиент к нулю, потому что значение градиента в экстремумах функции всегда равно нулю. В 2D градиент в экстремуме — это горизонтальная линия.
3В Главе 5 я покажу, как это сделать, в разделе о настройке гиперпараметров.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения