Маленькая книга о глубоком обучении

Часть I
Основы

Предисловие

Текущий период прогресса в области искусственного интеллекта начался, когда Крижевский и соавт. [2012] продемонстрировали, что искусственная нейронная сеть, разработанная двадцатью годами ранее [LeCun et al., 1989], может значительно превзойти сложные современные методы распознавания изображений, будучи всего лишь в сто раз крупнее и обученной на аналогично увеличенном наборе данных.

Этот прорыв стал возможным благодаря графическим процессорам (GPU) — высокопараллельным вычислительным устройствам потребительского класса, разработанным для синтеза изображений в реальном времени и перепрофилированным для искусственных нейронных сетей.

С тех пор под общим названием «глубокое обучение» инновации в структурах этих сетей, стратегии их обучения и специализированное аппаратное обеспечение позволили экспоненциально увеличить как их размер, так и количество обучающих данных, которые они используют [Sevilla et al., 2022]. Это привело к волне успешных приложений в различных технических областях, от компьютерного зрения и робототехники до обработки речи, а с 2020 года — к разработке больших языковых моделей с общими возможностями прото-рассуждения [Chowdhery et al., 2022].

Хотя большая часть глубокого обучения несложна для понимания, она объединяет разнообразные компоненты, такие как линейная алгебра, исчисление, теория вероятностей, оптимизация, обработка сигналов, программирование, алгоритмика и высокопроизводительные вычисления, что делает ее сложной для изучения.

Вместо того чтобы быть исчерпывающей, эта маленькая книга ограничивается необходимым фоном для понимания нескольких важных моделей. Этот подход оказался популярным, что привело к более чем 500 000 загрузок PDF-файла за 12 месяцев после его анонса в Twitter.

Если вы не получили эту книгу с ее официального URL

https://fleuret.org/public/lbdl.pdf

пожалуйста, сделайте это, чтобы помочь оценить количество читателей.

Франсуа Флёре,

19 мая 2024 г.

Глава 1
Машинное обучение

Глубокое обучение исторически относится к более широкой области статистического машинного обучения, поскольку фундаментально касается методов, способных изучать представления данных. Использованные методы первоначально происходят из искусственных нейронных сетей, а квалификатор «глубокое» подчеркивает, что модели представляют собой длинные композиции отображений, которые, как теперь известно, достигают большей производительности.

Модульность, универсальность и масштабируемость глубоких моделей привели к появлению множества специфических математических методов и инструментов разработки программного обеспечения, сделав глубокое обучение отдельной и обширной технической областью.

1.1 Обучение по данным

Простейший случай использования модели, обученной на данных, — это когда доступен сигнал x, например, изображение номерного знака, по которому нужно предсказать величину y, например, строку символов, написанных на знаке.

Во многих реальных ситуациях, когда x — это высокоразмерный сигнал, полученный в неконтролируемой среде, слишком сложно придумать аналитический рецепт, связывающий x и y.

Можно собрать большой обучающий набор \(\mathcal{D}\) пар \((x_n, y_n)\) и разработать параметрическую модель $f$. Это фрагмент компьютерного кода, который включает обучаемые параметры $w$, модулирующие его поведение, и такой, что при правильных значениях $w^*$, он является хорошим предсказателем. «Хороший» здесь означает, что если этому фрагменту кода дано значение $x$, вычисленное им значение $\hat{y}=f(x;w^*)$ является хорошей оценкой значения $y$, которое было бы связано с $x$ в обучающем наборе, если бы оно там присутствовало.

Это понятие «хорошести» обычно формализуется функцией потерь $\mathcal{L}(w)$, которая мала, когда $f(\cdot;w)$ хорошо работает на $\mathcal{D}$. Затем обучение модели заключается в вычислении значения $w^*$, которое минимизирует $\mathcal{L}(w^*)$.

1.2 Регрессия на основе базисных функций

Мы можем проиллюстрировать обучение модели в простом случае, когда $x_n$ и $y_n$ — два действительных числа, а функция потерь — это среднеквадратичная ошибка:

$$\mathcal{L}(w) = \frac{1}{N} \sum_{n=1}^N (y_n - f(x_n;w))^2 \quad (1.1)$$

и $f(\cdot;w)$ является линейной комбинацией предопределенного базиса функций $f_1,...,f_K$, с $w = (w_1,...,w_K)$:

$$f(x;w) = \sum_{k=1}^K w_k f_k(x)$$

Поскольку $f(x_n;w)$ является линейной по $w_k$, а $\mathcal{L}(w)$ является квадратичной по $f(x_n;w)$,

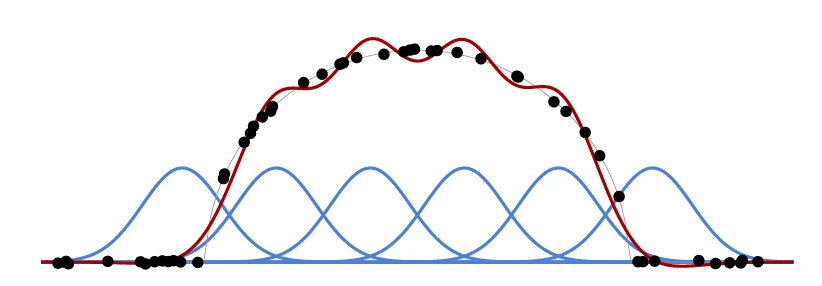
Рисунок 1.1

функция потерь $\mathcal{L}(w)$ является квадратичной по $w_k$, и нахождение $w^*$, которое ее минимизирует, сводится к решению линейной системы. См. Рисунок 1.1 для примера с гауссовыми ядрами в качестве $f_k$.

1.3 Недообучение и переобучение

Ключевым элементом является взаимодействие между емкостью модели, то есть ее гибкостью и способностью подгоняться под разнообразные данные, и объемом и качеством обучающих данных. Когда емкость недостаточна, модель не может подгоняться под данные, что приводит к высокой ошибке во время обучения. Это называется недообучением.

Напротив, когда количество данных недостаточно, как показано на Рисунке 1.2, модель часто будет изучать характеристики, специфичные для обучающих примеров, что приведет к отличной производительности во время обучения, но за счет худшего

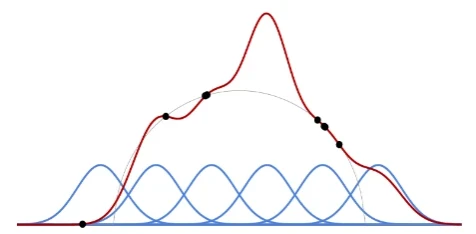
Рисунок 1.2

подгонки к глобальной структуре данных и плохой производительности на новых входных данных. Это явление называется переобучением.

Таким образом, большая часть искусства прикладного машинного обучения заключается в разработке моделей, которые не слишком гибкие, но при этом способны подгоняться под данные. Это достигается путем формирования правильного индуктивного смещения в модели, что означает, что ее структура соответствует лежащей в основе структуре данных.

Несмотря на то, что эта классическая перспектива актуальна для глубоких моделей разумного размера, ситуация становится запутанной с большими моделями, которые имеют очень большое количество обучаемых параметров и экстремальную емкость, но при этом хорошо работают на предсказании. Мы вернемся к этому в § 3.6 и § 3.7.

1.4 Категории моделей

Мы можем организовать использование моделей машинного обучения в три широкие категории:

• Регрессия заключается в предсказании непрерывнозначного вектора $y \in \mathbb{R}^K$, например, геометрического положения объекта по входному сигналу $X$. Это многомерное обобщение установки, которую мы видели в § 1.2. Обучающий набор состоит из пар входного сигнала и истинного значения.

• Классификация направлена на предсказание значения из конечного множества $\{1,...,C\}$, например, метки $Y$ изображения $X$. Как и в случае регрессии, обучающий набор состоит из пар входного сигнала и истинного значения, здесь это метка из этого множества. Стандартный способ решения этой задачи — предсказать оценку для каждого потенциального класса так, чтобы правильный класс имел максимальную оценку.

• Моделирование плотности имеет своей целью моделирование функции плотности вероятности самих данных $\mu_X$, например, изображений. В этом случае обучающий набор состоит из значений $x_n$ без связанных величин для предсказания, и обученная модель должна позволять оценивать функцию плотности вероятности или производить выборки из распределения, или и то, и другое.

Регрессия и классификация обычно называются обучением с учителем, поскольку предсказываемое значение, необходимое в качестве цели во время обучения, должно быть предоставлено, например, экспертами. Напротив, моделирование плотности обычно рассматривается как обучение без учителя, поскольку достаточно использовать имеющиеся данные без необходимости создавать связанные истинные значения.

Эти три категории не являются непересекающимися; например, классификация может быть представлена как регрессия оценок классов, или моделирование плотности дискретных последовательностей как итеративная классификация. Кроме того, они не охватывают все случаи. Может потребоваться предсказать составные величины, или несколько классов, или моделировать плотность при условии сигнала.

Глава 2
Эффективные вычисления

С точки зрения реализации глубокое обучение связано с выполнением тяжелых вычислений с большими объемами данных. Графические процессоры (GPU) сыграли важную роль в успехе этой области, позволив выполнять такие вычисления на доступном оборудовании.

Важность их использования и связанные с этим технические ограничения на вычисления, которые могут быть выполнены эффективно, вынуждают исследования в этой области постоянно балансировать между математической обоснованностью и реализуемостью новых методов.

2.1 GPU, TPU и пакеты

Графические процессоры изначально предназначались для синтеза изображений в реальном времени, что требует высокопараллельных архитектур, которые хорошо подходят для глубоких моделей. По мере увеличения их использования для ИИ, GPU стали оснащаться специализированными тензорными ядрами, и были разработаны специализированные чипы для глубокого обучения, такие как Tensor Processing Units (TPU) от Google.

GPU обладает несколькими тысячами параллельных блоков и собственной быстрой памятью. Ограничивающим фактором обычно является не количество вычислительных блоков, а операции чтения-записи в память. Самое медленное звено находится между памятью CPU и памятью GPU, и, следовательно, следует избегать копирования данных между устройствами. Более того, структура самого GPU включает несколько уровней кэш-памяти, которая меньше, но быстрее, и вычисления должны быть организованы так, чтобы избежать копирования между этими различными кэшами.

Это достигается, в частности, путем организации вычислений в пакетах образцов, которые могут полностью поместиться в память GPU и обрабатываются параллельно. Когда оператор комбинирует образец и параметры модели, оба должны быть перемещены в кэш-память рядом с фактическим вычислительным

блоками. Обработка пакетами позволяет копировать параметры модели только один раз, вместо того чтобы делать это для каждого образца. На практике GPU обрабатывает пакет, который помещается в память, почти так же быстро, как обрабатывает один образец.

Стандартный GPU имеет теоретическую пиковую производительность 10¹³–10¹⁴ операций с плавающей запятой (FLOPs) в секунду, а объем его памяти обычно варьируется от 8 до 80 гигабайт. Стандартное кодирование чисел с плавающей запятой FP32 использует 32 бита, но эмпирические результаты показывают, что использование кодирования на 16 бит, или даже меньше для некоторых операндов, не ухудшает производительность.

Мы вернемся к большому размеру глубоких архитектур в § 3.7.

2.2 Тензоры

GPU и фреймворки глубокого обучения, такие как PyTorch или JAX, манипулируют величинами для обработки, организуя их в виде тензоров, которые представляют собой наборы скаляров, расположенных вдоль нескольких дискретных осей. Они являются элементами из $\mathbb{R}^{N_1 \times \cdots \times N_D}$, обобщающими понятия вектора и матрицы.

Тензоры используются для представления как обрабатываемых сигналов, так и обучаемых параметров моделей и промежуточных величин, которые они вычисляют. Последние называются активациями, по аналогии с нейронными активациями.

Например, временной ряд естественным образом кодируется как тензор $T \times D$, или, по историческим причинам, как тензор $D \times T$, где $T$ — его длительность, а $D$ — размерность представления признаков на каждом временном шаге, часто называемая количеством каналов. Аналогично, 2D-структурированный сигнал может быть представлен как тензор $D \times H \times W$, где $H$ и $W$ — его высота и ширина. RGB-изображение будет соответствовать $D = 3$, но количество каналов может вырасти до нескольких тысяч в больших моделях.

Добавление дополнительных измерений позволяет представлять серии объектов. Например, пятьдесят RGB-изображений разрешением $32 \times 24$ могут быть закодированы как

тензор $50 \times 3 \times 24 \times 32$.

Библиотеки глубокого обучения предоставляют большое количество операций, включающих стандартную линейную алгебру, сложное изменение формы и извлечение, а также специфические для глубокого обучения операции, некоторые из которых мы увидим в Главе 4. Реализация тензоров отделяет представление формы от расположения коэффициентов в памяти, что позволяет выполнять множество операций изменения формы, транспонирования и извлечения без копирования коэффициентов, следовательно, чрезвычайно быстро.

На практике, практически любое вычисление может быть разложено на элементарные тензорные операции, что позволяет избежать непараллельных циклов на уровне языка и плохого управления памятью.

Помимо того, что тензоры являются удобными инструментами, они играют важную роль в достижении вычислительной эффективности. Все, кто участвует в разработке операционной глубокой модели, от проектировщиков драйверов, библиотек и моделей до проектировщиков компьютеров и чипов, знают, что данные будут обрабатываться как тензоры. Возникающие ограничения на локальность и блочную декомпозируемость позволяют всем участникам этой цепочки создавать оптимальные конструкции.

Глава 3
Обучение

Как было введено в § 1.1, обучение модели заключается в минимизации функции потерь $\mathcal{L}(w)$, которая отражает производительность предсказателя $f(\cdot;w)$ на обучающем наборе $\mathcal{D}$.

Поскольку модели обычно чрезвычайно сложны, а их производительность напрямую связана с тем, насколько хорошо минимизируется функция потерь, эта минимизация является ключевой задачей, включающей как вычислительные, так и математические трудности.

3.1 Функции потерь

Пример среднеквадратичной ошибки из Уравнения 1.1 является стандартной функцией потерь для предсказания непрерывного значения.

Для моделирования плотности стандартной функцией потерь является правдоподобие данных. Если $f(x;w)$ интерпретировать как нормализованный логарифм вероятности или логарифм плотности, то функция потерь является противоположностью суммы ее значений по обучающим выборкам, что соответствует правдоподобию набора данных.

Перекрестная энтропия

Для классификации обычная стратегия заключается в том, что выход модели представляет собой вектор с одним компонентом $f(x;w)_y$ для каждого класса $y$, интерпретируемым как логарифм ненормализованной вероятности, или логит.

Имея $X$ в качестве входного сигнала и $Y$ в качестве класса для предсказания, мы можем вычислить по $f$ оценку апостериорных вероятностей:

$$\hat{P}(Y = y | X = x) = \frac{\exp f(x;w)_y}{\sum_z \exp f(x;w)_z}$$

Это выражение обычно называется softmax, или, более точно, softargmax, логитов.

Для согласования с этой интерпретацией модель должна быть обучена максимизировать вероятность истинных классов, следовательно, минимизировать перекрестную энтропию, выраженную как:

$$\mathcal{L}_{ce}(w) = -\frac{1}{N} \sum_{n=1}^N \log \hat{P}(Y = y_n | X = x_n)$$

$$ = \frac{1}{N} \sum_{n=1}^N -\log \frac{\exp f(x_n;w)_{y_n}}{\sum_z \exp f(x_n;w)_z} \quad \mathcal{L}_{ce}(f(x_n;w),y_n)$$

Контрастивная функция потерь

В некоторых случаях, даже если предсказываемое значение является непрерывным, обучение принимает форму ограничений на ранжирование. Типичная область, где это происходит, — метрическое обучение, целью которого является изучение меры расстояния между выборками таким образом, чтобы выборка $x_a$ из определенного семантического класса была ближе к любой выборке $x_b$ того же класса, чем к любой выборке $x_c$ из другого класса. Например, $x_a$ и $x_b$ могут быть двумя фотографиями одного человека, а $x_c$ — фотографией кого-то другого.

Стандартный подход для таких случаев заключается в минимизации контрастивной функции потерь, в этом случае, например, суммы по триплетам $(x_a,x_b,x_c)$, таких что $y_a = y_b \neq y_c$,

$$\max(0,1-f(x_a,x_c;w)+f(x_a,x_b;w))$$

Эта величина будет строго положительной, если только $f(x_a,x_c;w) \ge 1+f(x_a,x_b;w)$.

Инжиниринг функции потерь

Обычно функция потерь, минимизируемая во время обучения, не является фактической величиной, которую в конечном итоге нужно оптимизировать, но является прокси, для которого легче найти оптимальные параметры модели. Например, перекрестная энтропия является стандартной функцией потерь для классификации, хотя фактическая мера производительности — это частота ошибок классификации, потому что последняя не имеет информативного градиента, что является ключевым требованием, как мы увидим в § 3.3.

Также возможно добавить к функции потерь слагаемые, зависящие от обучаемых параметров самой модели, чтобы способствовать определенным конфигурациям.

Регуляризация по убыванию веса, например, заключается в добавлении к функции потерь слагаемого, пропорционального сумме квадратов параметров. Это можно интерпретировать как наличие гауссовского байесовского априорного распределения на параметрах, которое способствует меньшим значениям и тем самым уменьшает влияние данных. Это ухудшает производительность на обучающем

наборе, но уменьшает разрыв между производительностью при обучении и производительностью на новых, невиданных данных.

3.2 Авторегрессионные модели

Ключевым классом методов, особенно для работы с дискретными последовательностями в обработке естественного языка и компьютерном зрении, являются авторегрессионные модели.

Правило цепи для вероятностей

Такие модели используют правило цепи из теории вероятностей:

$$P(X_1 = x_1, X_2 = x_2, ..., X_T = x_T) = P(X_1 = x_1) \times P(X_2 = x_2 | X_1 = x_1) \times ... \times P(X_T = x_T | X_1 = x_1, ..., X_{T-1} = x_{T-1})$$

Хотя это разложение действительно для случайной последовательности любого типа, оно особенно эффективно, когда интересующий сигнал представляет собой последовательность токенов из конечного словаря $\{1,...K\}$.

С соглашением, что дополнительный токен $\emptyset$ обозначает «неизвестную» величину, мы можем представить событие $\{X_1 = x_1,...,X_t = x_t\}$ как вектор $(x_1,...,x_t,\emptyset,...,\emptyset)$.

Затем, модель

$$f : \{\emptyset,1,...,K\}^T \to \mathbb{R}^K$$

которая, получив такой вход, вычисляет вектор $l_t$ из $K$ логитов, соответствующих

$$\hat{P}(X_t | X_1 = x_1,...,X_{t-1} = x_{t-1})$$

позволяет выбрать один токен, основываясь на предыдущих.

Правило цепи гарантирует, что, выбирая $T$ токенов $x_t$, по одному за раз, основываясь на ранее выбранных $x_1,...,x_{t-1}$, мы получаем последовательность, которая соответствует совместному распределению. Это авторегрессионная генеративная модель.

Обучение такой модели может быть выполнено путем минимизации суммы по обучающим последовательностям и временным шагам функции потерь кросс-энтропии

$$\mathcal{L}_{ce}(f(x_1,...,x_{t-1},\emptyset,...,\emptyset;w),x_t)$$

что формально эквивалентно максимизации правдоподобия истинных $x_t$.

Значение, которое классически отслеживается, — это не сама кросс-энтропия, а перплексия, которая определяется как экспонента кросс-энтропии. Она соответствует количеству значений равномерного распределения с той же энтропией, что, как правило, более интерпретируемо.

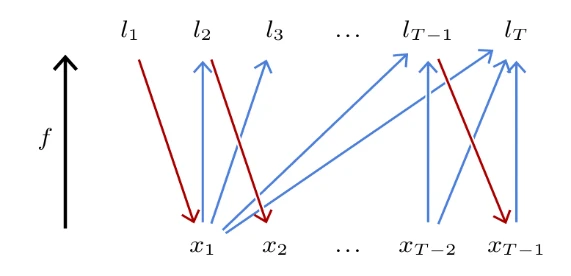
Рисунок 3.1

Причинные модели

Описанная процедура обучения требует разного входного сигнала для каждого $t$, и большая часть вычислений, выполненных для $t < t'$, повторяется для $t'$. Это чрезвычайно неэффективно, поскольку $T$ часто порядка сотен или тысяч.

Стандартная стратегия решения этой проблемы заключается в разработке модели $f$, которая предсказывает все векторы логитов $l_1,...,l_T$ сразу, то есть:

$$f : \{1,...,K\}^T \to \mathbb{R}^{T \times K}$$

но с такой вычислительной структурой, что вычисленные логиты $l_t$ для $x_t$ зависят только от входных значений $x_1,...,x_{t-1}$.

Такая модель называется причинной, поскольку она соответствует, в случае временных рядов, тому, что будущее не влияет на прошлое, как показано на Рисунке 3.1.

Следствием является то, что выход на каждой позиции является тем, который был бы получен, если бы входные данные были доступны только до этой позиции. Во время обучения это позволяет вычислить выход для полной последовательности и максимизировать предсказанные вероятности всех токенов этой последовательности, что снова сводится к минимизации суммы кросс-энтропии для каждого токена.

Обратите внимание, что для простоты мы определили $f$ как работающую с последовательностями фиксированной длины $T$. Однако модели, используемые на практике, такие как трансформеры, которые мы увидим в § 5.3, способны обрабатывать последовательности произвольной длины.

Токенизатор

Важной технической деталью при работе с естественными языками является то, что представление в виде токенов может быть выполнено различными способами, от мельчайшей гранулярности отдельных символов

до целых слов. Преобразование в представление токенов и обратно выполняется отдельным алгоритмом, называемым токенизатором.

Стандартным методом является Byte Pair Encoding (BPE) [Sennrich et al., 2015], который строит токены путем иерархического слияния групп символов, пытаясь получить токены, представляющие фрагменты слов различной длины, но с похожей частотой, распределяя токены как на длинные частые фрагменты, так и на редкие отдельные символы.

3.3 Градиентный спуск

За исключением специфических случаев, таких как линейная регрессия, которую мы видели в § 1.2, оптимальные параметры $w^*$ не имеют замкнутого выражения. В общем случае инструментом выбора для минимизации функции является градиентный спуск. Он начинается с инициализации параметров случайным $w_0$, а затем улучшает эту оценку, итеративно выполняя шаги градиента, каждый из которых состоит в вычислении градиента функции потерь по параметрам и вычитании его доли:

$$w_{n+1} = w_n - \eta \nabla \mathcal{L}|_w(w_n) \quad (3.1)$$

Эта процедура соответствует перемещению текущей оценки немного в направлении, которое локально максимально уменьшает $\mathcal{L}(w)$, как показано на Рисунке 3.2.

Скорость обучения

Гиперпараметр $\eta$ называется скоростью обучения. Это положительное значение, которое регулирует скорость минимизации, и его нужно выбирать тщательно.

Если оно слишком мало, оптимизация будет медленной в лучшем случае и может застрять в локальном минимуме рано. Если оно слишком велико, оптимизация может

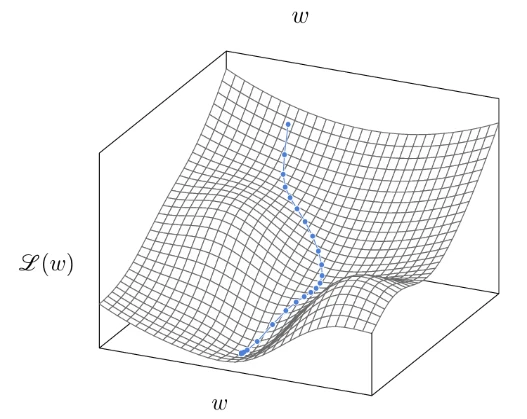
Рисунок 3.2

прыгать вокруг хорошего минимума и никогда не спускаться в него. Как мы увидим в § 3.6, оно может зависеть от номера итерации $n$.

Стохастический градиентный спуск

Все функции потерь, используемые на практике, могут быть выражены как среднее значение функции потерь для небольшой группы выборок или для каждой выборки, например:

$$\mathcal{L}(w) = \frac{1}{N} \sum_{n=1}^N \ell_n(w)$$

где $\ell_n(w) = L(f(x_n;w),y_n)$ для некоторой функции $L$, и тогда градиент равен:

$$\nabla \mathcal{L}|_w(w) = \frac{1}{N} \sum_{n=1}^N \nabla \ell_n|_w(w) \quad (3.2)$$

Получающийся градиентный спуск вычислял бы точную сумму в Уравнении 3.2, что обычно вычислительно тяжело, а затем обновлял бы параметры согласно Уравнению 3.1. Однако при разумных предположениях о взаимозаменяемости, например, если выборки были должным образом перемешаны, любая частичная сумма Уравнения 3.2 является несмещенной оценкой полной суммы, хотя и зашумленной. Таким образом, обновление параметров по частичным суммам соответствует выполнению большего количества шагов градиента

при том же вычислительном бюджете, но с более зашумленными оценками градиента. Из-за избыточности в данных это оказывается гораздо более эффективной стратегией.

Мы видели в § 2.1, что обработка пакета выборок, достаточно малого, чтобы поместиться в память вычислительного устройства, обычно происходит так же быстро, как и обработка одной выборки. Следовательно, стандартный подход заключается в разделении всего набора $\mathcal{D}$ на пакеты и обновлении параметров на основе оценки градиента, вычисленной по каждому пакету. Это называется мини-пакетный стохастический градиентный спуск, или сокращенно стохастический градиентный спуск (SGD).

Важно отметить, что этот процесс чрезвычайно постепенный, и количество мини-пакетов и шагов градиента обычно составляет порядка нескольких миллионов.

Как и во многих алгоритмах, интуиция перестает работать в высоких измерениях, и хотя может показаться, что эта процедура легко застрянет в локальном минимуме, на самом деле, из-за количества параметров, дизайна моделей и стохастичности данных, ее эффективность намного выше, чем можно было бы ожидать.

Было предложено множество вариаций этой стандартной стратегии. Самая популярная —

Adam [Kingma and Ba, 2014], который сохраняет текущие оценки среднего и дисперсии каждого компонента градиента и автоматически нормализует их, избегая проблем масштабирования и различной скорости обучения в разных частях модели.

3.4 Обратное распространение ошибки (Backpropagation)

Использование градиентного спуска требует технического средства для вычисления $\nabla \ell|_w(w)$, где $\ell = L(f(x;w);y)$. Учитывая, что $f$ и $L$ являются композициями стандартных тензорных операций, как и для любого математического выражения, правило цепи из дифференциального исчисления позволяет получить его выражение.

Чтобы сделать нотацию легче, мы не будем указывать точку, в которой вычисляются градиенты, поскольку контекст делает это ясным.

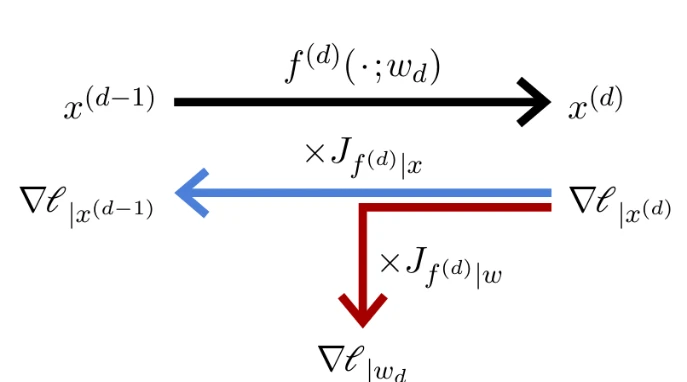
Рисунок 3.3

Прямой и обратный проходы

Рассмотрим простой случай композиции отображений:

$$f = f^{(D)} \circ f^{(D-1)} \circ \cdots \circ f^{(1)}$$

Выход $f(x;w)$ может быть вычислен, начиная с $x^{(0)} = x$ и итеративно применяя:

$$x^{(d)} = f^{(d)}(x^{(d-1)};w_d)$$

с $x^{(D)}$ в качестве конечного значения.

Отдельные скалярные значения этих промежуточных результатов $x^{(d)}$ традиционно называются активациями по аналогии с активациями нейронов; значение $D$ — это глубина модели; отдельные отображения $f^{(d)}$ называются слоями, как мы увидим в § 4.1, а их последовательное вычисление — прямым проходом (см. Рисунок 3.3, верх).

Напротив, градиент $\nabla \ell|_{x^{(d-1)}}$ функции потерь по выходу $x^{(d-1)}$ функции $f^{(d-1)}$ является произведением градиента $\nabla \ell|_{x^{(d)}}$ по выходу $f^{(d)}$, умноженного на якобиан $J_{f^{(d-1)}|x}$ функции $f^{(d-1)}$ по ее переменной $x$. Таким образом, градиенты по выходам всех $f^{(d)}$ могут быть рекурсивно вычислены в обратном порядке, начиная с $\nabla \ell|_{x^{(D)}} = \nabla L|_x$.

И градиент, который нас интересует для обучения, то есть $\nabla \ell|_{w_d}$, является градиентом по выходу $f^{(d)}$, умноженным на якобиан $J_{f^{(d)}|w}$ функции $f^{(d)}$ по параметрам.

Это итеративное вычисление градиентов по промежуточным активациям, объединенное с вычислением градиентов по параметрам слоев, составляет обратный проход (см. Рисунок 3.3, низ). Сочетание этого вычисления с процедурой градиентного спуска называется обратным распространением ошибки (backpropagation).

На практике детали реализации прямого и обратного проходов скрыты от программистов. Фреймворки глубокого обучения способны автоматически строить последовательность операций для вычисления градиентов.

Особо удобным алгоритмом является Autograd [Baydin et al., 2015], который отслеживает тензорные операции и на лету строит комбинацию операторов для градиентов. Благодаря этому, фрагмент императивного программирования, который манипулирует тензорами, может автоматически вычислять градиент любой величины по любой другой.

Использование ресурсов

Что касается вычислительной стоимости, как мы увидим, большая часть вычислений приходится на линейные операции, каждая из которых требует одного матричного произведения для прямого прохода и двух для произведений якобианов для обратного прохода, что делает последний примерно в два раза более затратным, чем первый.

Требования к памяти во время инференса примерно равны требованиям наиболее требовательного отдельного слоя. Однако для обучения обратный проход требует сохранения активаций, вычисленных во время прямого прохода, для вычисления якобианов, что приводит к использованию памяти, которое растет пропорционально глубине модели. Существуют методы для обмена использования памяти на вычисления, либо полагаясь на обратимые слои [Gomez et al., 2017], либо используя контрольные точки (checkpointing), что заключается в хранении активаций только для некоторых слоев и пересчете остальных на лету с частичными прямыми проходами во время обратного прохода [Chen et al., 2016].

Исчезающий градиент

Ключевой исторической проблемой при обучении большой сети является то, что при распространении градиента назад через оператор он может масштабироваться мультипликативным фактором и, следовательно, экспоненциально уменьшаться или увеличиваться при прохождении через множество слоев. Стандартный метод предотвращения его взрыва — отсечение нормы градиента, которое заключается в перемасштабировании градиента для установки его нормы до фиксированного порога, если она превышает его [Pascanu et al., 2013].

Когда градиент экспоненциально уменьшается, это называется исчезающим градиентом, и это может сделать обучение невозможным или, в более мягкой форме, вызвать обновление разных частей модели с разной скоростью, ухудшая их взаимную адаптацию [Glorot and Bengio, 2010].

Как мы увидим в Главе 4, было разработано множество техник для предотвращения этого, что отражает изменение перспективы, которое было критически важным для успеха глубокого обучения: вместо попыток улучшить общие методы оптимизации, усилия сместились на инжиниринг самих моделей, чтобы сделать их оптимизируемыми.

3.5 Ценность глубины

Как указывает термин «глубокое обучение», полезные модели обычно представляют собой длинные последовательности отображений. Обучение их с помощью градиентного спуска приводит к сложной взаимной адаптации отображений, даже если эта процедура является постепенной и локальной.

Мы можем проиллюстрировать это поведение на простом примере модели $\mathbb{R}^2 \to \mathbb{R}^2$, которая объединяет восемь слоев, каждый из которых умножает свой вход на матрицу 2×2 и применяет Tanh по компонентам, с финальным линейным классификатором. Это упрощенная версия стандартного многослойного перцептрона, который мы увидим в § 5.1.

Если мы обучим эту модель с помощью SGD и кросс-энтропии на игрушечной задаче бинарной классификации (Рисунок 3.4, верхний левый), матрицы взаимно адаптируются, чтобы деформировать пространство до тех пор, пока классификация не станет правильной, что подразумевает, что данные стали линейно разделимыми перед финальной аффинной операцией (Рисунок 3.4, нижний правый).

Такой пример дает представление о том, чего может достичь глубокая модель; однако он частично вводит в заблуждение из-за низкой размерности как обрабатываемого сигнала, так и внутренних представлений. Все здесь сохранено в 2D ради

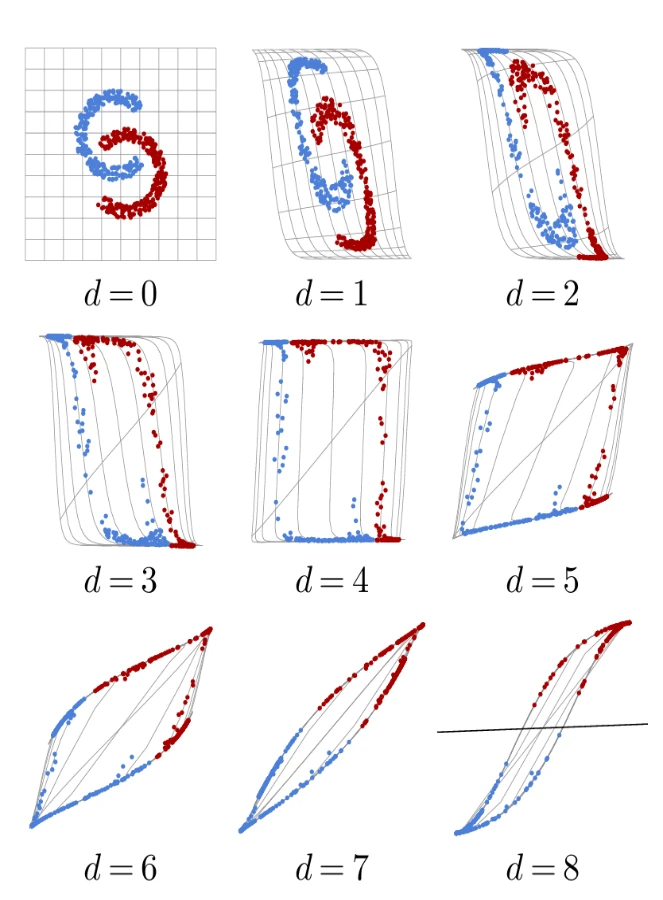
Рисунок 3.4

визуализации, в то время как реальные модели используют представления в высоких измерениях, что, в частности, облегчает оптимизацию, предоставляя множество степеней свободы.

Эмпирические данные, накопленные за двадцать лет, демонстрируют, что современная производительность в различных областях применения требует моделей с десятками слоев, таких как остаточные сети (см. § 5.2) или трансформеры (см. § 5.3).

Теоретические результаты показывают, что для фиксированного вычислительного бюджета или количества параметров увеличение глубины приводит к большей сложности результирующего отображения [Telgarsky, 2016].

3.6 Протоколы обучения

Обучение глубокой сети требует определения протокола, чтобы максимально эффективно использовать вычисления и данные, и чтобы гарантировать хорошую производительность на новых данных.

Как мы видели в § 1.3, производительность на обучающих выборках может вводить в заблуждение, поэтому в простейшей установке требуется как минимум два набора выборок: один — обучающий набор, используемый для оптимизации параметров модели, а другой — тестовый набор, используемый для оценки производительности обученной модели.

Кроме того, обычно требуется адаптация гиперпараметров, в частности, связанных с архитектурой модели, скоростью обучения и членами регуляризации в функции потерь. В этом случае требуется набор валидации, который не пересекается ни с обучающим, ни с тестовым наборами, для оценки наилучшей конфигурации.

Полное обучение обычно разбивается на эпохи, каждая из которых соответствует однократному проходу по всем обучающим примерам. Обычная динамика потерь заключается в том, что потери при обучении уменьшаются до тех пор, пока идет оптимизация, в то время как потери при валидации могут достичь минимума после определенного количества эпох, а затем начать увеличиваться, отражая режим переобучения, как

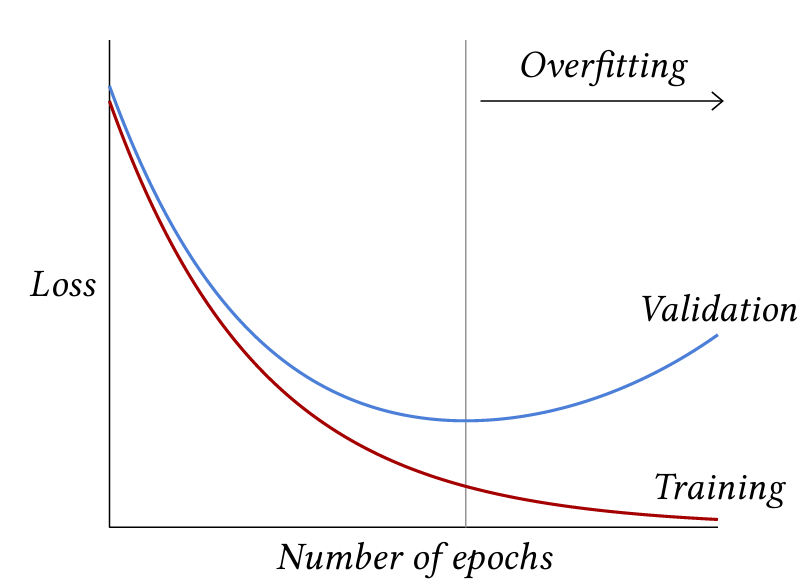
Рисунок 3.5

введено в § 1.3 и проиллюстрировано на Рисунке 3.5.

Парадоксально, но несмотря на то, что большие модели должны страдать от сильного переобучения из-за своей емкости, они обычно продолжают улучшаться по мере обучения. Это может быть связано с тем, что индуктивное смещение модели становится основным драйвером оптимизации, когда производительность близка к идеальной

на обучающем наборе [Belkin et al., 2018].

Важным выбором дизайна является расписание скорости обучения во время обучения, то есть спецификация значения скорости обучения на каждой итерации градиентного спуска. Общая политика заключается в том, что скорость обучения должна быть изначально большой, чтобы избежать застревания оптимизации в плохом локальном минимуме на ранних этапах, и что она должна уменьшаться, чтобы оптимизированные значения параметров не прыгали вокруг и достигали хорошего минимума в узкой долине ландшафта потерь.

Обучение очень больших моделей может занимать месяцы на тысячах мощных GPU и иметь финансовую стоимость в несколько миллионов долларов. В таком масштабе обучение может включать множество ручных вмешательств, основанных, в частности, на динамике эволюции потерь.

Тонкая настройка (Fine-tuning)

Часто выгодно адаптировать уже обученную модель к новой задаче, называемой нисходящей задачей.

Это может быть связано с тем, что объем данных для исходной задачи велик, в то время как для нисходящей задачи он ограничен, и обе задачи имеют достаточно сходств, чтобы статистические структуры, изученные для первой, обеспечивали хорошее индуктивное смещение для второй. Это также может быть сделано для ограничения стоимости обучения путем повторного использования паттернов, закодированных в существующей модели.

Адаптация предварительно обученной модели к конкретной задаче достигается с помощью тонкой настройки (fine-tuning), которая является стандартной процедурой обучения для нисходящей задачи, но которая начинается с предварительно обученной модели вместо использования случайной инициализации.

Это основная стратегия для большинства приложений компьютерного зрения, которые обычно используют модель, предварительно обученную для классификации на ImageNet [Deng et al., 2009] (см. § 6.3 и § 6.4), а также то, как чисто генеративные предварительно обученные большие языковые модели используются в качестве моделей-помощников, способных вести интерактивные диалоги (см. § 7.1).

Мы вернемся к техникам для работы с ограниченными ресурсами при инференсе и для тонкой настройки в Главе 8.

3.7 Преимущества масштаба

Накоплены эмпирические результаты, показывающие, что производительность, например, оцениваемая по потерям на тестовых данных, улучшается с увеличением объема данных в соответствии с замечательными законами масштабирования, при условии соответствующего увеличения размера модели [Kaplan et al., 2020] (см. Рисунок 3.6).

Использование этих законов масштабирования в режиме многомиллиардных выборок возможно отчасти благодаря структуре глубоких моделей, которые могут быть произвольно увеличены, как мы увидим, путем увеличения числа слоев или размерности признаков. Но это также стало возможным благодаря распределенному характеру вычислений, которые они реализуют, и стохастическому градиентному спуску, который требует лишь части данных за раз и может работать с наборами данных, размер которых на порядки превышает объем памяти вычислительного устройства. Это привело к экспоненциальному росту моделей, как показано на Рисунке 3.7.

Типичные модели компьютерного зрения имеют 10–100 миллионов обучаемых параметров и требуют 10¹⁸–10¹⁹ FLOPs для обучения [He et al., 2015; Sevilla et al., 2022]. Языковые модели имеют от 100 миллионов до сотен миллиардов обучаемых параметров и требуют

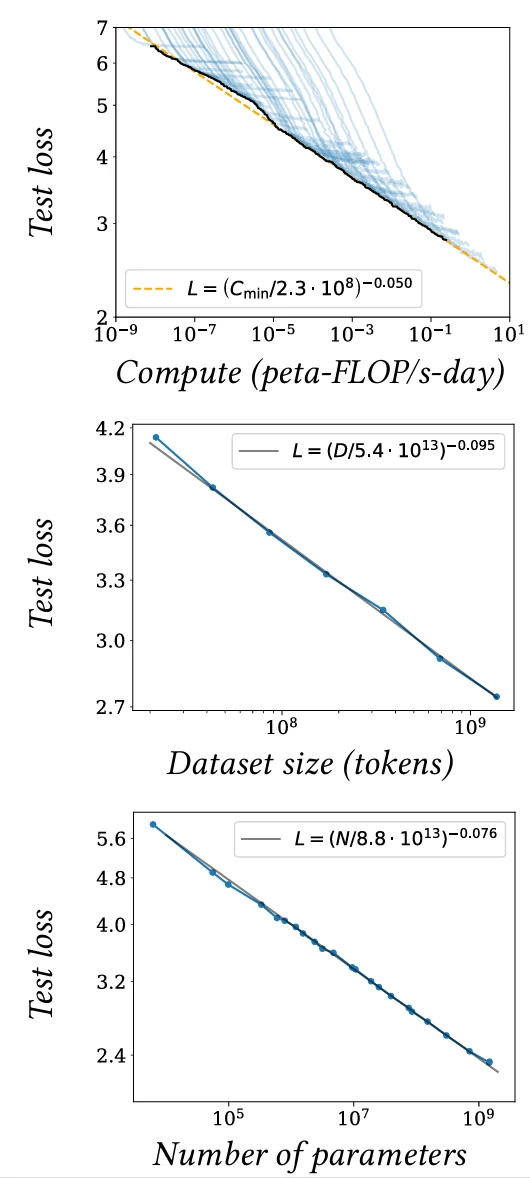
Рисунок 3.6

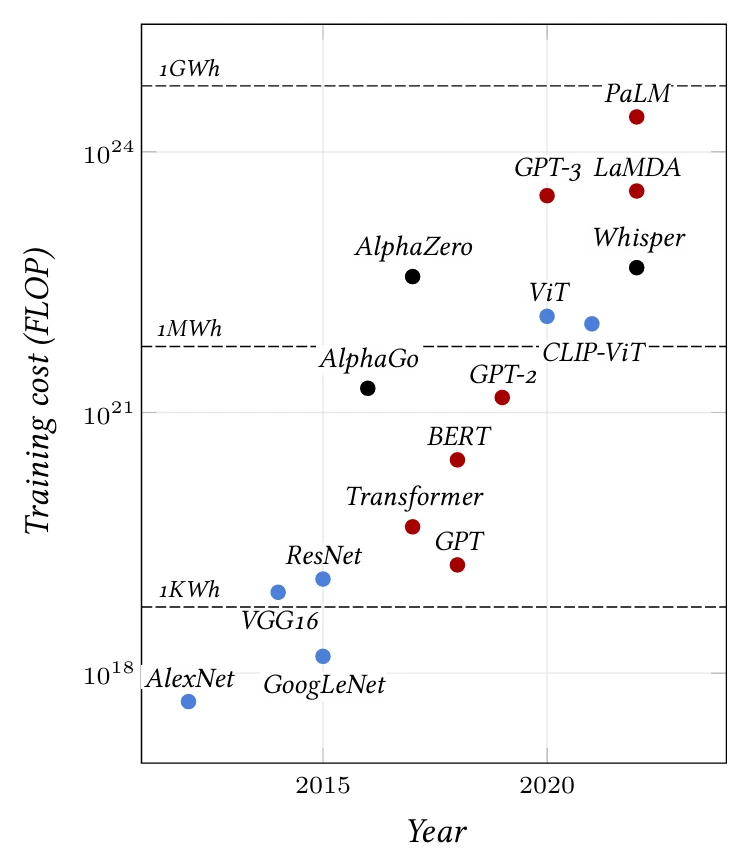
Рисунок 3.7

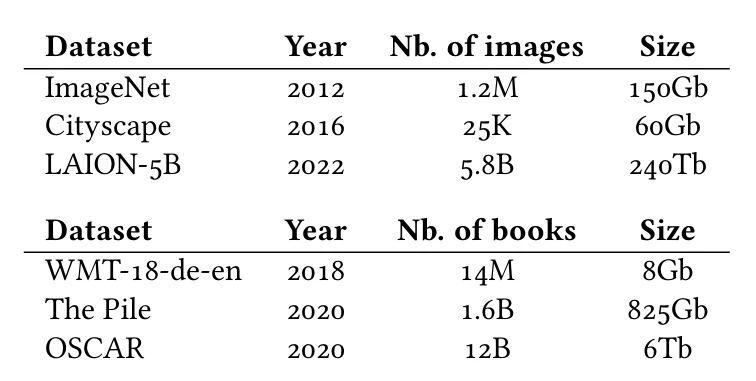
Таблица 3.1

требуют 10²⁰–10²³ FLOPs для обучения [Devlin et al., 2018; Brown et al., 2020; Chowdhery et al., 2022; Sevilla et al., 2022]. Последние модели требуют машин с несколькими высокопроизводительными GPU.

Обучение этих больших моделей невозможно с использованием наборов данных с подробной истинной разметкой, получение которой дорогостояще и возможно только для умеренных размеров. Вместо этого, обучение проводится на наборах данных, автоматически сгенерированных путем объединения данных, доступных в Интернете, с минимальным курированием, если таковое имеется. Эти наборы могут объединять различные модальности, такие как текст и изображения с веб-страниц, или звук и изображения из видео, которые могут быть использованы для крупномасштабного обучения с учителем.

По состоянию на 2024 год самыми мощными моделями являются так называемые большие языковые модели (LLMs), которые мы увидим в § 5.3 и § 7.1, обученные на чрезвычайно больших текстовых наборах данных (см. Таблицу 3.1).

Другие статьи по этой теме:

• 100 Страниц о машинном обучении
• Машинное обучение с помощью Python
• Математика для нейронного обучения