Маленькая книга о глубоком обучении

Часть II Глубокие модели

Глава 4
Компоненты модели

Глубокая модель представляет собой не что иное, как сложное тензорное вычисление, которое в конечном итоге может быть разложено на стандартные математические операции из линейной алгебры и анализа. С годами в этой области была разработана большая коллекция высокоуровневых модулей с четкой семантикой, а также сложные модели, объединяющие эти модули, которые оказались эффективными в конкретных областях применения.

Эмпирические данные и теоретические результаты показывают, что более высокая производительность достигается с более глубокими архитектурами, то есть с длинными композициями отображений. Как мы видели в разделе § 3.4, обучение такой модели является сложной задачей из-за исчезающего градиента, и множество важных технических вкладов смягчили эту проблему.

4.1 Понятие слоя

Мы называем слоями стандартные сложные составные тензорные операции, которые были разработаны и эмпирически определены как общие и эффективные. Они часто включают обучаемые параметры и соответствуют удобному уровню детализации для проектирования и описания больших глубоких моделей. Этот термин унаследован от простых многослойных нейронных сетей, хотя современные модели могут принимать форму сложного графа таких модулей, включающих множество параллельных путей.

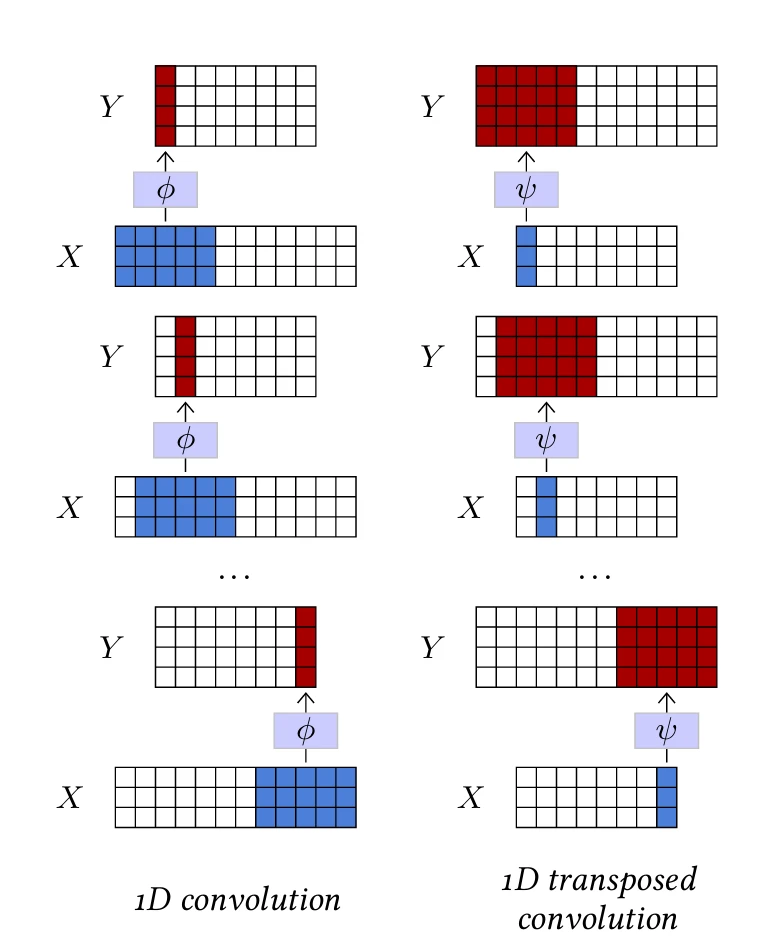
Рисунок 4.1

На следующих страницах я стараюсь придерживаться соглашения об изображении моделей, проиллюстрированного выше:

• операторы/слои изображаются в виде блоков,

• более темный цвет указывает на то, что они содержат обучаемые параметры,

• гиперпараметры с нестандартными значениями

добавляются синим цветом справа от них,

• пунктирная внешняя рамка с мультипликативным фактором указывает на то, что группа слоев повторяется последовательно, каждый со своим набором обучаемых параметров, если таковые имеются, и

• в некоторых случаях размерность их выхода указывается справа, если она отличается от их входа.

Кроме того, слои, имеющие сложную внутреннюю структуру, изображаются с большей высотой.

4.2 Линейные слои

Наиболее важными модулями с точки зрения вычислений и количества параметров являются линейные слои. Они основаны на десятилетиях исследований и разработок в области алгоритмического и чипового проектирования для матричных операций.

Обратите внимание, что термин «линейный» в глубоком обучении обычно не совсем корректно относится к аффинной операции, которая представляет собой сумму линейного выражения и постоянного смещения.

Полносвязные слои

Самый базовый линейный слой — это полносвязный слой, параметризованный обучаемой матрицей весов $W$ размером $D' \times D$ и вектором смещения $b$ размерности $D'$. Он реализует аффинное преобразование, обобщенное на тензоры произвольной формы, где дополнительные размерности интерпретируются как индексы вектора. Формально, при входном тензоре $X$ размерности $D_1 \times \cdots \times D_K \times D$, он вычисляет выходной тензор $Y$ размерности $D_1 \times \cdots \times D_K \times D'$ с

$$\forall d_1,...,d_K, \quad Y[d_1,...,d_K] = W X[d_1,...,d_K]+b$$

Хотя на первый взгляд такая аффинная операция

кажется ограниченной геометрическими преобразованиями, такими как повороты, симметрии и сдвиги, на самом деле она может делать больше. В частности, проекции для уменьшения размерности или фильтрации сигнала, а также, с точки зрения скалярного произведения как меры сходства, матрично-векторное произведение может быть интерпретировано как вычисление оценок соответствия между запросами, закодированными входными векторами, и ключами, закодированными строками матрицы.

Как мы видели в § 3.3, градиентный спуск начинается со случайной инициализации параметров. Если это сделано слишком наивно, как показано в § 3.4, сеть может страдать от взрыва или исчезновения активаций и градиентов [Glorot and Bengio, 2010]. Фреймворки глубокого обучения реализуют методы инициализации, которые, в частности, масштабируют случайные параметры в соответствии с размерностью входа, чтобы сохранить постоянную дисперсию активаций и предотвратить патологическое поведение.

Сверточные слои

Линейный слой может принимать на вход тензор произвольной формы, преобразуя его в вектор, при условии, что у него правильное количество коэффициентов. Однако такой слой плохо приспособлен для работы

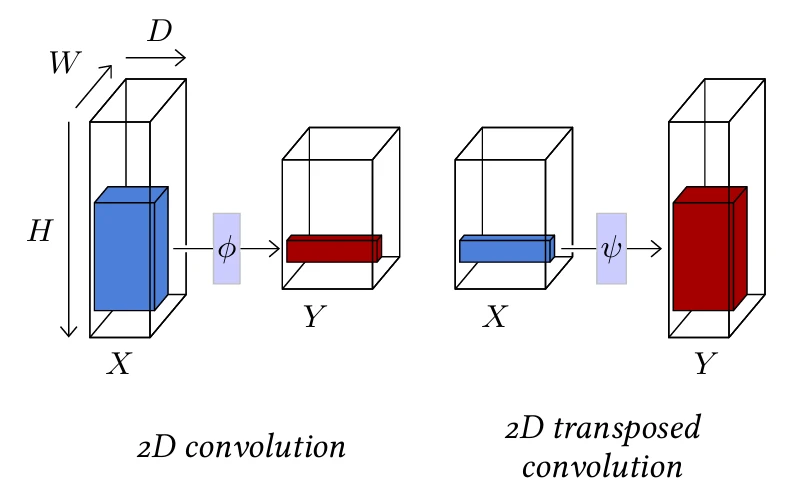
Рисунок 4.2

с большими тензорами, поскольку количество параметров и количество операций пропорциональны произведению размерностей входа и выхода. Например, для обработки RGB-изображения размером 256×256 в качестве входа и вычисления результата того же размера потребуется приблизительно 4×10¹⁰ параметров и умножений.

Помимо этих практических проблем, большинство высокоразмерных сигналов имеют сильную структуру. Например,

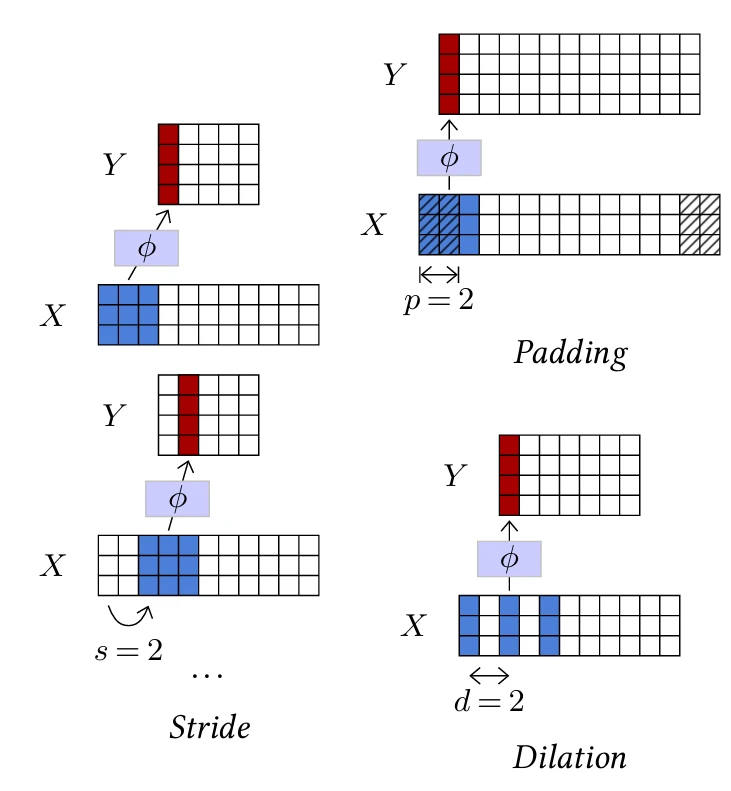
Рисунок 4.3

например, изображения демонстрируют кратковременные корреляции и статистическую стационарность относительно сдвига, масштабирования и определенных симметрий. Это не отражается в индуктивном смещении полносвязного слоя, который полностью игнорирует структуру сигнала.

Для использования этих закономерностей инструментом выбора являются сверточные слои, которые также являются аффинными, но обрабатывают временные ряды или 2D-сигналы локально, с одним и тем же оператором везде.

1D-свертка в основном определяется тремя гиперпараметрами: размером ядра $K$, количеством входных каналов $D$, количеством выходных каналов $D'$, и обучаемыми параметрами $w$ аффинного отображения $\phi(\cdot;w) : \mathbb{R}^{D \times K} \to \mathbb{R}^{D' \times 1}$.

Он может обрабатывать любой тензор $X$ размером $D \times T$ с $T \ge K$, и применяет $\phi(\cdot;w)$ к каждому подтензору размера $D \times K$ из $X$, сохраняя результаты в тензоре $Y$ размера $D' \times (T - K + 1)$, как показано на Рисунке 4.1 (слева).

2D-свертка аналогична, но имеет ядро $K \times L$ и принимает на вход тензор $D \times H \times W$ (см. Рисунок 4.2, слева).

Оба оператора имеют обучаемые параметры $\phi$, которые можно представить как $D'$ фильтров

размера $D \times K$ или $D \times K \times L$ соответственно, и вектор смещения размерности $D'$.

Такой слой эквивариантен к сдвигу, что означает, что если входной сигнал сдвигается, выход аналогично преобразуется. Это свойство приводит к желаемому индуктивному смещению при работе с сигналом, распределение которого инвариантно к сдвигу.

Они также имеют три дополнительных гиперпараметра, проиллюстрированных на Рисунке 4.3:

• Заполнение (padding) указывает, сколько нулевых коэффициентов следует добавить вокруг входного тензора перед его обработкой, в частности, для сохранения размера тензора, когда размер ядра больше единицы. Его значение по умолчанию равно 0.

• Шаг (stride) указывает размер шага, используемого при проходе по входным данным, что позволяет геометрически уменьшить размер выходных данных, используя большие шаги. Его значение по умолчанию равно 1.

• Дилатация (dilation) указывает количество индексов между коэффициентами фильтра локального аффинного оператора. Его значение по умолчанию равно 1, а большие значения соответствуют вставке нулей между коэффициентами, что увеличивает размер фильтра/ядра,

Рисунок 4.4

при этом количество обучаемых параметров остается неизменным.

За исключением количества каналов, выход свертки обычно меньше ее входа. В 1D-случае без заполнения и дилатации, если вход имеет размер $T$, ядро — размер $K$, а шаг — $S$, выход имеет размер $T' = (T - K)/S + 1$.

Учитывая активацию, вычисленную сверточным слоем, или вектор значений для всех каналов в определенном месте, часть входного

сигнала, от которой она зависит, называется ее рецептивным полем (см. Рисунок 4.4). Один из подтензоров $H \times W$, соответствующих одному каналу тензора активаций $D \times H \times W$, называется картой активаций.

Свертки используются для перекомбинации информации, обычно для уменьшения пространственного размера представления в обмен на увеличение количества каналов, что приводит к более богатому локальному представлению. Они могут реализовывать дифференциальные операторы, такие как детекторы границ, или механизмы сопоставления шаблонов. Последовательность таких слоев также может рассматриваться как композиционное и иерархическое представление [Zeiler and Fergus, 2014], или как диффузионный процесс, в котором информация может передаваться на половину размера ядра при прохождении через слой.

Обратная операция — транспонированная свертка, которая также состоит из локализованного аффинного оператора, определяемого аналогичными гиперпараметрами и обучаемыми параметрами, как свертка, но которая, например, в 1D-случае применяет аффинное отображение $\psi(\cdot;w) : \mathbb{R}^{D \times 1} \to \mathbb{R}^{D' \times K}$ к каждому подтензору $D \times 1$ входа и суммирует сдвинутые результирующие тензоры $D' \times K$ для вычисления выхода. Такой оператор увеличивает размер сигнала и может быть интуитивно понят как процесс синтеза

процесс (см. Рисунок 4.1, справа, и Рисунок 4.2, справа).

Последовательность сверточных слоев является обычной архитектурой для отображения сигнала большой размерности, такого как изображение или звуковая выборка, в тензор низкой размерности. Это может быть использовано, например, для получения оценок классов для классификации или сжатого представления. Транспонированные сверточные слои используются в обратном порядке для построения сигнала большой размерности из сжатого представления, либо для оценки того, что сжатое представление содержит достаточно информации для реконструкции сигнала, либо для синтеза, поскольку легче обучить модель плотности на представлении низкой размерности. Мы вернемся к этому в § 5.2.

4.3 Функции активации

Если бы сеть объединяла только линейные компоненты, она сама была бы линейным оператором, поэтому крайне важно иметь нелинейные операции. Они реализуются, в частности, с помощью функций активации, которые представляют собой слои, преобразующие каждый компонент входного тензора индивидуально с помощью отображения, в результате чего получается тензор той же формы.

Существует много разных функций активации, но наиболее часто используемой является Rectified Linear Unit (ReLU) [Glorot et al., 2011], которая устанавливает отрицательные значения равными нулю и оставляет положительные значения без изменений (см. Рисунок 4.5, верхний правый):

$$\text{relu}(x) = \begin{cases} 0 & \text{if } x < 0, \\ x & \text{otherwise}. \end{cases}$$

Учитывая, что основная стратегия обучения глубокого обучения основана на градиенте, может показаться проблематичным иметь отображение, которое недифференцируемо в нуле и постоянно на половине действительной прямой. Однако основное свойство, требуемое градиентным спуском, заключается в том, что градиент в среднем информативен. Инициализация параметров и нормализация данных делают половину активаций положительными

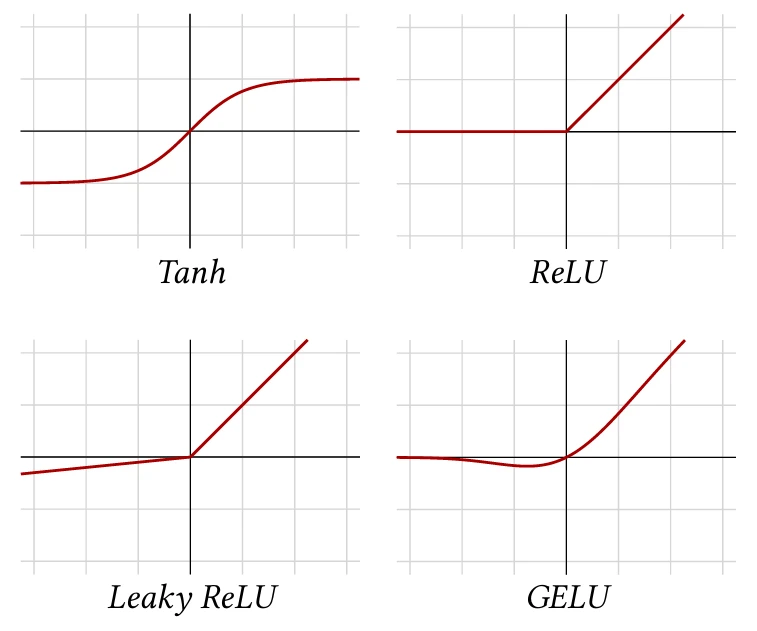
Рисунок 4.5

когда обучение начинается, гарантируя, что это так.

До обобщения ReLU стандартной функцией активации был гиперболический тангенс (Tanh, см. Рисунок 4.5, верхний левый), который экспоненциально быстро насыщается как с отрицательной, так и с положительной стороны, усугубляя проблему исчезающего градиента.

Другие популярные функции активации следуют той же идее сохранения положительных значений неизменными и сжатия отрицательных значений. Leaky ReLU [Maas et al., 2013] применяет небольшой положительный мультипликативный

множитель к отрицательным значениям (см. Рисунок 4.5, нижний левый):

$$\text{leakyrelu}(x) = \begin{cases} ax & \text{if } x < 0, \\ x & \text{otherwise}. \end{cases}$$

А GELU [Hendrycks and Gimpel, 2016] определяется с использованием кумулятивной функции распределения гауссовского распределения, то есть:

$$\text{gelu}(x) = x P(Z \leq x)$$

где $Z \sim \mathcal{N}(0,1)$. Он примерно ведет себя как гладкий ReLU (см. Рисунок 4.5, нижний правый).

Выбор функции активации, в частности среди вариантов ReLU, обычно определяется эмпирической производительностью.

4.4 Пулинг

Классическая стратегия уменьшения размера сигнала — использование операции пулинга, которая объединяет несколько активаций в одну, идеально суммирующую информацию. Наиболее стандартной операцией этого класса является слой максимального пулинга (max pooling), который, аналогично свертке, может работать в 1D и 2D и определяется размером ядра.

В стандартной форме этот слой вычисляет максимальную активацию для каждого канала, по непересекающимся подтензорам пространственного размера, равного размеру ядра. Эти значения сохраняются в результирующем тензоре с тем же количеством каналов, что и у входа, и пространственный размер которого делится на размер ядра. Как и в случае со сверткой, этот оператор имеет три гиперпараметра: заполнение (padding), шаг (stride) и дилатация (dilation), при этом шаг по умолчанию равен размеру ядра. Меньший шаг приводит к большему результирующему тензору, следуя той же формуле, что и для сверток (см. § 4.2).

Операция максимума может быть интуитивно интерпретирована как логическая дизъюнкция, или, когда она следует за серией сверточных слоев, вычисляющих локальные оценки наличия частей, как способ кодирования того, что присутствует хотя бы один экземпляр части. Она теряет точное местоположение, что делает ее

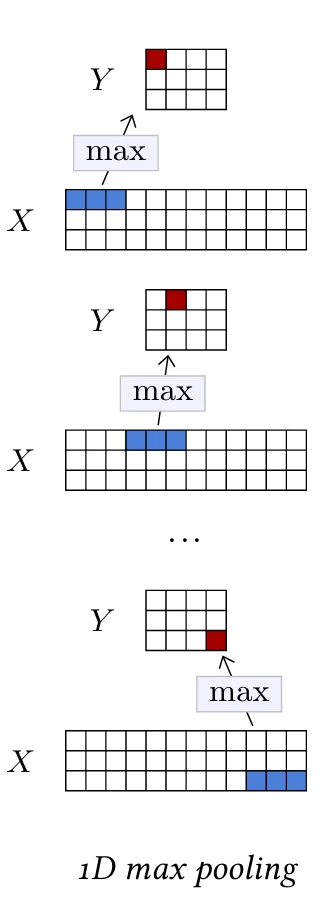
Рисунок 4.6

инвариантной к локальным деформациям.

Стандартной альтернативой является слой усредняющего пулинга (average pooling), который вычисляет среднее значение вместо максимума по подтензорам. Это линейная операция, в то время как максимальный пулинг — нет.

4.5 Dropout

Некоторые слои были разработаны специально для облегчения обучения или улучшения изученных представлений.

Одним из основных вкладов такого рода был дропаут [Srivastava et al., 2014]. Такой слой не имеет обучаемых параметров, но имеет один гиперпараметр $p$ и принимает на вход тензор произвольной формы.

Во время тестирования он обычно отключается, и в этом случае его выход равен его входу. Когда он активен, он с вероятностью $p$ обнуляет каждую активацию входного тензора независимо и перемасштабирует все активации на множитель $\frac{1}{1-p}$, чтобы сохранить ожидаемое значение неизменным (см. Рисунок 4.7).

Мотивация дропаута состоит в том, чтобы способствовать значимым индивидуальным активациям и препятствовать групповым представлениям. Поскольку вероятность того, что группа из $k$ активаций останется неизменной после слоя дропаута, равна $(1-p)^k$, совместные представления становятся ненадежными, что заставляет процедуру обучения избегать их. Это также можно рассматривать как введение шума, которое делает обучение более устойчивым.

При работе с изображениями и 2D-тензорами,

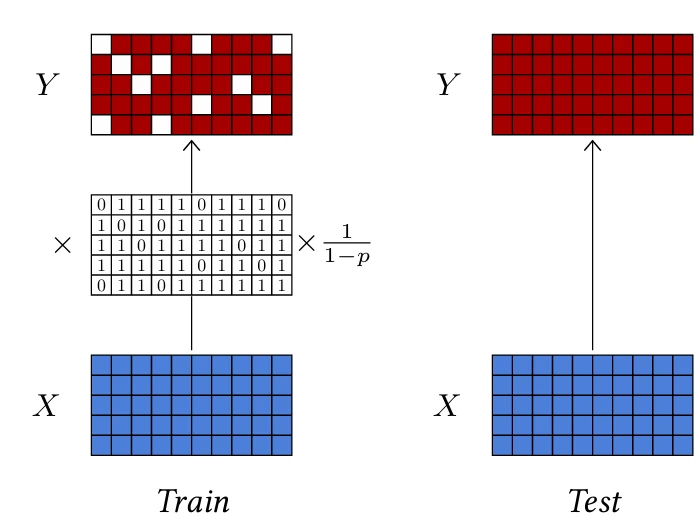
Рисунок 4.7

краткосрочная корреляция сигналов и связанная с этим избыточность нивелируют эффект дропаута, поскольку активации, установленные в ноль, могут быть выведены из их соседей. Следовательно, дропаут для 2D-тензоров обнуляет целые каналы вместо отдельных активаций (см. Рисунок 4.8).

Хотя дропаут обычно используется для улучшения обучения и неактивен во время инференса, его можно использовать в определенных настройках в качестве стратегии рандомизации, например, для эмпирической оценки оценок достоверности [Gal and Ghahramani, 2015].

4.6 Нормализующие слои

Важным классом операторов для облегчения обучения глубоких архитектур являются нормализующие слои, которые принудительно устанавливают эмпирическое среднее и дисперсию групп активаций.

Основным слоем в этом семействе является пакетная нормализация (batch normalization) [Ioffe and Szegedy, 2015], которая является единственным стандартным слоем для обработки пакетов вместо отдельных выборок. Она параметризуется гиперпараметром $D$ и двумя сериями обучаемых скалярных параметров $\beta_1,...,\beta_D$ и $\gamma_1,...,\gamma_D$.

При заданном пакете из $B$ выборок $x_1,...,x_B$ размерности $D$, он сначала вычисляет для каждого из $D$ компонентов эмпирическое среднее $\hat{m}_d$ и дисперсию $\hat{v}_d$ по пакету:

$$\hat{m}_d = \frac{1}{B} \sum_{b=1}^B x_{b,d}$$

$$\hat{v}_d = \frac{1}{B} \sum_{b=1}^B (x_{b,d} - \hat{m}_d)^2$$

из которых он вычисляет для каждого компонента $x_{b,d}$ нормализованное значение $z_{b,d}$ с эмпирическим средним 0 и дисперсией 1, и из него окончательное результирующее значение $y_{b,d}$ со средним $\beta_d$ и стандартным отклонением $\gamma_d$:

Рисунок 4.8

$$\forall b, \quad z_{b,d} = \frac{x_{b,d} - \hat{m}_d}{\sqrt{\hat{v}_d + \epsilon}}$$

$$y_{b,d} = \gamma_d z_{b,d} + \beta_d$$

Поскольку эта нормализация определяется по пакету, она выполняется только во время обучения. Во время тестирования слой преобразует отдельные выборки в соответствии с $\hat{m}_d$ и $\hat{v}_d$, оцененными с помощью скользящего среднего по всему обучающему набору, что сводится к фиксированному аффинному преобразованию для каждого компонента.

Мотивация пакетной нормализации заключалась в том, чтобы избежать того, что изменение масштаба в раннем слое сети во время обучения влияет на все последующие слои, которые затем должны соответствующим образом адаптировать свои обучаемые параметры. Хотя фактический режим действия может быть более сложным, чем эта первоначальная мотивация, этот слой значительно облегчает обучение глубоких моделей.

В случае 2D-тензоров, чтобы следовать принципу сверточных слоев, обрабатывающих все местоположения одинаково, нормализация выполняется для каждого канала по всем 2D-позициям, а $\beta$ и $\gamma$ остаются векторами размерности $D$, так что масштабирование/сдвиг не зависит от 2D-позиции. Следовательно, если обрабатываемый тензор имеет

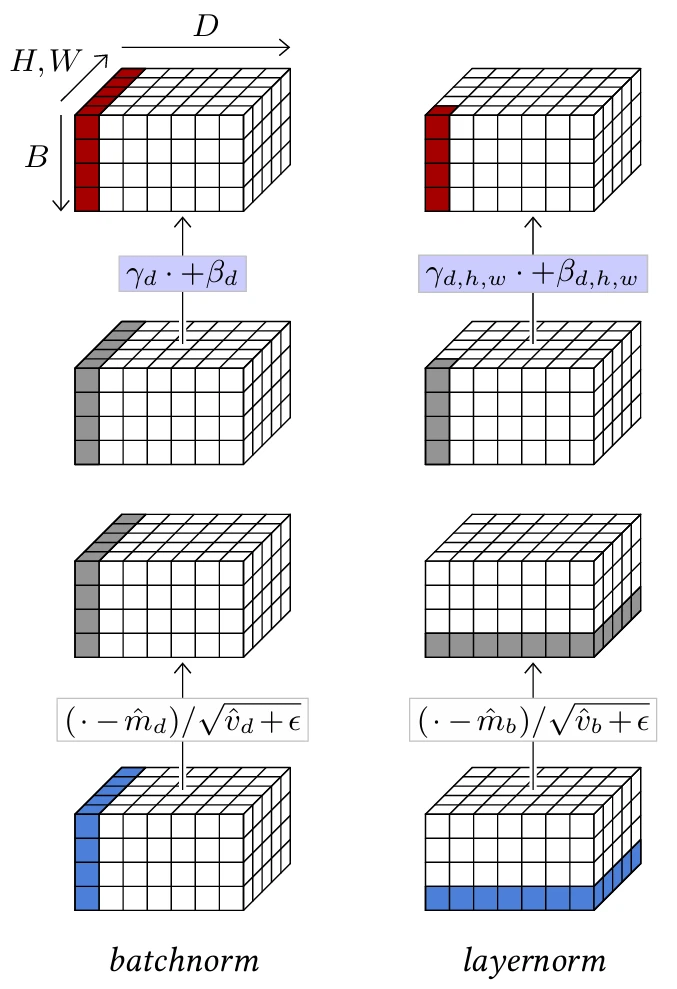
Рисунок 4.9

форму $B \times D \times H \times W$, слой вычисляет $(\hat{m}_d, \hat{v}_d)$ для $d = 1,...,D$ из соответствующего среза $B \times H \times W$, нормализует его соответствующим образом, и, наконец, масштабирует и сдвигает его компоненты с помощью обучаемых параметров $\beta_d$ и $\gamma_d$.

Таким образом, при заданном тензоре $B \times D$ пакетная нормализация нормализует его по $b$ и масштабирует/сдвигает по $d$, что может быть реализовано как поэлементное произведение на $\gamma$ и сумма с $\beta$. При заданном тензоре $B \times D \times H \times W$ она нормализует его по $b,h,w$ и масштабирует/сдвигает по $d$ (см. Рисунок 4.9, слева).

Это может быть обобщено в зависимости от этих размерностей. Например, нормализация слоя (layer normalization) [Ba et al., 2016] вычисляет моменты и нормализует по всем компонентам отдельных выборок, а также масштабирует и сдвигает компоненты индивидуально (см. Рисунок 4.9, справа). Таким образом, при заданном тензоре $B \times D$ он нормализует его по $d$ и масштабирует/сдвигает также по $d$. При заданном тензоре $B \times D \times H \times W$ он нормализует его по $d,h,w$ и масштабирует/сдвигает также по $d,h,w$.

В отличие от пакетной нормализации, поскольку она обрабатывает выборки индивидуально, нормализация слоя ведет себя одинаково как во время обучения, так и во время тестирования.

4.7 Связи пропуска (Skip connections)

Другая техника, которая смягчает проблему исчезающего градиента и позволяет обучать глубокие архитектуры, — это связи пропуска (skip connections) [Long et al., 2014; Ronneberger et al., 2015]. Это не слои сами по себе, а архитектурный дизайн, при котором выходы некоторых слоев передаются в другие слои дальше в модели без промежуточной обработки. Этот неизмененный сигнал может быть конкатенирован или добавлен к входу слоя, в который ветвятся связи (см. Рисунок 4.10). Особым типом связей пропуска являются остаточные связи (residual connections), которые объединяют сигнал с суммой и обычно пропускают всего несколько слоев (см. Рисунок 4.10, справа).

Наиболее желательным свойством этого дизайна является гарантия того, что даже в случае обработки, «убивающей» градиент на определенном этапе, градиент все равно будет распространяться через связи пропуска. Остаточные связи, в частности, позволяют строить глубокие модели с сотнями слоев, а ключевые модели, такие как остаточные сети (residual networks) [He et al., 2015] в компьютерном зрении (см. § 5.2), и трансформеры (Transformers) [Vaswani et al., 2017] в обработке естественного языка (см. § 5.3), полностью состоят из блоков слоев с остаточными связями.

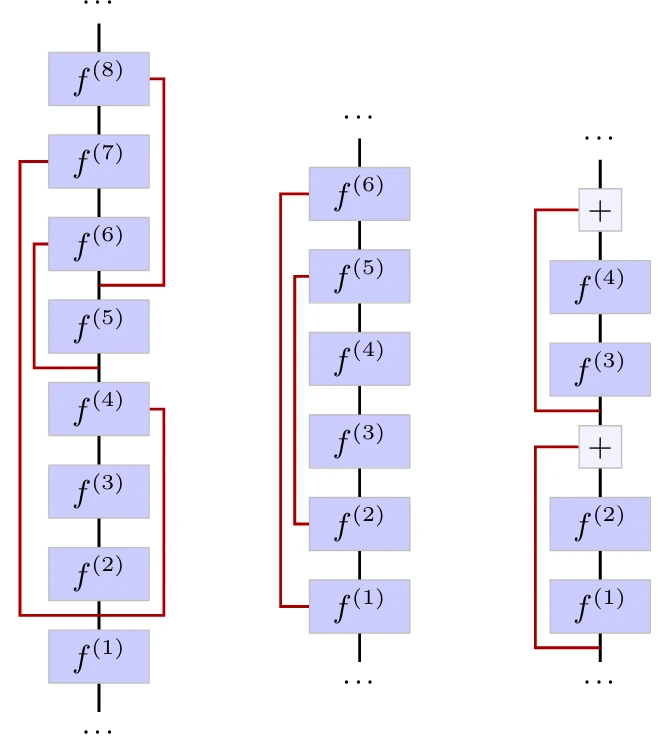
Рисунок 4.10

Их роль также может заключаться в облегчении многомасштабного рассуждения в моделях, которые уменьшают размер сигнала перед его повторным расширением, путем связывания слоев с совместимыми размерами, например, для семантической сегментации (см. § 6.4). В случае остаточных связей они также могут облегчать обучение, упрощая задачу поиска дифференциального улучшения вместо полного обновления.

4.8 Слои внимания (Attention layers)

Во многих приложениях требуется операция, способная объединять локальную информацию в местоположениях, расположенных далеко друг от друга в тензоре. Например, это могут быть удаленные детали для когерентного и реалистичного синтеза изображений, или слова на разных позициях в абзаце для принятия грамматического или семантического решения в обработке естественного языка.

Полносвязные слои не могут обрабатывать сигналы большой размерности, а также сигналы переменного размера, а сверточные слои не способны быстро распространять информацию. Стратегии, агрегирующие результаты сверток, например, путем усреднения по большим пространственным областям, страдают от смешивания множества сигналов в ограниченное количество измерений.

Слои внимания специфически решают эту проблему путем вычисления оценки внимания для каждого компонента результирующего тензора к каждому компоненту входного тензора, без ограничений локальности, и соответствующего усреднения признаков по всему тензору [Vaswani et al., 2017].

Несмотря на то, что они существенно сложнее других слоев, они стали стандартным элементом многих современных моделей. В частности, они являются ключевым строительным блоком трансформеров

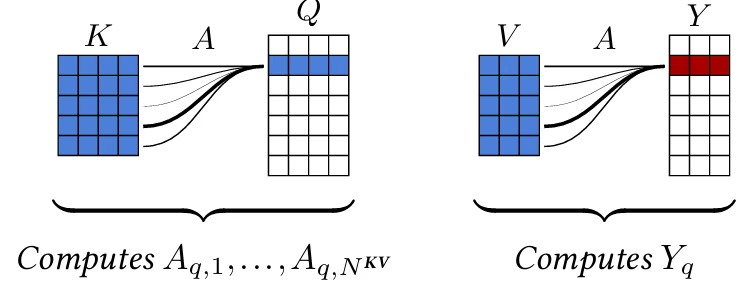
Рисунок 4.11

формеров, доминирующей архитектуры для больших языковых моделей. См. § 5.3 и § 7.1.

Оператор внимания

При заданных

• тензоре $Q$ запросов (queries) размера $N^Q \times D_{QK}$,

• тензоре $K$ ключей (keys) размера $N^{KV} \times D_{QK}$, и

• тензоре $V$ значений (values) размера $N^{KV} \times D_V$,

оператор внимания вычисляет тензор

$$Y = \text{att}(Q,K,V)$$

размерности $N^Q \times D_V$. Для этого он сначала вычисляет для каждого индекса запроса $q$ и каждого индекса ключа $k$ оценку внимания $A_{q,k}$ как softargmax скалярных произведений между запросом $Q_q$ и ключами:

$$A_{q,k} = \frac{\exp \left( \frac{1}{\sqrt{D_{QK}}} Q_q \cdot K_k \right)}{\sum_l \exp \left( \frac{1}{\sqrt{D_{QK}}} Q_q \cdot K_l \right)} \quad (4.1)$$

где масштабирующий множитель $\frac{1}{\sqrt{D_{QK}}}$ сохраняет диапазон значений примерно неизменным даже для больших $D_{QK}$.

Затем для каждого запроса вычисляется извлеченное значение путем усреднения значений в соответствии с оценками внимания (см. Рисунок 4.11):

$$Y_q = \sum_k A_{q,k} V_k \quad (4.2)$$

Таким образом, если запрос $Q_n$ соответствует одному ключу $K_m$ гораздо сильнее, чем всем остальным, соответствующая оценка внимания $A_{n,m}$ будет близка к единице, а извлеченное значение $Y_n$ будет значением $V_m$, связанным с этим ключом. Но если он соответствует нескольким ключам одинаково, то $Y_n$ будет средним значением связанных значений.

Это может быть реализовано как

$$\text{att}(Q,K,V) = \underbrace{\text{softargmax} \left( \frac{QK^T}{\sqrt{D_{QK}}} \right)}_{A} V$$

Этот оператор обычно расширяется двумя способами, как показано на Рисунке 4.12. Во-первых, матрица внимания может быть маскирована путем умножения ее перед нормализацией softargmax на булеву матрицу $M$. Это позволяет, например, сделать оператор причинным, взяв $M$, заполненную единицами ниже диагонали и нулями выше, предотвращая зависимость $Y_q$ от ключей и значений индексов $k$, больших, чем $q$. Во-вторых, матрица внимания обрабатывается слоем дропаута (см. § 4.5) перед умножением на $V$, что обеспечивает обычные преимущества во время обучения.

Поскольку скалярное произведение вычисляется для каждой пары запрос/ключ, вычислительная стоимость оператора внимания квадратична по длине последовательности. Это становится проблематичным, поскольку некоторые приложения этих методов требуют обработки последовательностей длиной в десятки тысяч или более токенов. Были предприняты многочисленные попытки снизить эту стоимость, например, путем объединения плотного внимания к локальному окну с разреженным вниманием дальнего действия [Beltagy et al., 2020] или линеаризации оператора, чтобы воспользоваться ассоциативностью матричного произведения и вычислить произведение ключ-значение перед умножением на запросы [Katharopoulos et al., 2020].

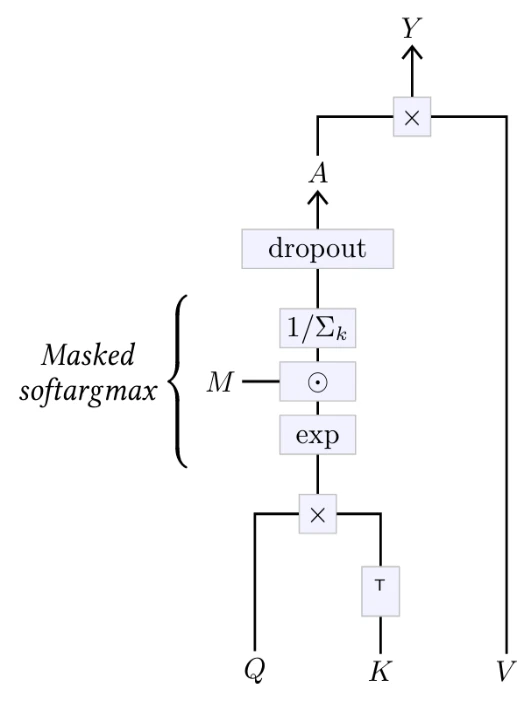
Рисунок 4.12

Многоголовый слой внимания (Multi-head Attention Layer)

Этот оператор внимания без параметров является ключевым элементом многоголового слоя внимания (Multi-Head Attention layer), изображенного на Рисунке 4.13. Структура этого слоя определяется несколькими гиперпараметрами: количеством голов $H$ и формами трех наборов из $H$ обучаемых матриц весов

• $W^Q$ размера $H \times D \times D_{QK}$,

• $W^K$ размера $H \times D \times D_{QK}$, и

• $W^V$ размера $H \times D \times D_V$,

для вычисления соответственно запросов, ключей и значений из входа, и финальной матрицы весов $W^O$ размера $HD_V \times D$ для агрегирования результатов каждой головы.

Он принимает на вход три последовательности

• $X^Q$ размера $N^Q \times D$,

• $X^K$ размера $N^{KV} \times D$, и

• $X^V$ размера $N^{KV} \times D$,

из которых он вычисляет, для $h = 1,...,H$,

$$Y_h = \text{att}(X^Q W^Q_h, X^K W^K_h, X^V W^V_h)$$

Эти последовательности $Y_1,...,Y_H$ конкатенируются по размерности признаков, и каждый отдельный элемент результирующей последовательности умножается

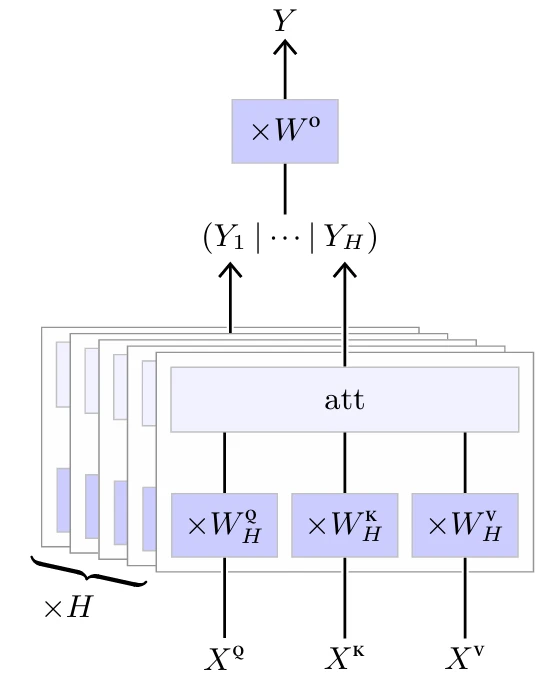
Рисунок 4.13

на $W^O$ для получения окончательного результата:

$$Y = (Y_1 | \cdots | Y_H) W^O$$

Как мы увидим в § 5.3 и на Рисунке 5.6, этот слой используется для построения двух подструктур модели: блоков самовнимания (self-attention blocks), в которых три входные последовательности $X^Q$, $X^K$ и $X^V$ одинаковы, и блоков перекрестного внимания (cross-attention blocks), где $X^K$ и $X^V$ одинаковы.

Примечательно, что оператор внимания, и, следовательно, многоголовый слой внимания при отсутствии маскирования, инвариантен к перестановке ключей и значений, и эквивариантен к перестановке запросов, поскольку он аналогично переставит результирующий тензор.

4.9 Встраивание токенов (Token embedding)

Во многих ситуациях нам необходимо преобразовать дискретные токены в векторы. Это может быть сделано с помощью слоя встраивания (embedding layer), который представляет собой таблицу поиска, непосредственно отображающую целые числа в векторы.

Такой слой определяется двумя гиперпараметрами: числом $N$ возможных значений токенов и размерностью $D$ выходных векторов, а также одной обучаемой матрицей весов $N \times D$, обозначаемой $M$.

При заданном входном целочисленном тензоре $X$ размерности $D_1 \times \cdots \times D_K$ со значениями в $\{0,...,N-1\}$, такой слой возвращает вещественнозначный тензор $Y$ размерности $D_1 \times \cdots \times D_K \times D$ с

$$\forall d_1,...,d_K, \quad Y[d_1,...,d_K] = M[X[d_1,...,d_K]]$$

4.10 Позиционное кодирование (Positional encoding)

В то время как обработка полносвязного слоя специфична как для позиций признаков во входном тензоре, так и для позиций результирующих активаций в выходном тензоре, сверточные слои и многоголовые слои внимания нечувствительны к абсолютной позиции в тензоре. Это является ключом к их сильной инвариантности и индуктивному смещению, что полезно при работе со стационарным сигналом.

Однако это может быть проблемой в определенных ситуациях, когда для правильной обработки необходимо получить доступ к абсолютной позиции. Это относится, например, к синтезу изображений, где статистика сцены не является полностью стационарной, или к обработке естественного языка, где относительные позиции слов сильно влияют на смысл предложения.

Стандартный способ решения этой проблемы — добавление или конкатенация к представлению признаков, на каждой позиции, позиционного кодирования, которое представляет собой вектор признаков, зависящий от позиции в тензоре. Это позиционное кодирование может быть изучено как другие параметры слоя или определено аналитически.

Например, в оригинальной модели Transformer [Vaswani et al., 2017] для серии векторов размерности $D$ добавляется кодирование индекса последовательности в виде серии синусов и косинусов на различных частотах:

$$\text{pos-enc}[t,d] = \begin{cases} \sin \left( \frac{t}{T^{d/D}} \right) & \text{if } d \in 2\mathbb{N} \\ \cos \left( \frac{t}{T^{(d-1)/D}} \right) & \text{otherwise}. \end{cases}$$

с $T = 10^4$.

Глава 5
Архитектуры

Область глубокого обучения развивалась на протяжении многих лет, и для каждой области применения были разработаны различные глубокие архитектуры, демонстрирующие хорошие компромиссы по множеству критериев интереса: например, простота обучения, точность предсказания, занимаемая память, вычислительная стоимость, масштабируемость.

5.1 Многослойные перцептроны (Multi-Layer Perceptrons)

Простейшей глубокой архитектурой является Многослойный перцептрон (MLP), который представляет собой последовательность полносвязных слоев, разделенных функциями активации. Пример можно увидеть на Рисунке 5.1. По историческим причинам в такой модели количество скрытых слоев относится к количеству линейных слоев, за исключением последнего.

Ключевым теоретическим результатом является теорема универсальной аппроксимации [Cybenko, 1989], которая утверждает, что если функция активации $\sigma$ непрерывна

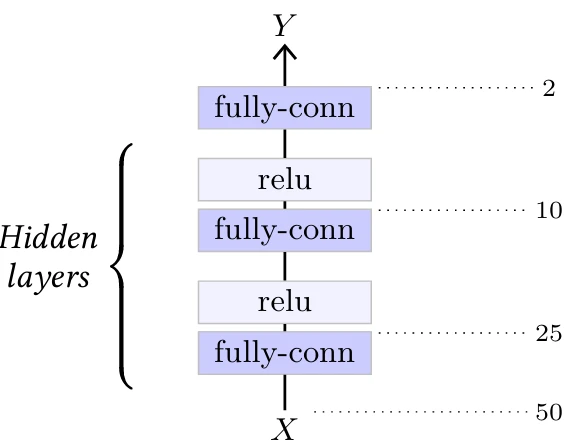
Рисунок 5.1

и не является полиномиальной, любая непрерывная функция $f$ может быть сколь угодно хорошо равномерно аппроксимирована на компактной области, которая ограничена и содержит свою границу, моделью вида $l_2 \circ \sigma \circ l_1$, где $l_1$ и $l_2$ являются аффинными. Такая модель представляет собой MLP с одним скрытым слоем, и этот результат подразумевает, что она может аппроксимировать все, что имеет практическую ценность. Однако эта аппроксимация верна, если размерность выхода первого линейного слоя может быть сколь угодно большой.

Несмотря на свою простоту, MLP остаются важным инструментом, когда размерность обрабатываемого сигнала не слишком велика.

5.2 Сверточные сети (Convolutional networks)

Стандартной архитектурой для обработки изображений является сверточная сеть, или convnet, которая объединяет множество сверточных слоев, либо для уменьшения размера сигнала перед его обработкой полносвязными слоями, либо для вывода 2D-сигнала также большого размера.

LeNet-подобные

Оригинальная модель LeNet для классификации изображений [LeCun et al., 1998] объединяет последовательность 2D-сверточных слоев и слоев максимального пулинга, которые играют роль экстрактора признаков, с последовательностью полносвязных слоев, которые действуют как MLP и выполняют саму классификацию (см. Рисунок 5.2).

Эта архитектура стала образцом для многих моделей, которые имеют похожую структуру и просто крупнее, таких как AlexNet [Krizhevsky et al., 2012] или семейство VGG [Simonyan and Zisserman, 2014].

Остаточные сети (Residual networks)

Стандартные сверточные нейронные сети, следующие архитектуре семейства LeNet, нелегко расширяются до глубоких архитектур и страдают

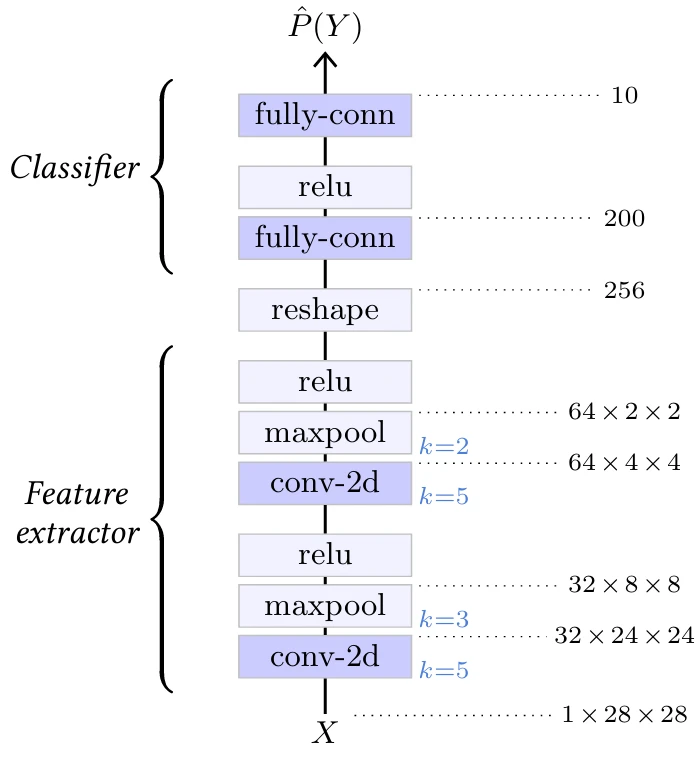
Рисунок 5.2

от проблемы исчезающего градиента. Остаточные сети, или ResNets, предложенные He et al. [2015], явно решают проблему исчезающего градиента с помощью остаточных связей (см. § 4.7), которые позволяют использовать сотни слоев. Они стали стандартными архитектурами для приложений компьютерного зрения и существуют в различных версиях в зависимости от количества слоев. Мы подробно рассмотрим архитектуру ResNet-50 для классификации.

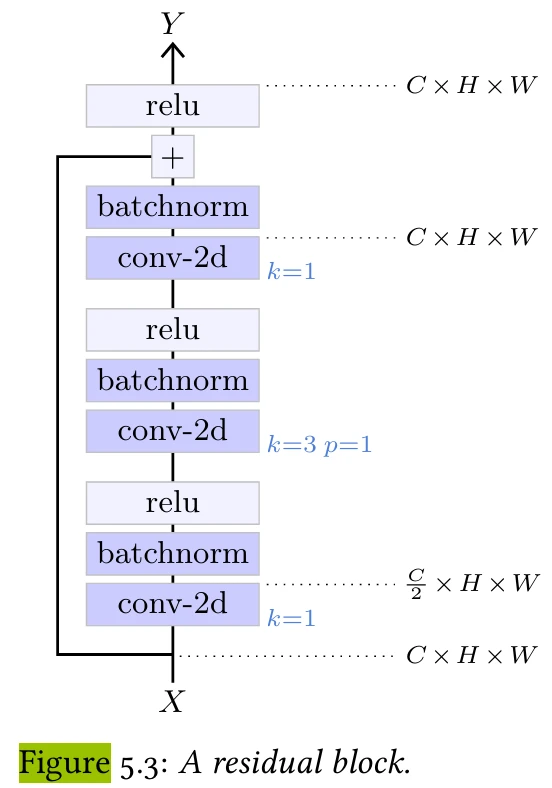
Рисунок 5.3

от проблемы исчезающего градиента. Этот остаточный блок смягчает эту проблему, сначала уменьшая количество каналов с помощью свертки 1×1, затем пространственно работая со сверткой 3×3 на этом уменьшенном количестве каналов, а затем увеличивая количество каналов, снова с помощью свертки 1×1.

Сеть уменьшает размерность сигнала, чтобы в конечном итоге вычислить логиты для классификации. Это достигается благодаря архитектуре, состоящей из нескольких секций, каждая из которых начинается с остаточного блока уменьшения масштаба (downscaling residual block), который уменьшает высоту и ширину сигнала вдвое и удваивает количество каналов, за которым следует серия остаточных блоков. Такой остаточный блок уменьшения масштаба имеет структуру, аналогичную стандартному остаточному блоку, за исключением того, что он требует остаточной связи, которая изменяет форму тензора. Это достигается с помощью свертки 1×1 с шагом два (см. Рисунок 5.4).

Общая структура ResNet-50 представлена на Рисунке 5.5. Она начинается со сверточного слоя 7×7, который преобразует трехканальное входное изображение в 64-канальное изображение половинного размера, за которым следуют четыре секции остаточных блоков. Удивительно,

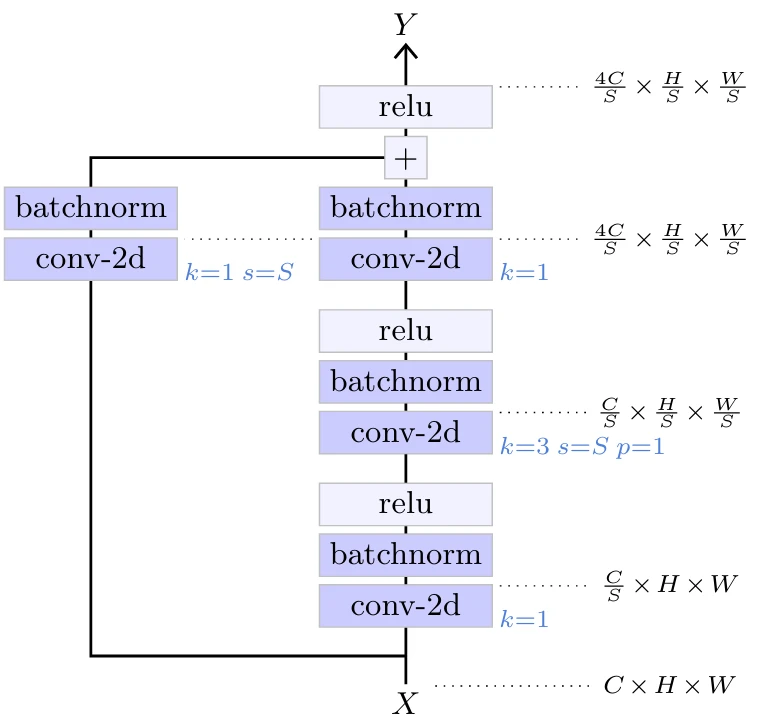
Рисунок 5.4

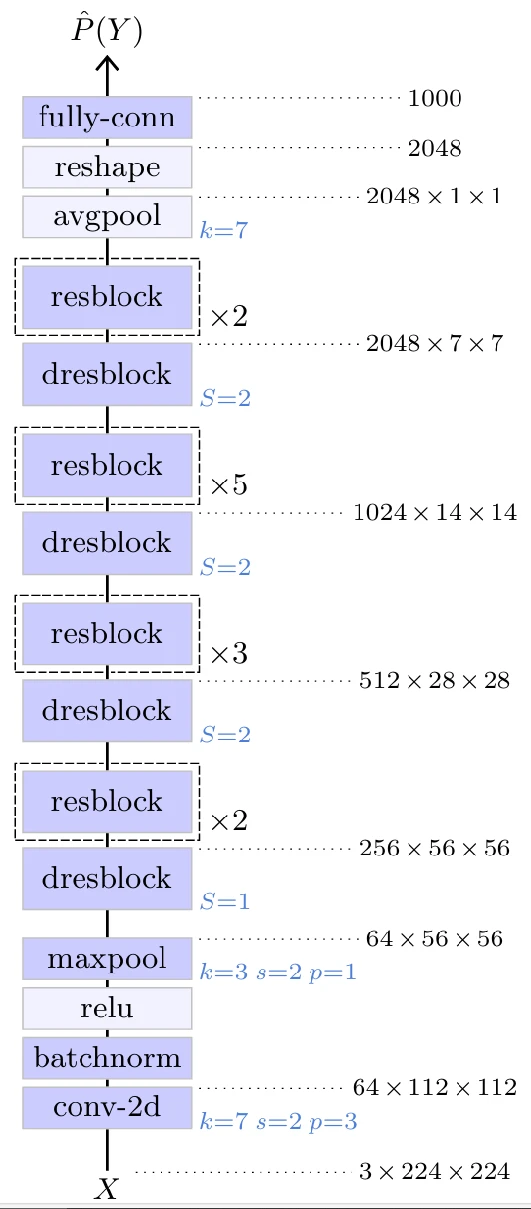
Рисунок 5.5

удивительно, в первой секции нет уменьшения масштаба, только увеличение количества каналов в 4 раза. Выход последнего остаточного блока имеет размер 2048×7×7, который преобразуется в вектор размерности 2048 с помощью усредняющего пулинга с размером ядра 7×7, а затем обрабатывается полносвязным слоем для получения окончательных логитов, здесь для 1000 классов.

5.3 Модели внимания (Attention models)

Как указано в § 4.8, многие приложения, особенно из области обработки естественного языка, значительно выигрывают от моделей, включающих механизмы внимания. Архитектурой выбора для таких задач, которая сыграла важную роль в последних достижениях в глубоком обучении, является Transformer, предложенный Vaswani et al. [2017].

Трансформер

Оригинальный Transformer, изображенный на Рисунке 5.7, был разработан для перевода последовательность-в-последовательность. Он объединяет кодировщик, который обрабатывает входную последовательность для получения уточненного представления, и авторегрессионный декодер, который генерирует каждый токен результирующей последовательности, учитывая представление входной последовательности от кодировщика и уже сгенерированные выходные токены.

Как и остаточные сверточные сети из § 5.2, как кодировщик, так и декодер Transformer представляют собой последовательности составных блоков, построенных с использованием остаточных связей.

• Блок прямого распространения (feed-forward block), изображенный в верхней части Рисунка 5.6, представляет собой MLP с одним скрытым слоем, перед которым стоит нормализация слоя. Он может обновлять представления на каждой позиции отдельно.

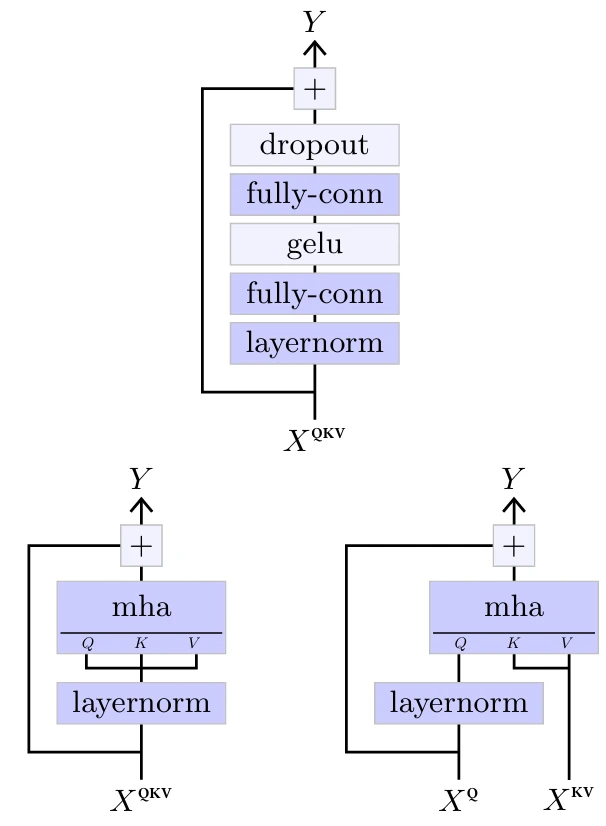
Рисунок 5.6

• Блок самовнимания (self-attention block), изображенный в нижней левой части Рисунка 5.6, представляет собой многоголовый слой внимания (Multi-Head Attention layer) (см. § 4.8), который объединяет информацию глобально, позволяя любой позиции собирать информацию из любых других позиций, перед ним стоит нормализация слоя. Этот блок может быть сделан причинным, используя адекватную маску в слое внимания, как описано в § 4.8

• Блок перекрестного внимания (cross-attention block), изображенный в нижней правой части Рисунка 5.6, аналогичен, за исключением того, что он принимает на вход две последовательности: одну для вычисления запросов и одну для вычисления ключей и значений.

Кодировщик Transformer (см. Рисунок 5.7, снизу) перекодирует входную последовательность дискретных токенов $X_1,...X_T$ с помощью слоя встраивания (см. § 4.9) и добавляет позиционное кодирование (см. § 4.10), прежде чем обработать ее несколькими блоками самовнимания для получения уточненного представления $Z_1,...,Z_T$.

Декодер (см. Рисунок 5.7, сверху) принимает на вход последовательность $Y_1,...,Y_{S-1}$ результирующих токенов, сгенерированных к данному моменту, аналогично перекодирует их с помощью слоя встраивания, добавляет позиционное кодирование и обрабатывает ее чередующимися блоками причинного самовнимания и блоками перекрестного внимания для

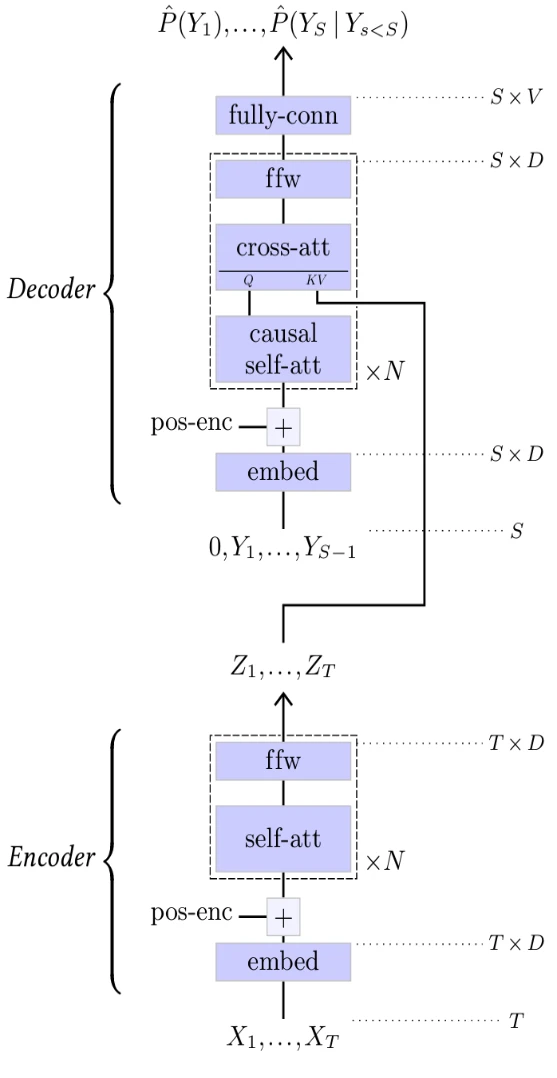
Рисунок 5.7

вычисления логитов, предсказывающих следующие токены. Эти блоки перекрестного внимания вычисляют свои ключи и значения из результирующего представления кодировщика $Z_1,...,Z_T$, что позволяет результирующей последовательности быть функцией исходной последовательности $X_1,...,X_T$.

Как мы видели в § 3.2, причинность гарантирует, что такая модель может быть обучена путем минимизации кросс-энтропии, суммированной по всей последовательности.

Генеративный предварительно обученный трансформер (Generative Pre-trained Transformer)

Генеративный предварительно обученный трансформер (GPT) [Radford et al., 2018, 2019], изображенный на Рисунке 5.8,

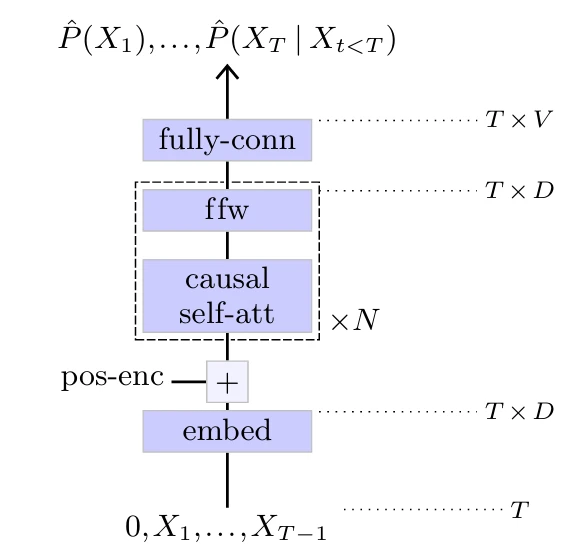
Рисунок 5.8

является чисто авторегрессионной моделью, которая состоит из последовательности блоков причинного самовнимания, следовательно, причинной версии оригинального кодировщика Transformer.

Этот класс моделей чрезвычайно хорошо масштабируется, достигая сотен миллиардов обучаемых параметров [Brown et al., 2020]. Мы вернемся к их использованию для генерации текста в § 7.1.

Визуальный трансформер (Vision Transformer)

Трансформеры были использованы для классификации изображений с моделью Vision Transformer (ViT) [Dosovitskiy et al., 2020] (см. Рисунок 5.9).

Он разбивает трехканальное входное изображение на $M$ патчей разрешением $P \times P$, которые затем выравниваются для создания последовательности векторов $X_1,...,X_M$ формы $M \times 3P^2$. Эта последовательность умножается на обучаемую матрицу $W^E$ формы $3P^2 \times D$, чтобы отобразить ее в последовательность $M \times D$, к которой конкатенируется один обучаемый вектор $E_0$. Получающаяся последовательность $(M+1) \times D$ векторов $E_0,...,E_M$ затем обрабатывается множеством блоков самовнимания. См. § 5.3 и Рисунок 5.6.

Первый элемент $Z_0$ в результирующей последовательности, который соответствует $E_0$ и не связан ни с какой частью изображения, в конечном итоге обрабатывается

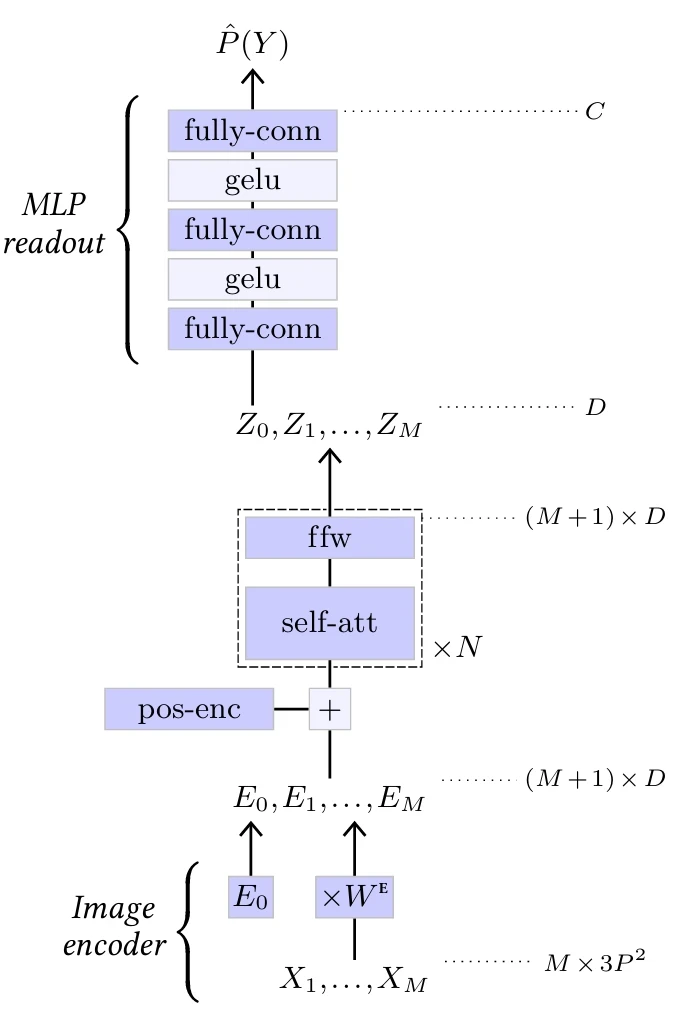
Рисунок 5.9

двухслойным MLP для получения окончательных $C$ логитов. Такой токен, добавленный для считывания классификации, был введен Devlin et al. [2018] в модели BERT и называется CLS-токеном.

Другие статьи по этой теме:

• 100 Страниц о машинном обучении
• Машинное обучение с помощью Python
• Математика для нейронного обучения