Часть III Приложения
Глава 6
Предсказание
Первая категория приложений, таких как распознавание лиц, анализ настроений, обнаружение объектов или распознавание речи, требует предсказания неизвестного значения по доступному сигналу.
6.1 Удаление шума с изображений (Image denoising)
Прямое применение глубоких моделей в обработке изображений заключается в восстановлении от деградации путем использования избыточности в статистической структуре изображений. Лепестки подсолнуха на изображении в оттенках серого могут быть раскрашены с высокой уверенностью, а текстура геометрической формы, такой как стол на слабоосвещенной, зернистой фотографии, может быть скорректирована путем усреднения ее по большой области, которая, вероятно, однородна.
Шумоподавляющий автокодировщик (denoising autoencoder) — это модель, которая принимает деградированный сигнал $\tilde{X}$ в качестве входа и вычисляет оценку исходного сигнала $X$. Для изображений это сверточная сеть, которая может включать связи пропуска, в частности, для объединения представлений с одинаковым разрешением, полученных на ранних и поздних этапах модели, а также слои внимания для облегчения учета элементов, находящихся далеко друг от друга.
Такая модель обучается путем сбора большого количества чистых образцов, связанных с их деградированными входами. Последние могут быть получены в условиях деградации, таких как низкое освещение или неадекватный фокус, или сгенерированы алгоритмически, например, путем преобразования чистого образца в оттенки серого, уменьшения его размера или агрессивного сжатия
методом сжатия с потерями.
Стандартная процедура обучения шумоподавляющих автокодировщиков использует функцию потерь MSE, суммированную по всем пикселям, и в этом случае модель стремится вычислить наилучшее среднее чистое изображение, учитывая деградированное, то есть $\mathbb{E}[X | \tilde{X}]$. Эта величина может быть проблематичной, когда $X$ не полностью определяется $\tilde{X}$, и в этом случае некоторые части сгенерированного сигнала могут быть нереалистичным, размытым средним.
6.2 Классификация изображений (Image classification)
Классификация изображений — это простейшая стратегия извлечения семантики из изображения, которая заключается в предсказании класса из конечного, предопределенного числа классов по заданному входному изображению.
Стандартными моделями для этой задачи являются сверточные сети, такие как ResNets (см. § 5.2), и модели на основе внимания, такие как ViT (см. § 5.3). Эти модели генерируют вектор логитов с количеством размерностей, равным количеству классов.
Процедура обучения просто минимизирует функцию потерь кросс-энтропии (см. § 3.1). Обычно производительность может быть улучшена с помощью аугментации данных, которая заключается в модификации обучающих выборок с помощью разработанных вручную случайных преобразований, не изменяющих семантическое содержание изображения, таких как обрезка, масштабирование, отражение или изменение цвета.
6.3 Обнаружение объектов (Object detection)
Более сложная задача для понимания изображений — обнаружение объектов (object detection), целью которой является предсказание классов и позиций интересующих объектов по входному изображению.
Позиция объекта формализуется четырьмя координатами $(x_1,y_1,x_2,y_2)$ прямоугольного ограничивающего прямоугольника, а истинной разметкой, связанной с каждым обучающим изображением, является список таких ограничивающих прямоугольников, каждый из которых помечен классом содержащегося в нем объекта.
Стандартный подход к решению этой задачи, например, с помощью Single Shot Detector (SSD) [Liu et al., 2015], заключается в использовании сверточной нейронной сети, которая создает последовательность представлений изображений $Z_s$ размера $D_s \times H_s \times W_s$, $s = 1,...,S$, с уменьшающимся пространственным разрешением $H_s \times W_s$ вплоть до $1 \times 1$ для $s = S$ (см. Рисунок 6.1). Каждый из этих тензоров полностью покрывает входное изображение, поэтому индексы $h,w$ соответствуют разбиению решетки изображения на правильные квадраты, которые становятся крупнее при увеличении $s$.
Как видно из § 4.2 и показано на Рисунке 4.4, благодаря последовательности сверточных слоев, вектор признаков $(Z_s[0,h,w],...,Z_s[D_s-1,h,w])$ является дескриптором области изображения, называемой ее
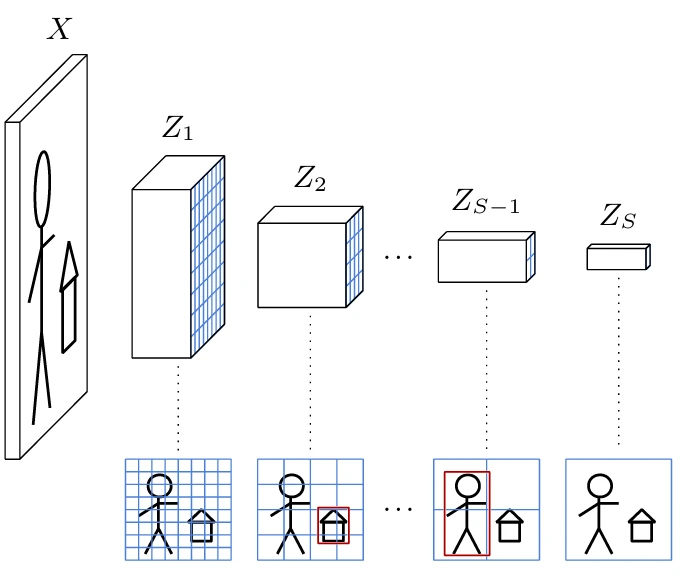
Рисунок 6.1
рецептивным полем, которое больше этого квадрата, но центрировано на нем. Это приводит к недвусмысленному сопоставлению любого ограничивающего прямоугольника $(x_1,x_2,y_1,y_2)$ с $s,h,w$, определяемому соответственно по $\max(x_2-x_1, y_2-y_1)$, $\frac{y_1+y_2}{2}$ и $\frac{x_1+x_2}{2}$.
Обнаружение достигается добавлением $S$ сверточных слоев, каждый из которых обрабатывает $Z_s$ и вычисляет для каждого тензорного индекса $h,w$ координаты ограничивающего прямоугольника и связанные логиты. Если существует $C$ классов объектов, то имеется $C+1$ логит, дополнительный обозначает «нет объекта». Следовательно, каждый дополнительный сверточный слой имеет $4+C+1$ выходных каналов. Алгоритм SSD, в частности, генерирует несколько ограничивающих прямоугольников для каждого $s,h,w$, каждый из которых соответствует жестко заданному диапазону соотношений сторон.
Наборы данных для обучения обнаружения объектов дорогостоящи в создании, поскольку разметка с ограничивающими прямоугольниками требует медленного вмешательства человека. Для смягчения этой проблемы стандартный подход заключается в тонкой настройке сверточной модели, предварительно обученной на большом наборе данных для классификации, таком как VGG-16 для исходного SSD, и замене ее финальных полносвязных слоев дополнительными сверточными. Удивительно, но модели, обученные только для классификации, изучают представления признаков, которые могут быть перепрофилированы для обнаружения объектов, даже если
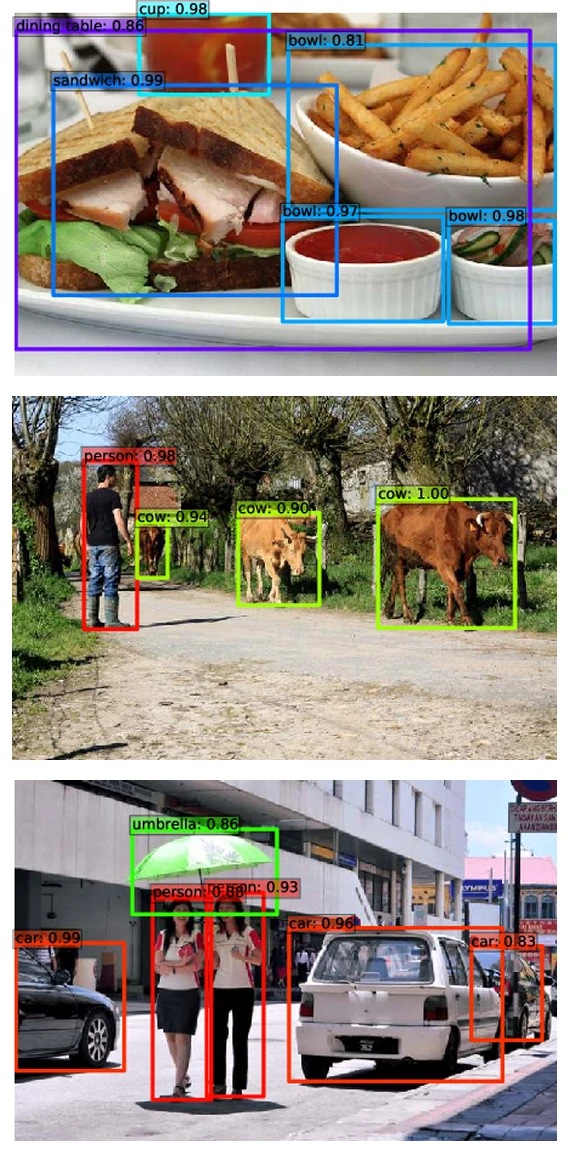
Рисунок 6.2
эта задача включает регрессию геометрических величин.
Во время обучения каждый истинный ограничивающий прямоугольник ассоциируется с его $s,h,w$ и порождает член потерь, состоящий из потерь кросс-энтропии для логитов и потерь регрессии, таких как MSE, для координат ограничивающего прямоугольника. Любой другой $s,h,w$ без совпадения с ограничивающим прямоугольником порождает только штраф кросс-энтропии для предсказания класса «нет объекта».
6.4 Семантическая сегментация (Semantic segmentation)
Наиболее детальной задачей предсказания для понимания изображений является семантическая сегментация, которая заключается в предсказании для каждого пикселя класса объекта, к которому он принадлежит. Это может быть достигнуто с помощью стандартной сверточной нейронной сети, которая выводит сверточную карту с количеством каналов, равным количеству классов, содержащую оцененные логиты для каждого пикселя.
В то время как стандартная остаточная сеть, например, может генерировать плотный выход с тем же разрешением, что и ее вход, как для обнаружения объектов, эта задача требует работы на нескольких масштабах. Это необходимо для того, чтобы любой объект или достаточно информативная подчасть, независимо от ее размера, была захвачена где-либо в модели представлением признаков в одной тензорной позиции. Следовательно, стандартные архитектуры для этой задачи уменьшают масштаб изображения с помощью серии сверточных слоев для увеличения рецептивного поля активаций и увеличивают его масштаб с помощью серии транспонированных сверточных слоев или других методов увеличения масштаба, таких как билинейная интерполяция, для выполнения предсказания с высоким разрешением.
Однако строгая архитектура уменьшения-увеличения масштаба не позволяет работать на детальном уровне

Рисунок 6.3
уровне при окончательном предсказании, поскольку весь сигнал был передан через представление низкого разрешения в какой-то момент. Модели, которые применяют такое последовательное уменьшение-увеличение масштаба, смягчают эти проблемы с помощью связей пропуска от слоев с определенным разрешением, перед уменьшением масштаба, к слоям с тем же разрешением, после увеличения масштаба [Long et al., 2014; Ronneberger et al., 2015]. Модели, которые делают это параллельно, после сверточного
основы, конкатенируют результирующее многомасштабное представление после увеличения масштаба, прежде чем сделать окончательное предсказание для каждого пикселя [Zhao et al., 2016].
Обучение осуществляется с помощью стандартной кросс-энтропии, суммированной по всем пикселям. Как и в случае обнаружения объектов, обучение может начинаться с сети, предварительно обученной на крупномасштабном наборе данных для классификации изображений, чтобы компенсировать ограниченную доступность истинной разметки сегментации.
6.5 Распознавание речи (Speech recognition)
Распознавание речи заключается в преобразовании звуковой выборки в последовательность слов. Исторически существовало множество подходов к этой проблеме, но концептуально простой и недавний, предложенный Radford et al. [2022], заключается в представлении ее как задачи перевода последовательность-в-последовательность и последующем решении с помощью стандартного Transformer на основе внимания, как описано в § 5.3.
Их модель сначала преобразует звуковой сигнал в спектрограмму, которая представляет собой одномерный ряд $T \times D$, кодирующий на каждом временном шаге вектор энергий в $D$ частотных полосах. Связанный текст кодируется с помощью токенизатора BPE (см. § 3.2).
Спектрограмма обрабатывается несколькими 1D-сверточными слоями, и полученное представление подается в кодировщик Transformer. Декодер непосредственно генерирует дискретную последовательность токенов, соответствующих одной из возможных задач, рассматриваемых во время обучения. Рассматриваются несколько целей: транскрипция английского или неанглийского текста, перевод с любого языка на английский, или обнаружение неречевых последовательностей, таких как фоновая музыка или окружающий шум.
Этот подход позволяет использовать чрезвычайно большие наборы данных, объединяющие несколько типов источников звука с разнообразной истинной разметкой.
Примечательно, что даже если конечной целью этого подхода является получение перевода, максимально детерминированного по заданному входному сигналу, формально это является выборкой текстового распределения, обусловленной звуковой выборкой, следовательно, процессом синтеза. Декодер, фактически, чрезвычайно похож на генеративную модель из § 7.1.
6.6 Текстово-изобразительные представления (Text-image representations)
Мощный подход к пониманию изображений заключается в изучении согласованных представлений изображений и текста таким образом, чтобы изображение или его текстовое описание отображались в один и тот же вектор признаков.
Contrastive Language-Image Pre-training (CLIP), предложенный Radford et al. [2021], объединяет кодировщик изображений $f$, который является ViT, и текстовый кодировщик $g$, который является GPT. См. § 5.3 для обоих.
Чтобы перепрофилировать GPT как текстовый кодировщик, вместо стандартной авторегрессионной модели они добавляют токен «конец предложения» во входную последовательность и используют представление этого токена в последнем слое в качестве встраивания. Его размерность составляет от 512 до 1024, в зависимости от конфигурации.
Эти две модели обучаются с нуля, используя набор данных из 400 миллионов пар изображение-текст $(i_k,t_k)$, собранных из Интернета. Процедура обучения следует стандартному подходу стохастического градиентного спуска по мини-пакетам, но основана на контрастивной функции потерь. Встраивания вычисляются для каждого изображения и каждого текста из $N$ пар в мини-пакете, и мера косинусного сходства вычисляется не только между встраиваниями текста и изображения из каждой пары, но и между парами, в результате чего получается матрица сходства $N \times N$:
$$l_{m,n} = f(i_m)\cdot g(t_n), \quad m = 1,...,N, n = 1,...,N$$
Модель обучается с помощью кросс-энтропии таким образом, что для всех $n$ значения $l_{1,n},...,l_{N,n}$, интерпретируемые как логиты, предсказывают $n$, и аналогично для $l_{n,1},...,l_{n,N}$. Это означает, что для всех $n,m$ таких, что $n \ne m$, сходство $l_{n,n}$ однозначно больше, чем $l_{n,m}$ и $l_{m,n}$.
После обучения эта модель может быть использована для предсказания с нулевым примером (zero-shot prediction), то есть для классификации сигнала в отсутствие обучающих примеров путем определения серии кандидатов классов с текстовыми описаниями и вычисления сходства встраивания изображения с встраиванием каждого из этих описаний (см. Рисунок 6.4).
Кроме того, поскольку текстовые описания часто детализированы, такая модель должна захватывать более богатое представление изображений и улавливать признаки, выходящие за рамки необходимого, например, для классификации. Это приводит к отличной производительности на сложных наборах данных, таких как ImageNet Adversarial [Hendrycks et al., 2019], который был специально разработан для ухудшения или удаления признаков, на которые полагаются стандартные предсказатели.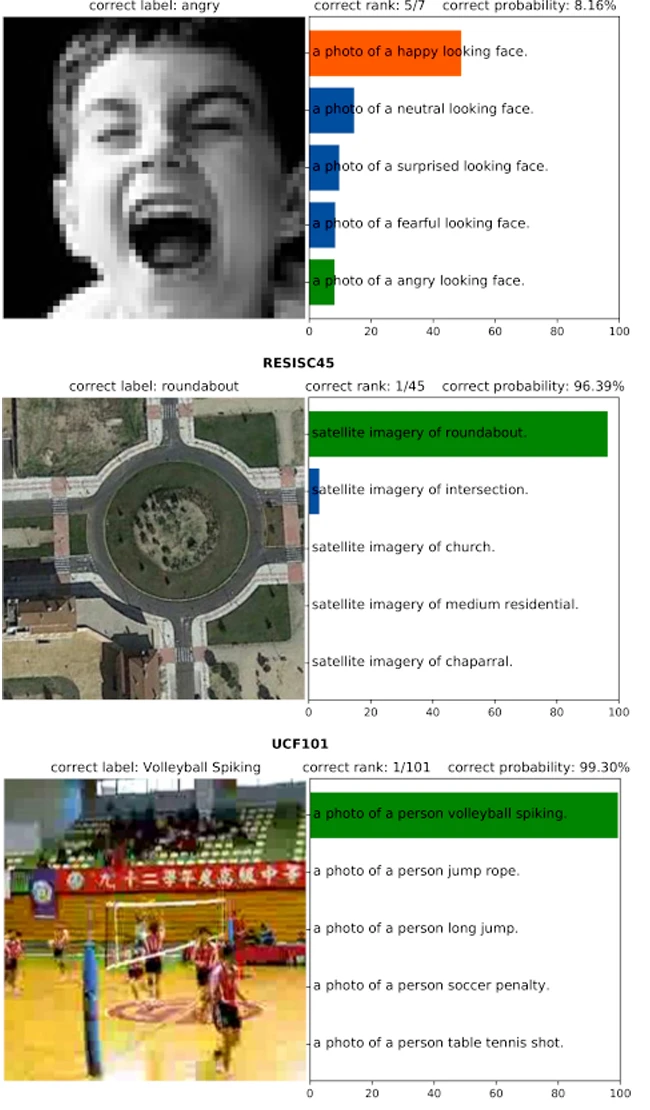
рисунок 6.4 Встраивание текста и изображения CLIP [Radford
et al., 2021] позволяет делать прогнозирование с нулевой точностью, предсказывая, какое встраивание описания класса наиболее соответствует встраиванию изображения
6.7 Обучение с подкреплением (Reinforcement learning)
Многие задачи, такие как стратегические игры или управление роботами, могут быть формализованы с помощью дискретного по времени процесса состояний $S_t$ и процесса вознаграждений $R_t$, которые могут модулироваться выбором действий $A_t$. Если $S_t$ является марковским, что означает, что оно само по себе несет столько же информации о будущем, сколько все прошлые состояния до этого момента, то такой объект является Марковским процессом принятия решений (MDP).
При заданном MDP целью классически является нахождение политики $\pi$ такой, что $A_t = \pi(S_t)$ максимизирует ожидание возврата, который является накопленным дисконтированным вознаграждением:
$$\mathbb{E} \left[ \sum_{t \ge 0} \gamma^t R_t \right]$$
для коэффициента дисконтирования $0 < \gamma < 1$.
Это стандартная установка обучения с подкреплением (RL), и она может быть решена путем введения оптимальной функции ценности состояния-действия $Q(s,a)$, которая представляет собой ожидаемый возврат, если мы выполним действие $a$ в состоянии $s$, а затем будем следовать оптимальной политике. Она предоставляет средство для вычисления оптимальной политики как $\pi(s) = \arg\max_a Q(s,a)$, и, благодаря марковскому предположению, она удовлетворяет
уравнению Беллмана:
$$Q(s,a) = \mathbb{E} \left[ R_t + \gamma \max_{a'} Q(S_{t+1},a') \middle| S_t = s, A_t = a \right] \quad (6.1)$$
из которого можно разработать процедуру обучения параметрической модели $Q(\cdot, \cdot ;w)$.
Чтобы применить эту структуру для игры в классические видеоигры Atari, Mnih et al. [2015] используют в качестве $S_t$ конкатенацию кадра в момент времени $t$ и трех предшествующих ему, так что марковское предположение является разумным, и используют для $Q$ модель, названную Deep Q-Network (DQN), состоящую из двух сверточных слоев и одного полносвязного слоя с одним выходным значением на каждое действие, следуя классической структуре LeNet (см. § 5.2).
Обучение достигается путем попеременного прохождения эпизодов и записи, а также построения мини-пакетов из кортежей $(s_n,a_n,r_n,s'_n) \sim (S_t,A_t,R_t,S_{t+1})$, взятых из записанных эпизодов и временных шагов, и минимизации
$$\mathcal{L}(w) = \frac{1}{N} \sum_{n=1}^N (Q(s_n,a_n;w)-y_n)^2 \quad (6.2)$$
с одной итерацией SGD, где $y_n = r_n$, если этот кортеж является концом эпизода, и $y_n = r_n + \gamma \max_a Q(s'_n,a;\bar{w})$ в противном случае.
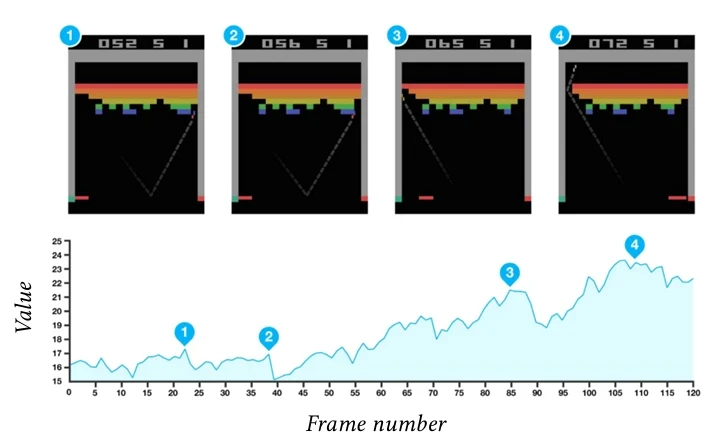
Рисунок 6.5 Этот график показывает эволюцию значения состояния V (St) = maxaQ(St,a) во время игры Breakout. Пики в точках времени (1) и (2) соответствуют
Здесь $\bar{w}$ — постоянная копия $w$, то есть градиент не распространяется через нее к $w$. Это необходимо, поскольку целевое значение в Уравнении 6.1 является ожиданием $y_n$, в то время как в Уравнении 6.2 используется сам $y_n$. Фиксация $w$ в $y_n$ приводит к лучшей аппроксимации желаемого градиента.
Ключевой проблемой является политика, используемая для сбора эпизодов. Mnih et al. [2015] просто используют $\epsilon$-жадную стратегию, которая заключается в выборе действия полностью случайным образом с вероятностью $\epsilon$, а в противном случае — оптимального действия $\arg\max_a Q(s,a)$. Введение небольшой доли случайности необходимо для содействия
исследованию.
Обучение проводится на десяти миллионах кадров, что соответствует чуть менее восьми дням игры. Обученная сеть вычисляет точные оценки ценности состояний (см. Рисунок 6.5) и достигает производительности человека на большинстве из 49 игр, использованных в экспериментальной проверке.
Глава 7
Синтез
Вторая категория приложений, отличная от предсказания, — это синтез. Она заключается в подгонке модели плотности к обучающим выборкам и предоставлении средств для выборки из этой модели.
7.1 Генерация текста (Text generation)
Стандартный подход к синтезу текста — использование авторегрессионной модели, основанной на механизме внимания. Очень успешной моделью, предложенной Radford et al. [2018], является GPT, которую мы описали в § 5.3.
Эта архитектура была использована для очень больших моделей, таких как GPT-3 от OpenAI с 175 миллиардами параметров [Brown et al., 2020]. Она состоит из 96 блоков самовнимания, каждый с 96 головами, и обрабатывает токены размерности 12 288, с скрытой размерностью 49 512 в MLP блоков внимания.
Когда такая модель обучается на очень большом наборе данных, она становится Большой языковой моделью (LLM), которая демонстрирует чрезвычайно мощные свойства. Помимо синтаксической и грамматической структуры языка, она должна интегрировать очень разнообразные знания, например, для предсказания слова, следующего за «Столица Японии — », «если вода нагрета до 100 градусов по Цельсию, она превращается в », или «потому что ее щенок был болен, Джейн была ».
Это приводит, в частности, к способности решать задачи предсказания с малым количеством примеров (few-shot prediction), когда доступно лишь небольшое количество обучающих примеров, как показано на Рисунке 7.1. Что еще более удивительно, при использовании тщательно составленного запроса она может демонстрировать способности

Рисунок 7.1 (Примеры прогнозирования с несколькими выстрелами с моделью GPT из 120 миллионов параметров от Hugging Face. В подсказке каждого примера начало предложения было указано как , а модель сгенерировала часть, выделенную жирным шрифтом.)
способности к ответу на вопросы, решению задач и рассуждениям «цепочкой мыслей» (chain-of-thought), которые кажутся жутко близкими к высокоуровневым рассуждениям [Chowdhery et al., 2022; Bubeck et al., 2023].
Благодаря этим замечательным возможностям, эти модели иногда называются фундаментальными моделями [Bommasani et al., 2021].
Однако, несмотря на то, что она интегрирует очень большой объем знаний, такая модель может быть неадекватной
адекватной для практических приложений, в частности, при взаимодействии с пользователями. Во многих ситуациях требуются ответы, соответствующие статистике полезного диалога с помощником. Это отличается от статистики доступных больших обучающих наборов, которые объединяют романы, энциклопедии, сообщения форумов и записи блогов.
Эта неточность устраняется путем тонкой настройки такой языковой модели (см. § 3.6). Текущая доминирующая стратегия — обучение с подкреплением на основе обратной связи от человека (RLHF) [Ouyang et al., 2022], которое заключается в создании небольших размеченных обучающих наборов путем просьбы к пользователям либо писать ответы, либо предоставлять оценки сгенерированных ответов. Первое может быть использовано как есть для тонкой настройки языковой модели, а второе может быть использовано для обучения сети вознаграждения, которая предсказывает оценку, и использовать ее в качестве цели для тонкой настройки языковой модели с помощью стандартного подхода обучения с подкреплением.
7.2 Генерация изображений (Image generation)
Было разработано множество глубоких методов для моделирования и выборки из высокоразмерной плотности. Мощный подход к синтезу изображений основан на инвертировании процесса диффузии. Такая генеративная модель называется, несколько некорректно, диффузионной моделью.
Принцип заключается в аналитическом определении процесса, который постепенно ухудшает любой образец и, следовательно, преобразует сложную и неизвестную плотность данных в простую и хорошо известную плотность, такую как нормальное распределение, и обучении глубокой архитектуры для инвертирования этого процесса деградации [Ho et al., 2020].
При заданном фиксированном $T$ процесс диффузии определяет распределение вероятностей по сериям из $T+1$ изображений следующим образом: выбирается $x_0$ равномерно из набора данных, а затем последовательно выбирается $x_{t+1} \sim p(x_{t+1} | x_t)$, $t = 0,...,T-1$, где условное распределение $p$ определяется аналитически и таким образом, что оно постепенно стирает структуру, которая была в $x_0$. Установка должна настолько ухудшить сигнал, что распределение $p(x_T)$ имеет известную аналитическую форму, из которой можно производить выборку.
Например, Ho et al. [2020] нормализуют данные так, чтобы они имели среднее 0 и дисперсию 1, и их

Рисунок 7.2(Синтез изображения с шумоподавляющей диффузией
процесс диффузии состоит в добавлении небольшого белого шума и повторной нормализации дисперсии до 1. Этот процесс экспоненциально уменьшает важность $x_0$, и плотность $x_t$ может быть быстро аппроксимирована нормальным распределением.
Шумоподавитель $f$ — это глубокая архитектура, которая должна моделировать и позволять производить выборку из $f(x_{t-1},x_t,t;w) \simeq p(x_{t-1} | x_t)$. Можно показать, благодаря вариационной границе, что если этот одношаговый обратный процесс достаточно точен, выборка $x_T \sim p(x_T)$ и шумоподавление $T$ шагов с помощью $f$ приводит к $x_0$, которое следует $p(x_0)$.
Обучение $f$ может быть достигнуто путем генерации большого количества последовательностей $x^{(n)}_0,...,x^{(n)}_T$, выбора $t_n$ в каждой и максимизации
$$\sum_n \log f(x^{(n)}_{t_n-1},x^{(n)}_{t_n},t_n;w)$$
Учитывая их процесс диффузии, Ho et al. [2020] имеют шумоподавление вида:
$$x_{t-1} | x_t \sim \mathcal{N}(x_t + f(x_t,t;w);\sigma_t) \quad (7.1)$$
где $\sigma_t$ определяется аналитически.
На практике такая модель изначально галлюцинирует структуры благодаря чистой случайности в случайном шуме, и
затем постепенно строит больше элементов, которые возникают из шума, усиливая наиболее вероятное продолжение полученного до сих пор изображения.
Этот подход может быть расширен на синтез с текстовым условием для генерации изображений, соответствующих описанию. Например, Nichol et al. [2021] добавляют к среднему значению распределения шумоподавления из Уравнения 7.1 смещение, направленное на увеличение оценки CLIP-соответствия (см. § 6.6) между созданным изображением и условием в виде текстового описания.
Глава 8
Вычислительный раскол (The Compute Schism)
Масштаб глубоких архитектур критически важен для их производительности, и, как мы видели в § 3.7, большие языковые модели, в частности, могут требовать объемов памяти и вычислений, значительно превышающих возможности потребительского оборудования.
В то время как обучение такой модели с нуля требует ресурсов, доступных только крупным корпорациям или государственным организациям, были разработаны методы, позволяющие осуществлять инференс и адаптацию к конкретным задачам при сильных ограничениях на ресурсы. Возможность запускать модели локально, а не через провайдера, может быть очень желательной по причинам стоимости или конфиденциальности.
8.1 Проектирование запросов (Prompt Engineering)
Простейшая стратегия для специализации или улучшения большой языковой модели с ограниченным вычислительным бюджетом — это использование проектирования запросов (prompt engineering), то есть тщательного составления начала текстовой последовательности для смещения авторегрессионного процесса [Sahoo et al., 2024]. Этот подход переносит часть информации, традиционно закодированной в параметрах модели, во входные данные.
Мы видели в § 7.1 простой пример few-shot prediction, использования LLM для задачи классификации текста без тонкой настройки. Длинный и сложный запрос позволяет обобщить эту стратегию на более сложные задачи.
Поскольку роль запроса заключается в использовании «хороших» смещений, присутствовавших в обучающем наборе, он выигрывает от удивительных стратегий, таких как утверждение, что ответ сгенерирован квалифицированным профессионалом [Xu et al., 2023].
Размер контекста языковой модели, то есть количество токенов, с которыми она может работать, напрямую модулирует количество информации, которое может быть предоставлено в запросе. Это в основном ограничено вычислительной стоимостью стандартных моделей внимания, которая квадратична по размеру контекста (см. § 4.8).

Рисунок 8.1 (Пример цепочки мыслей для улучшения ответа базовой модели Llama-3-8B. В двух примерах начало текста обычным шрифтом является подсказкой, а сгенерированная часть выделена жирным шрифтом. Генерация без цепочки мыслей (вверху) приводит к неправильному ответу, тогда как генерация с ней (внизу) генерирует правильный ответ, явно производя несколько простых арифметических операций.)
Цепочка мыслей (Chain of Thought)
Замечательный тип запросов направлен на то, чтобы модель генерировала промежуточные шаги перед тем, как сгенерировать сам ответ.
Такая цепочка мыслей состоит из последовательных шагов, которые проще, следовательно, были лучше смоделированы во время обучения и предсказываются более детерминированно [Wei et al., 2022; Kojima et al., 2022]. Пример см. на Рисунке 8.1.
Генерация с дополненным поиском (Retrieval-Augmented Generation)
Проектирование запросов также может быть использовано для подключения языковой модели к внешней базе знаний. Оно играет роль интеллектуального интерфейса, позволяющего пользователю формулировать вопросы на естественном языке и получать ответ, объединяющий информацию, которая не закодирована в параметрах модели [Lewis et al., 2020].
Для такой генерации с дополненным поиском (RAG) используется модель встраивания для извлечения документов, встраивание которых коррелирует с запросом пользователя. Затем строится запрос путем объединения этих извлеченных документов с инструкциями по их объединению, и генеративная модель выдает ответ пользователю.
8.2 Квантование (Quantization)
Хотя обучение или генерация нескольких потоков могут выиграть от высокопроизводительных параллельных вычислительных устройств, развертывание большой языковой модели для индивидуального использования обычно требует однопоточного инференса, который гораздо больше ограничен размером памяти и скоростью, чем вычислениями.
Как указано в § 2.1, параметры, активации и градиенты обычно кодируются 32 или 16 битами. Точность, которую это обеспечивает, необходима для обучения, чтобы позволить накапливаться постепенным изменениям.
Однако, поскольку активации являются суммами многих слагаемых, квантование во время инференса смягчается эффектом усреднения. Это еще более верно для больших архитектур, и модели, квантованные до 6 или 4 бит на параметр, демонстрируют замечательную производительность. Кроме того, квантование, помимо уменьшения занимаемой памяти, также значительно повышает скорость инференса.
Это стимулировало разработку программного обеспечения для квантования существующих моделей с помощью квантования после обучения (Post-Training Quantization) и их запуска в режиме однопоточного инференса на потребительском оборудовании, таком как llama.cpp [Llama.cpp, 2023]. Этот фреймворк реализует несколько форматов, которые применяют специфические
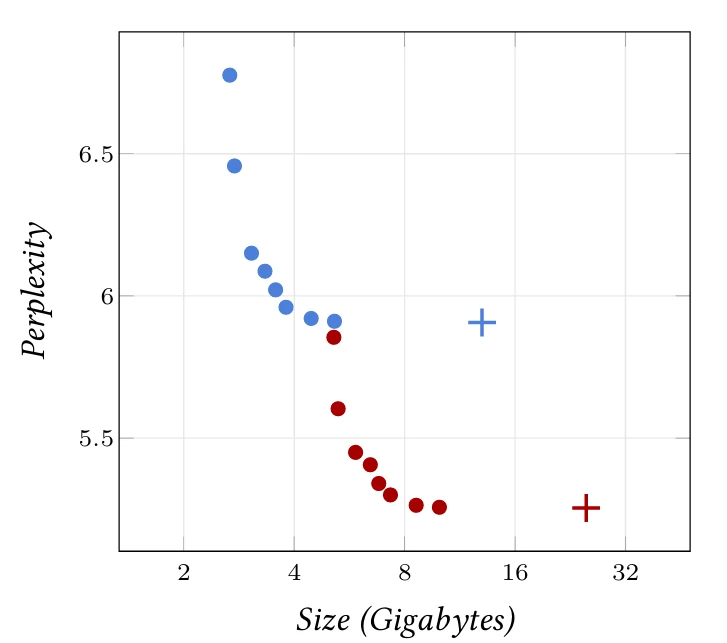
Рисунок 8.2 (Perplexity 4 8 Размер (Гигабайт) 16 32 квантованных версий языковых моделей Llama-7B (синий) и 13B (красный) [Touvron et al., 2023] в корпусе викитекста, как функция отпечатка памяти параметров. Крестики — это исходные модели FP16, а точки соответствуют различным уровням квантования с llama.cpp [Llama.cpp, 2023])
уровни квантования для различных матриц весов языковой модели. Например, квантование может использовать больше битов для весов $W^V$ блоков внимания и для весов блоков прямого распространения.
Примером квантования llama.cpp является Q4_1.
Он индивидуально квантует подблоки из 32 записей исходной матрицы весов, сохраняя для каждого масштабный коэффициент $d$ и смещение $m$ в исходном кодировании FP16, и кодируя каждую запись $x$ 4 битами в виде значения $q \in \{0,...,2^4-1\}$. Результирующее деквантованное значение $\tilde{x} = dq+m$.
Такой блок изначально был закодирован как 32 значения в FP16, следовательно, 64 байта, тогда как квантованная версия требует 4 байта для $q$ и $m$ и $32 \cdot 4 = 16$ байт для записей, следовательно, всего 20 байт.
Такое агрессивное квантование, как ни удивительно, ухудшает производительность моделей лишь незначительно, как показано на Рисунке 8.2.
Альтернативой квантованию после обучения является квантование с учетом обучения (Quantization-Aware Training), которое применяет квантование во время прямого прохода, но сохраняет высокоточное кодирование параметров и градиентов, и распространяет градиенты во время обратного прохода так, как если бы квантования не было [Ma et al., 2024].
8.3 Адаптеры (Adapters)
Как мы видели в § 3.6, тонкая настройка является ключевой стратегией повторного использования предварительно обученных моделей. Поскольку ее целью являются лишь незначительные изменения в существующей модели, были разработаны техники, добавляющие компоненты с небольшим количеством параметров, называемые адаптерами, к предварительно обученной архитектуре, и замораживающие все исходные параметры [Houlsby et al., 2019].
Текущим доминирующим методом является адаптация низкого ранга (Low-Rank Adaptation, LoRA), которая добавляет низкоранговые поправки к некоторым матрицам весов модели [Hu et al., 2021].
Формально, при заданном линейном преобразовании вида $XW^T$, где $X$ — тензор активаций размера $N \times D$ для пакета из $N$ образцов, а $W$ — матрица весов размера $C \times D$, адаптер LoRA заменяет эту операцию на $X(W+BA)^T$, где $A$ и $B$ — две обучаемые матрицы размера $R \times D$ и $C \times R$ соответственно, с $R \ll \min(C,D)$, а матрица $W$ удаляется из обучаемых параметров. Матрица $A$ инициализируется случайными гауссовыми значениями, а $B$ устанавливается в ноль, так что тонкая настройка начинается с модели, которая вычисляет выход, идентичный выходу исходной модели.
Общее количество параметров для оптимизации с помощью этого подхода обычно составляет всего несколько процентов от количества параметров в исходной модели.
Стандартная процедура тонкой настройки трансформера с такими адаптерами заключается в изменении только матриц весов в блоках внимания и сохранении MLP блоков прямого распространения неизмененными. Та же стратегия успешно использовалась для тонкой настройки диффузионных шумоподавляющих моделей путем тонкой настройки блоков внимания, ответственных за текстовое условие.
Поскольку тонкая настройка с адаптерами LoRA резко уменьшает количество обучаемых параметров, она снижает объем памяти, требуемый оптимизаторами, такими как Adam, которые обычно хранят два скользящих средних на параметр для оптимизации. Кроме того, она немного снижает вычислительную нагрузку во время обратного прохода.
Для коммерческих приложений, требующих большого количества тонко настроенных моделей, пары $AB$ могут храниться отдельно от исходной модели, которая должна храниться только один раз. И, наконец, в отличие от других типов адаптеров, модификации могут быть интегрированы в исходную архитектуру просто путем добавления $AB$ к $W$, что приводит к архитектуре и количеству параметров для инференса
строго идентичному базовой модели.
Мы видели, что квантование ухудшает точность моделей лишь незначительно. Однако градиентный спуск требует высокой точности как градиента, так и обученных параметров, чтобы позволить накопление малых изменений. Подход QLoRA объединяет квантованную базовую модель и неквантованную адаптацию низкого ранга (Low-Rank Adaptation), чтобы еще больше уменьшить требования к памяти [Dettmers et al., 2023].
8.4 Слияние моделей (Model merging)
Альтернатива методам тонкой настройки и запросов, рассмотренным в предыдущих разделах, заключается в объединении нескольких моделей с различными возможностями в одну, без дополнительного обучения.
Слияние моделей основано на совместимости нескольких тонко настроенных версий базовой модели.
Ilharco et al. [2022] показали, что модели, полученные путем тонкой настройки базовой модели CLIP на нескольких наборах данных для классификации изображений, могут быть объединены в пространстве параметров, где они демонстрируют свойства арифметики задач (Task Arithmetic).
Формально, пусть $\theta$ — вектор параметров предварительно обученной модели, и для $t = 1,...,T$, пусть $\theta_t$ и $\tau_t = \theta_t - \theta$ будут соответственно параметрами после тонкой настройки на задаче $t$ и соответствующим остатком. Эксперименты показывают, что модель с параметрами $\theta+\tau_1 + \cdots + \tau_T$ демонстрирует мультизадачные возможности. Аналогично, вычитание $\tau_t$ ухудшает производительность на соответствующей задаче.
Были разработаны методы для уменьшения интерференции между различными остатками и улучшения производительности при увеличении числа
задач [Yadav et al., 2023; Yu et al., 2023].
Альтернативой слиянию моделей в пространстве параметров является их повторное объединение на уровне слоев. Akiba et al. [2024] объединяют слияние параметров и повторное объединение слоев, и полагаются на стохастическую оптимизацию для решения проблемы комбинаторного взрыва. Эксперименты с тремя тонко настроенными версиями Mistral-7B [Jiang et al., 2023] показывают, что объединение этих двух стратегий слияния превосходит каждую из них по отдельности.
Недостающие фрагменты (The Missing Bits)
Для краткости этот том пропускает множество важных тем, в частности:
Рекуррентные нейронные сети (Recurrent Neural Networks)
До того как модели внимания показали лучшую производительность, рекуррентные нейронные сети (RNN) были стандартным подходом для работы с временными последовательностями, такими как текст или звуковые выборки. Эти архитектуры обладают внутренним скрытым состоянием, которое обновляется каждый раз, когда обрабатывается компонент последовательности. Их основными компонентами являются слои, такие как LSTM [Hochreiter and Schmidhuber, 1997] или GRU [Cho et al., 2014].
Обучение рекуррентной архитектуры сводится к ее разворачиванию во времени, что приводит к длинной композиции операторов. Это исторически подтолкнуло к разработке ключевых техник, используемых теперь для глубоких архитектур, таких как выпрямители (rectifiers) и gating, форма связей пропуска (skip connections), которые модулируются
модулируются динамически.
Одним из ключевых недостатков традиционных рекуррентных архитектур является то, что структура вычисления $x_{t+1} = f(x_t)$ требует последовательной обработки входной последовательности, что занимает время, пропорциональное $T$. В отличие от этого, трансформеры, например, могут использовать преимущества параллельных вычислений, что приводит к постоянному времени, если доступно достаточно вычислительных блоков.
Это решается архитектурами, такими как QRNN [Bradbury et al., 2016], S4 [Gu et al., 2021] или Mamba [Gu and Dao, 2023], чьи рекуррентные операции являются аффинными, так что сами $f^t$, и, следовательно, $x_t = f^t(x_0)$, могут быть вычислены параллельно, что приводит к постоянному времени, если $f$ не зависит от $t$, и $\log T$ в противном случае, опять же, если доступно достаточно параллельных вычислительных блоков.
Автокодировщик (Autoencoder)
Автокодировщик — это модель, которая отображает входной сигнал, возможно, большой размерности, в латентное представление низкой размерности, а затем отображает его обратно в исходный сигнал, гарантируя, что информация была сохранена. Мы видели его в § 6.1 для шумоподавления, но его также можно использовать для автоматического обнаружения значимого низкоразмерного
параметризации многообразия данных.
Вариационный автокодировщик (VAE), предложенный Kingma and Welling [2013], является генеративной моделью с похожей структурой. Он накладывает, через функцию потерь, предопределенное распределение на латентное представление. Это позволяет после обучения генерировать новые образцы путем выборки латентного представления в соответствии с этим наложенным распределением и последующего отображения через декодер.
Генеративно-состязательные сети (Generative Adversarial Networks)
Другой подход к моделированию плотности — это генеративно-состязательные сети (GAN), введенные Goodfellow et al. [2014]. Этот метод объединяет генератор, который принимает случайный вход, следующий фиксированному распределению, и производит структурированный сигнал, такой как изображение, и дискриминатор, который принимает образец в качестве входа и предсказывает, происходит ли он из обучающего набора или был сгенерирован генератором.
Обучение оптимизирует дискриминатор для минимизации стандартной функции потерь кросс-энтропии, а генератор — для максимизации потерь дискриминатора. Можно показать, что в равновесии генератор производит образцы, неразличимые от реальных данных. На практике, когда градиент проходит через дискриминатор к генератору, он информирует последнего о признаках, которые использует дискриминатор, и которые необходимо учесть.
Графовые нейронные сети (Graph Neural Networks)
Многие приложения требуют обработки сигналов, которые не организованы регулярно в виде сетки. Например, белки, 3D-сетки, географические местоположения или социальные взаимодействия более естественно структурированы как графы. Стандартные сверточные сети или даже модели внимания плохо приспособлены для обработки таких данных, и инструментом выбора для такой задачи являются графовые нейронные сети (GNN) [Scarselli et al., 2009].
Эти модели состоят из слоев, которые вычисляют активации в каждом узле, линейно объединяя активации, расположенные в его ближайших соседних узлах. Эта операция очень похожа на стандартную свертку, за исключением того, что структура данных не отражает никакой геометрической информации, связанной с векторами признаков, которые они несут.
Самостоятельное обучение (Self-supervised training)
Как указано в § 7.1, несмотря на то, что большие языковые модели, обученные на больших неразмеченных наборах данных, таких как GPT (см. § 5.3), обучаются только предсказывать следующее слово, они способны решать различные задачи, такие как определение грамматической роли слова, ответы на вопросы или даже перевод с одного языка на другой [Radford et al., 2019].
Такие модели представляют собой одну категорию более широкого класса методов, которые подпадают под название самостоятельного обучения (self-supervised learning) и пытаются использовать преимущества неразмеченных наборов данных [Balestriero et al., 2023].
Ключевой принцип этих методов состоит в определении задачи, которая не требует меток, но требует представлений признаков, полезных для реальной задачи интереса, для которой существует небольшой размеченный набор данных. В компьютерном зрении, например, признаки изображений могут быть оптимизированы таким образом, чтобы они были инвариантны к преобразованиям данных, которые не изменяют семантическое содержание изображения, при этом статистически некоррелированны [Zbontar et al., 2021].
Как в NLP, так и в компьютерном зрении мощной общей стратегией является обучение модели восстановлению частей сигнала, которые были замаскированы [Devlin et al., 2018; Zhou et al., 2021].
Другие статьи по этой теме:
- 100 Страниц о машинном обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения