Глава 4. Анатомия алгоритма обучения
4.1 Строительные блоки алгоритма обучения
Возможно, вы заметили, читая предыдущую главу, что каждый алгоритм обучения, который мы видели, состоял из трех частей:
- функции потерь;
- критерия оптимизации на основе функции потерь (например, функции стоимости); и
- процедуры оптимизации, использующей обучающие данные для нахождения решения критерия оптимизации.
Это строительные блоки любого алгоритма обучения. В предыдущей главе вы видели, что некоторые алгоритмы были разработаны для явной оптимизации конкретного критерия (как линейная, так и логистическая регрессия, SVM). Другие, включая обучение деревьев решений и kNN, оптимизируют критерий неявно. Обучение деревьев решений и kNN относятся к числу старейших алгоритмов машинного обучения и были изобретены экспериментально на основе интуиции, без конкретного глобального критерия оптимизации, и (как это часто бывало в истории науки) критерии оптимизации были разработаны позже, чтобы объяснить, почему эти алгоритмы работают.
Читая современную литературу по машинному обучению, вы часто сталкиваетесь с упоминаниями градиентного спуска (gradient descent) или стохастического градиентного спуска (stochastic gradient descent). Это два наиболее часто используемых алгоритма оптимизации в случаях, когда критерий оптимизации дифференцируем.
Градиентный спуск — это итерационный алгоритм оптимизации для нахождения минимума функции. Чтобы найти локальный минимум функции с помощью градиентного спуска, начинают с некоторой случайной точки и делают шаги, пропорциональные отрицательному градиенту (или приблизительному градиенту) функции в текущей точке.
Градиентный спуск можно использовать для поиска оптимальных параметров для линейной и логистической регрессии, SVM, а также нейронных сетей, которые мы рассмотрим позже. Для многих моделей, таких как логистическая регрессия или SVM, критерий оптимизации является выпуклым (convex). Выпуклые функции имеют только один минимум, который является глобальным. Критерии оптимизации для нейронных сетей не являются выпуклыми, но на практике достаточно даже нахождения локального минимума.
Давайте посмотрим, как работает градиентный спуск.
4.2 Градиентный спуск
В этом разделе я демонстрирую, как градиентный спуск находит решение задачи линейной регрессии1. Я иллюстрирую свое описание кодом на Python, а также графиками, которые показывают, как улучшается решение после нескольких итераций градиентного спуска. Я использую набор данных только с
одним признаком. Однако критерий оптимизации будет иметь два параметра: \(w\) и \(b\). Расширение на многомерные обучающие данные просто: у вас есть переменные \(w^{(1)}\), \(w^{(2)}\) и \(b\) для двумерных данных, \(w^{(1)}\), \(w^{(2)}\), \(w^{(3)}\) и \(b\) для трехмерных данных и так далее.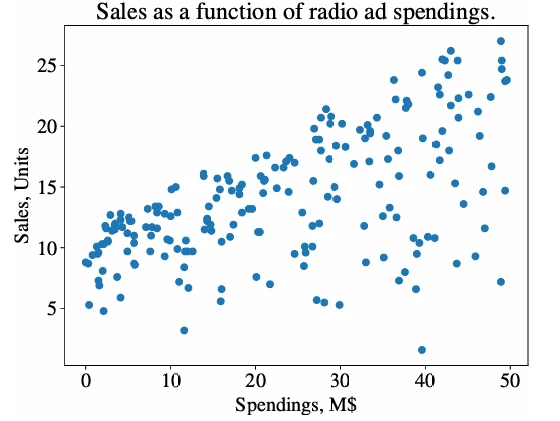
Чтобы привести практический пример, я использую реальный набор данных (можно найти на вики книги) со следующими столбцами: Расходы различных компаний на радиорекламу каждый год и их годовые Продажи в единицах товара. Мы хотим построить модель регрессии, которую можно использовать для прогнозирования проданных единиц на основе того, сколько компания тратит на радиорекламу. Каждая строка в наборе данных представляет одну конкретную компанию:
| Компания | Расходы, М$ | Продажи, Единицы |
|---|---|---|
| 1 | 37.8 | 22.1 |
| 2 | 39.3 | 10.4 |
| 3 | 45.9 | 9.3 |
| 4 | 41.3 | 18.5 |
| .. | .. | .. |
У нас есть данные по 200 компаниям, то есть 200 обучающих примеров в форме \((x_i, y_i) = (\text{Расходы}_i, \text{Продажи}_i)\). Рисунок 1 (в pdf) показывает все примеры на 2D-графике.
Помните, что модель линейной регрессии выглядит так: \(f(x) = wx + b\). Мы не знаем, каковы оптимальные значения для \(w\) и \(b\), и хотим изучить их из данных. Для этого
мы ищем такие значения \(w\) и \(b\), которые минимизируют среднеквадратичную ошибку:
\[ l \stackrel{\text{def}}{=} \frac{1}{N} \sum_{i=1}^N (y_i - (wx_i + b))^2. \]Градиентный спуск начинается с вычисления частной производной для каждого параметра:
\begin{align*} \frac{\partial l}{\partial w} &= \frac{1}{N} \sum_{i=1}^N -2x_i(y_i - (wx_i + b)); \\ \frac{\partial l}{\partial b} &= \frac{1}{N} \sum_{i=1}^N -2(y_i - (wx_i + b)). \quad (1) \end{align*}Чтобы найти частную производную члена \((y_i - (wx + b))^2\) по \(w\), я применил правило цепочки. Здесь у нас есть цепочка \(f = f_2(f_1)\), где \(f_1 = y_i - (wx + b)\) и \(f_2 = f_1^2\). Чтобы найти частную производную \(f\) по \(w\), мы должны сначала найти частную производную \(f\) по \(f_2\), которая равна \(2(y_i - (wx + b))\) (из матанализа мы знаем, что производная \(\frac{\partial}{\partial x} x^2 = 2x\)), а затем мы должны умножить ее на частную производную \(y_i - (wx + b)\) по \(w\), которая равна \(-x\). Таким образом, в целом \(\frac{\partial l}{\partial w} = \frac{1}{N} \sum_{i=1}^N -2x_i(y_i - (wx_i + b))\). Аналогичным образом была вычислена частная производная \(l\) по \(b\), \(\frac{\partial l}{\partial b}\).
Градиентный спуск выполняется по эпохам (epochs). Эпоха заключается в полном использовании обучающего набора для обновления каждого параметра. В начале, в первую эпоху, мы инициализируем2 \(w \leftarrow 0\) и \(b \leftarrow 0\). Частные производные, \(\frac{\partial l}{\partial w}\) и \(\frac{\partial l}{\partial b}\), заданные ур. 1, равны соответственно \(\frac{-2}{N} \sum_{i=1}^N x_i y_i\) и \(\frac{-2}{N} \sum_{i=1}^N y_i\). В каждую эпоху мы обновляем \(w\) и \(b\), используя частные производные. Скорость обучения (learning rate) \(\alpha\) контролирует размер обновления:
\begin{align*} w &\leftarrow w - \alpha \frac{\partial l}{\partial w}; \\ b &\leftarrow b - \alpha \frac{\partial l}{\partial b}. \quad (2) \end{align*}Мы вычитаем (в отличие от добавления) частные производные из значений параметров, потому что производные являются индикаторами роста функции. Если производная положительна в некоторой точке3, то функция растет в этой точке. Поскольку мы хотим минимизировать целевую функцию,
когда производная положительна, мы знаем, что нам нужно двигать наш параметр в противоположном направлении (влево по оси координат). Когда производная отрицательна (функция убывает), нам нужно двигать наш параметр вправо, чтобы еще больше уменьшить значение функции. Вычитание отрицательного значения из параметра перемещает его вправо.
На следующей эпохе мы пересчитываем частные производные, используя ур. 1 с обновленными значениями \(w\) и \(b\); мы продолжаем процесс до сходимости. Обычно требуется много эпох, пока мы не начнем видеть, что значения \(w\) и \(b\) не сильно меняются после каждой эпохи; тогда мы останавливаемся.
Трудно представить инженера по машинному обучению, который не использует Python. Итак, если вы ждали подходящего момента, чтобы начать изучать Python, то этот момент настал. Ниже я показываю, как запрограммировать градиентный спуск на Python.
Функция, которая обновляет параметры \(w\) и \(b\) в течение одной эпохи, показана ниже:
1 def update_w_and_b(spendings, sales, w, b, alpha):
2 dl_dw = 0.0
3 dl_db = 0.0
4 N = len(spendings)
5
6 for i in range(N):
7 dl_dw += -2*spendings[i]*(sales[i] - (w*spendings[i] + b))
8 dl_db += -2*(sales[i] - (w*spendings[i] + b))
9
10 # update w and b
11 w = w - (1/float(N))*dl_dw*alpha
12 b = b - (1/float(N))*dl_db*alpha
13
14 return w, b
Функция, которая выполняет цикл по нескольким эпохам, показана ниже:
15 def train(spendings, sales, w, b, alpha, epochs):
16 for e in range(epochs):
17 w, b = update_w_and_b(spendings, sales, w, b, alpha)
18
19 # log the progress
20 if e % 400 == 0:
21 print("epoch:", e, "loss: ", avg_loss(spendings, sales, w, b))
22
23 return w, b
Функция avg_loss в приведенном выше фрагменте кода — это функция, которая вычисляет среднеквадратичную ошибку. Она определяется как: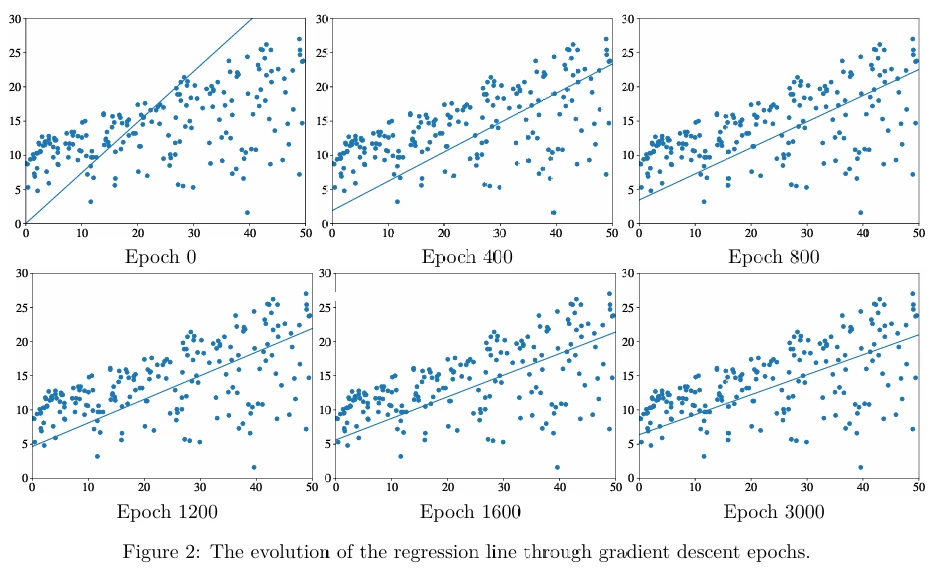
25 def avg_loss(spendings, sales, w, b):
26 N = len(spendings)
27 total_error = 0.0
28 for i in range(N):
29 total_error += (sales[i] - (w*spendings[i] + b))**2
30 return total_error / float(N)
Если мы запустим функцию train для \(\alpha = 0.001\), \(w = 0.0\), \(b = 0.0\) и 15 000 эпох, мы увидим следующий вывод (показан частично):
epoch: 0 loss: 92.32078294903626
epoch: 400 loss: 33.79131790081576
epoch: 800 loss: 27.9918542960729
epoch: 1200 loss: 24.33481690722147
epoch: 1600 loss: 22.028754937538633
...
epoch: 2800 loss: 19.07940244306619
Вы можете видеть, что средняя потеря уменьшается по мере того, как функция train проходит по эпохам. Рисунок 2 (в pdf) показывает эволюцию линии регрессии по эпохам градиентного спуска.
Наконец, как только мы нашли оптимальные значения параметров \(w\) и \(b\), единственная недостающая часть — это функция, которая делает предсказания:
31 def predict(x, w, b):
32 return w*x + b
Попробуйте выполнить следующий код:
33 w, b = train(x, y, 0.0, 0.0, 0.001, 15000)
34 x_new = 23.0
35 y_new = predict(x_new, w, b)
36 print(y_new)
Вывод будет 13.97.
Градиентный спуск чувствителен к выбору скорости обучения \(\alpha\). Он также медленный для больших наборов данных. К счастью, было предложено несколько значительных улучшений этого алгоритма.
Мини-пакетный стохастический градиентный спуск (minibatch SGD) — это версия алгоритма, которая ускоряет вычисления путем аппроксимации градиента с использованием меньших пакетов (подмножеств) обучающих данных. Сам SGD имеет различные «улучшения». Adagrad — это версия SGD, которая масштабирует \(\alpha\) для каждого параметра в соответствии с историей градиентов. В результате \(\alpha\) уменьшается для очень больших градиентов и наоборот. Momentum — это метод, который помогает ускорить SGD, ориентируя градиентный спуск в релевантном направлении и уменьшая колебания. При обучении нейронных сетей очень часто используются варианты SGD, такие как RMSprop и Adam.
Обратите внимание, что градиентный спуск и его варианты не являются алгоритмами машинного обучения. Это решатели задач минимизации, в которых функция для минимизации имеет градиент (в большинстве точек своей области определения).
4.3 Как работают инженеры машинного обучения
Если вы не являетесь научным исследователем или не работаете в огромной корпорации с большим бюджетом на НИОКР, вы обычно не реализуете алгоритмы машинного обучения самостоятельно. Вы также не реализуете градиентный спуск или какой-либо другой решатель. Вы используете библиотеки, большинство из которых имеют открытый исходный код. Библиотека — это коллекция алгоритмов и вспомогательных инструментов, реализованных с учетом стабильности и эффективности. Наиболее часто используемой на практике библиотекой машинного обучения с открытым исходным кодом является scikit-learn. Она написана на Python и C. Вот как вы делаете линейную регрессию в scikit-learn:
1 def train(x, y):
2 from sklearn.linear_model import LinearRegression
3 model = LinearRegression().fit(x,y)
4 return model
5
6 model = train(x,y)
7
8 x_new = 23.0
9 y_new = model.predict(x_new) # x_new must be a list or NumPy array
10 print(y_new)
Вывод снова будет 13.97. Легко, правда? Вы можете заменить LinearRegression на какой-либо другой тип алгоритма обучения регрессии, не изменяя ничего другого. Он просто работает. То же самое можно сказать и о классификации. Вы можете легко заменить алгоритм LogisticRegression на алгоритм SVC (это название scikit-learn для алгоритма метода опорных векторов), DecisionTreeClassifier, NearestNeighbors или многие другие алгоритмы обучения классификации, реализованные в scikit-learn.
4.4 Особенности алгоритмов обучения
Здесь я описываю некоторые практические особенности, которые могут отличать один алгоритм обучения от другого. Вы уже знаете, что разные алгоритмы обучения могут иметь разные гиперпараметры (\(C\) в SVM, \(\epsilon\) и \(d\) в ID3). Решатели, такие как градиентный спуск, также могут иметь гиперпараметры, например \(\alpha\).
Некоторые алгоритмы, такие как обучение деревьев решений, могут принимать категориальные признаки. Например, если у вас есть признак «цвет», который может принимать значения «красный», «желтый» или «зеленый», вы можете оставить этот признак как есть. SVM, логистическая и линейная регрессия, а также kNN (с метриками косинусного сходства или евклидова расстояния) ожидают числовых значений для всех признаков. Все алгоритмы, реализованные в scikit-learn, ожидают числовых признаков. В следующей главе я покажу, как преобразовывать категориальные признаки в числовые.
Некоторые алгоритмы, такие как SVM, позволяют аналитику данных предоставлять веса для каждого класса. Эти веса влияют на то, как проводится граница принятия решений. Если вес некоторого класса высок, алгоритм обучения старается не делать ошибок при прогнозировании обучающих примеров этого класса (обычно за счет совершения ошибки в другом месте). Это может быть важно, если экземпляры некоторого класса составляют меньшинство в ваших обучающих данных, но вы хотели бы избежать неправильной классификации примеров этого класса как можно больше.
Некоторые модели классификации, такие как SVM и kNN, по заданному вектору признаков выводят только класс. Другие, такие как логистическая регрессия или деревья решений, также могут возвращать оценку от 0 до 1, которую можно интерпретировать либо как уверенность модели в предсказании, либо как вероятность того, что входной пример принадлежит определенному классу4.
Некоторые алгоритмы классификации (например, обучение деревьев решений, логистическая регрессия или SVM) строят модель, используя весь набор данных сразу. Если у вас появились дополнительные размеченные примеры, вам придется
перестраивать модель с нуля. Другие алгоритмы (такие как наивный Байес, многослойный перцептрон, SGDClassifier/SGDRegressor, PassiveAggressiveClassifier/PassiveAggressiveRegressor в scikit-learn) могут обучаться итеративно, по одному пакету за раз. Как только появляются новые обучающие примеры, вы можете обновить модель, используя только новые данные.
Наконец, некоторые алгоритмы, такие как обучение деревьев решений, SVM и kNN, могут использоваться как для классификации, так и для регрессии, в то время как другие могут решать только один тип задач: либо классификацию, либо регрессию, но не обе.
Обычно каждая библиотека предоставляет документацию, которая объясняет, какой тип задач решает каждый алгоритм, какие входные значения допустимы и какой тип вывода производит модель. Документация также предоставляет информацию о гиперпараметрах.
1Как вы знаете, линейная регрессия имеет решение в замкнутой форме. Это означает, что градиентный спуск не нужен для решения этой конкретной задачи. Однако в целях иллюстрации линейная регрессия — идеальная задача для объяснения градиентного спуска.
2В сложных моделях, таких как нейронные сети, которые имеют тысячи параметров, инициализация параметров может существенно повлиять на решение, найденное с помощью градиентного спуска. Существуют различные методы инициализации (случайно, все нули, малые значения около нуля и другие), и это важный выбор, который должен сделать аналитик данных.
3Точка задается текущими значениями параметров.
4Если это действительно необходимо, оценку для предсказаний SVM и kNN можно синтетически создать с помощью простых методов.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения