Глава 6. Нейронные сети и глубокое обучение
Прежде всего, вы уже знаете, что такое нейронная сеть, и вы уже знаете, как построить такую модель. Да, это логистическая регрессия! На самом деле, модель логистической регрессии, а точнее ее обобщение для многоклассовой классификации, называемое моделью регрессии softmax, является стандартным блоком в нейронной сети.
6.1 Нейронные сети
Если вы поняли линейную регрессию, логистическую регрессию и градиентный спуск, понимание нейронных сетей не должно составить проблемы.
Нейронная сеть (neural network - NN), так же как модель регрессии или SVM, является математической функцией:
\[ y = f_{NN}(x). \]Функция \(f_{NN}\) имеет особую форму: это вложенная функция (nested function). Вы, вероятно, уже слышали о слоях (layers) нейронной сети. Так, для 3-слойной нейронной сети, возвращающей скаляр, \(f_{NN}\) выглядит так:
\[ y = f_{NN}(x) = f_3(f_2(f_1(x))). \]В приведенном выше уравнении \(f_1\) и \(f_2\) являются векторными функциями следующего вида:
\[ \mathbf{f}_l(\mathbf{z}) \stackrel{\text{def}}{=} \mathbf{g}_l(\mathbf{W}_l \mathbf{z} + \mathbf{b}_l), \quad (1) \]где \(l\) называется индексом слоя и может изменяться от 1 до любого количества слоев. Функция \(\mathbf{g}_l\) называется функцией активации (activation function). Это фиксированная, обычно нелинейная функция, выбираемая аналитиком данных перед началом обучения. Параметры \(\mathbf{W}_l\) (матрица) и \(\mathbf{b}_l\) (вектор) для каждого слоя изучаются с использованием знакомого градиентного спуска путем оптимизации, в зависимости от задачи, конкретной функции стоимости (например, MSE). Сравните ур. 1 с уравнением для логистической регрессии, где вы заменяете \(\mathbf{g}_l\) сигмоидной функцией, и вы не увидите никакой разницы. Функция \(f_3\) является скалярной функцией для задачи регрессии, но также может быть векторной функцией в зависимости от вашей проблемы.
Вы можете задаться вопросом, почему используется матрица \(\mathbf{W}_l\), а не вектор \(\mathbf{w}_l\). Причина в том, что \(\mathbf{g}_l\) — это векторная функция. Каждая строка \(\mathbf{w}_{l,u}\) (u для блока) матрицы \(\mathbf{W}_l\) является вектором той же размерности, что и \(\mathbf{z}\). Пусть \(a_{l,u} = \mathbf{w}_{l,u}\mathbf{z} + b_{l,u}\). Выход \(\mathbf{f}_l(\mathbf{z})\) — это вектор \([g_l(a_{l,1}), g_l(a_{l,2}), \dots, g_l(a_{l,\text{size}_l})]\), где \(g_l\) — некоторая скалярная функция1, а \(\text{size}_l\) — количество блоков (units) в слое \(l\). Чтобы сделать это более конкретным, давайте рассмотрим одну архитектуру нейронных сетей, называемую многослойным перцептроном (multilayer perceptron) и часто называемую ванильной нейронной сетью (vanilla neural network).
6.1.1 Пример многослойного перцептрона
Мы подробнее рассмотрим одну конкретную конфигурацию нейронных сетей, называемую нейронными сетями прямого распространения (feed-forward neural networks - FFNN), и более конкретно архитектуру, называемую многослойным перцептроном (multilayer perceptron - MLP). В качестве иллюстрации рассмотрим MLP с тремя слоями. Наша сеть принимает двумерный вектор признаков на вход и выводит число. Эта FFNN может быть моделью регрессии или классификации, в зависимости от функции активации, используемой в третьем, выходном слое.
Наш MLP изображен на Рисунке 1 (в pdf). Нейронная сеть представлена графически как связанная комбинация блоков (units), логически организованных в один или несколько слоев (layers). Каждый блок представлен либо кругом, либо прямоугольником. Входящая стрелка представляет вход блока и указывает, откуда пришел этот вход. Исходящая стрелка указывает выход блока.
Выход каждого блока является результатом математической операции, записанной внутри прямоугольника. Круглые блоки ничего не делают с входом; они просто передают свой вход непосредственно на выход.
В каждом прямоугольном блоке происходит следующее. Во-первых, все входы блока объединяются, чтобы сформировать входной вектор. Затем блок применяет линейное преобразование к входному вектору, точно так же, как модель линейной регрессии делает со своим входным вектором признаков. Наконец, блок применяет функцию активации \(g\) к результату линейного преобразования и получает выходное значение, вещественное число. В ванильной FFNN выходное значение блока некоторого слоя становится входным значением каждого из блоков последующего слоя.
На Рисунке 1 функция активации \(g_l\) имеет один индекс: \(l\), индекс слоя, к которому принадлежит блок. Обычно все блоки слоя используют одну и ту же функцию активации, но это не правило. Каждый слой может иметь разное количество блоков. Каждый блок имеет свои параметры \(\mathbf{w}_{l,u}\) и \(b_{l,u}\), где \(u\) — индекс блока, а \(l\) — индекс слоя. Вектор \(\mathbf{y}_{l-1}\) в каждом блоке определяется как \([y_{l-1}^{(1)}, y_{l-1}^{(2)}, y_{l-1}^{(3)}, y_{l-1}^{(4)}]\). Вектор \(\mathbf{x}\) в первом слое определяется как \([x^{(1)}, \dots, x^{(D)}]\). Как вы можете видеть на Рисунке 1, в многослойном перцептроне все выходы одного слоя связаны с каждым входом последующего слоя. Эта архитектура называется полносвязной (fully-connected). Нейронная сеть может содержать полносвязные слои (fully-connected layers). Это слои, блоки которых получают в качестве входов выходы каждого из блоков предыдущего слоя.
6.1.2 Архитектура нейронной сети прямого распространения
Если мы хотим решить задачу регрессии или классификации, рассмотренную в предыдущих главах, последний (крайний правый) слой нейронной сети обычно содержит только один блок. Если функция активации \(g_{last}\) последнего блока линейна, то нейронная сеть является моделью регрессии. Если \(g_{last}\) является логистической функцией, нейронная сеть является моделью бинарной классификации.
Аналитик данных может выбрать любую математическую функцию в качестве \(g_{l,u}\), предполагая, что она дифференцируема2. Последнее свойство необходимо для градиентного спуска, используемого для поиска значений параметров \(\mathbf{w}_{l,u}\) и \(b_{l,u}\) для всех \(l\) и \(u\). Основная цель наличия нелинейных компонентов в функции \(f_{NN}\) — позволить нейронной сети аппроксимировать нелинейные функции. Без нелинейностей \(f_{NN}\) была бы линейной, независимо от того, сколько у нее слоев. Причина в том, что \(\mathbf{W}_l \mathbf{z} + \mathbf{b}_l\) является линейной функцией, а линейная функция от линейной функции также является линейной.
Популярными выборами функций активации являются логистическая функция, уже известная вам, а также TanH и ReLU. Первая — это функция гиперболического тангенса, похожая на логистическую функцию, но изменяющаяся от -1 до 1 (не достигая их). Вторая — это функция выпрямленной линейной единицы (rectified linear unit), которая равна нулю, когда ее вход \(z\) отрицателен, и равна \(z\) в противном случае:
\[ \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}, \] \[ \text{relu}(z) = \begin{cases} 0 & \text{если } z < 0 \\ z & \text{иначе} \end{cases}. \]Как я уже говорил выше, \(\mathbf{W}_l\) в выражении \(\mathbf{W}_l \mathbf{z} + \mathbf{b}_l\) — это матрица, а \(\mathbf{b}_l\) — вектор. Это отличается от \(wz + b\) в линейной регрессии. В матрице \(\mathbf{W}_l\) каждая строка \(u\) соответствует вектору параметров \(\mathbf{w}_{l,u}\). Размерность вектора \(\mathbf{w}_{l,u}\) равна количеству блоков в слое \(l - 1\). Операция \(\mathbf{W}_l \mathbf{z}\) приводит к вектору \(\mathbf{a}_l \stackrel{\text{def}}{=} [\mathbf{w}_{l,1}\mathbf{z}, \mathbf{w}_{l,2}\mathbf{z}, \dots, \mathbf{w}_{l,\text{size}_l}\mathbf{z}]\). Затем сумма \(\mathbf{a}_l + \mathbf{b}_l\) дает \(\text{size}_l\)-мерный вектор \(\mathbf{c}_l\). Наконец, функция \(g_l(\mathbf{c}_l)\) создает вектор \(\mathbf{y}_l \stackrel{\text{def}}{=} [y_l^{(1)}, y_l^{(2)}, \dots, y_l^{(\text{size}_l)}]\) в качестве выхода.
6.2 Глубокое обучение
Глубокое обучение (Deep learning) относится к обучению нейронных сетей с более чем двумя невыходными слоями. В прошлом обучение таких сетей становилось все труднее по мере роста числа слоев. Две самые большие проблемы назывались проблемами взрывающегося градиента (exploding gradient) и исчезающего градиента (vanishing gradient), поскольку для обучения параметров сети использовался градиентный спуск.
Хотя с проблемой взрывающегося градиента было легче справиться, применяя простые методы, такие как отсечение градиента (gradient clipping) и L1 или L2 регуляризация, проблема исчезающего градиента оставалась неразрешимой на протяжении десятилетий.
Что такое исчезающий градиент и почему он возникает? Для обновления значений параметров в нейронных сетях обычно используется алгоритм, называемый обратным распространением ошибки (backpropagation). Обратное распространение ошибки — это эффективный алгоритм для вычисления градиентов в нейронных сетях с использованием правила цепочки. В Главе 4 мы уже видели, как правило цепочки используется для вычисления частных производных сложной функции. Во время градиентного спуска параметры нейронной сети получают
обновление, пропорциональное частной производной функции стоимости по текущему параметру на каждой итерации обучения. Проблема в том, что в некоторых случаях градиент будет исчезающе мал, эффективно предотвращая изменение значения некоторых параметров. В худшем случае это может полностью остановить дальнейшее обучение нейронной сети.
Традиционные функции активации, такие как упомянутая выше функция гиперболического тангенса, имеют градиенты в диапазоне (0, 1), а обратное распространение ошибки вычисляет градиенты по правилу цепочки. Это приводит к умножению \(n\) таких малых чисел для вычисления градиентов более ранних (крайних левых) слоев в \(n\)-слойной сети, что означает, что градиент уменьшается экспоненциально с \(n\). Это приводит к тому, что более ранние слои обучаются очень медленно, если вообще обучаются.
Однако современные реализации алгоритмов обучения нейронных сетей позволяют эффективно обучать очень глубокие нейронные сети (до сотен слоев). Это связано с несколькими улучшениями, объединенными вместе, включая ReLU, LSTM (и другие вентильные блоки; мы рассмотрим их ниже), а также такие методы, как пропускающие соединения (skip connections), используемые в остаточных нейронных сетях (residual neural networks), а также продвинутые модификации алгоритма градиентного спуска.
Поэтому сегодня, поскольку проблемы исчезающего и взрывающегося градиента в основном решены (или их влияние уменьшено) в значительной степени, термин «глубокое обучение» относится к обучению нейронных сетей с использованием современного алгоритмического и математического инструментария независимо от того, насколько глубока нейронная сеть. На практике многие бизнес-задачи могут быть решены с помощью нейронных сетей, имеющих 2-3 слоя между входным и выходным слоями. Слои, которые не являются ни входными, ни выходными, часто называют скрытыми слоями (hidden layers).
6.2.1 Сверточная нейронная сеть
Вы могли заметить, что количество параметров, которое может иметь MLP, растет очень быстро по мере увеличения размера вашей сети. В частности, при добавлении одного слоя вы добавляете \((\text{size}_{l-1} + 1) \cdot \text{size}_l\) параметров (наша матрица \(\mathbf{W}_l\) плюс вектор \(\mathbf{b}_l\)). Это означает, что если вы добавите еще один слой из 1000 блоков к существующей нейронной сети, вы добавите более 1 миллиона дополнительных параметров к вашей модели. Оптимизация таких больших моделей — очень вычислительно интенсивная задача.
Когда наши обучающие примеры — это изображения, вход имеет очень высокую размерность3. Если вы хотите научиться классифицировать изображения с помощью MLP, задача оптимизации, скорее всего, станет неразрешимой.
Сверточная нейронная сеть (convolutional neural network - CNN) — это особый вид FFNN, который значительно уменьшает количество параметров в глубокой нейронной сети с большим количеством блоков, не теряя слишком много в качестве модели. CNN нашли применение в обработке изображений и текста, где они превзошли многие ранее установленные эталоны.
Поскольку CNN были изобретены с учетом обработки изображений, я объясню их на примере классификации изображений.
Вы могли заметить, что на изображениях пиксели, расположенные близко друг к другу, обычно представляют один и тот же тип информации: небо, вода, листья, мех, кирпичи и так далее. Исключение из правила составляют края (edges): части изображения, где два разных объекта «касаются» друг друга.
Если мы сможем обучить нейронную сеть распознавать области с одинаковой информацией, а также края, это знание позволит нейронной сети предсказать объект, представленный на изображении. Например, если нейронная сеть обнаружила несколько областей кожи и края, похожие на части овала с тоном кожи внутри и голубоватым тоном снаружи, то, вероятно, это лицо на фоне неба. Если наша цель — обнаруживать людей на фотографиях, нейронная сеть, скорее всего, преуспеет в предсказании человека на этой картинке.
Имея в виду, что самая важная информация на изображении является локальной, мы можем разделить изображение на квадратные фрагменты (patches), используя подход скользящего окна (moving window)4. Затем мы можем обучить несколько меньших моделей регрессии одновременно, каждая малая модель регрессии получает квадратный фрагмент в качестве входа. Цель каждой малой модели регрессии — научиться обнаруживать определенный тип шаблона (pattern) во входном фрагменте. Например, одна малая модель регрессии научится обнаруживать небо; другая — траву, третья — края здания и так далее.
В CNN малая модель регрессии выглядит как та, что на Рисунке 1, но у нее есть только слой 1 и нет слоев 2 и 3. Чтобы обнаружить какой-то шаблон, малая модель регрессии должна изучить параметры матрицы \(\mathbf{F}\) (от «фильтр») размером \(p \times p\), где \(p\) — размер фрагмента. Предположим, для простоты, что входное изображение черно-белое, где 1 представляет черные пиксели, а 0 — белые. Предположим также, что наши фрагменты имеют размер \(3 \times 3\) пикселя (\(p = 3\)). Некоторый фрагмент может тогда выглядеть как следующая матрица \(\mathbf{P}\) (от «фрагмент»):
\[ \mathbf{P} = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 0 \end{pmatrix}. \]Приведенный выше фрагмент представляет узор, похожий на крест. Малая модель регрессии, которая будет обнаруживать такие узоры (и только их), должна будет изучить матрицу параметров \(\mathbf{F}\) размером \(3 \times 3\), где параметры на позициях, соответствующих 1 во входном фрагменте, будут положительными числами, а параметры на позициях, соответствующих 0, будут близки к нулю. Если мы вычислим свертку (convolution) матриц \(\mathbf{P}\) и \(\mathbf{F}\), полученное значение будет тем выше, чем больше \(\mathbf{F}\) похожа на \(\mathbf{P}\). Чтобы проиллюстрировать свертку двух матриц, предположим, что \(\mathbf{F}\) выглядит так:
\[ \mathbf{F} = \begin{pmatrix} 0 & 2 & 3 \\ 2 & 4 & 1 \\ 0 & 3 & 0 \end{pmatrix}. \]Тогда оператор свертки определен только для матриц, имеющих одинаковое количество строк и столбцов. Для наших матриц \(\mathbf{P}\) и \(\mathbf{F}\) он вычисляется, как показано ниже: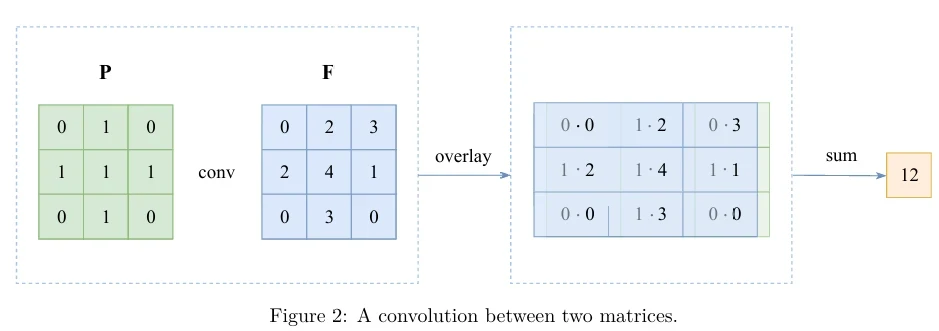
См. Рисунок 2 для визуализации.
Если бы наш входной фрагмент \(\mathbf{P}\) имел другой узор, например, букву L,
\[ \mathbf{P} = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{pmatrix}, \]то свертка с \(\mathbf{F}\) дала бы меньший результат: 5. Таким образом, вы можете видеть, что чем больше фрагмент «похож» на фильтр, тем выше значение операции свертки. Для удобства также существует параметр смещения (bias) \(b\), связанный с каждым фильтром \(\mathbf{F}\), который добавляется к результату свертки перед применением нелинейности (функции активации).
Один слой CNN состоит из нескольких сверточных фильтров (каждый со своим параметром смещения), точно так же, как один слой в ванильной FFNN состоит из нескольких блоков. Каждый фильтр первого (крайнего левого) слоя скользит — или свертывается (convolves) — по входному изображению, слева направо, сверху вниз, и свертка вычисляется на каждой итерации.
Иллюстрация процесса приведена на Рисунке 3 (в pdf), где показаны 6 шагов свертки одного фильтра по изображению.
Матрица фильтра (по одной для каждого фильтра в каждом слое) и значения смещения являются обучаемыми параметрами, которые оптимизируются с помощью градиентного спуска с обратным распространением ошибки.
К сумме свертки и члена смещения применяется нелинейность. Обычно функция активации ReLU используется во всех скрытых слоях. Функция активации выходного слоя зависит от задачи.
Поскольку у нас может быть \(\text{size}_l\) фильтров в каждом слое \(l\), выход сверточного слоя \(l\) будет состоять из \(\text{size}_l\) матриц, по одной для каждого фильтра.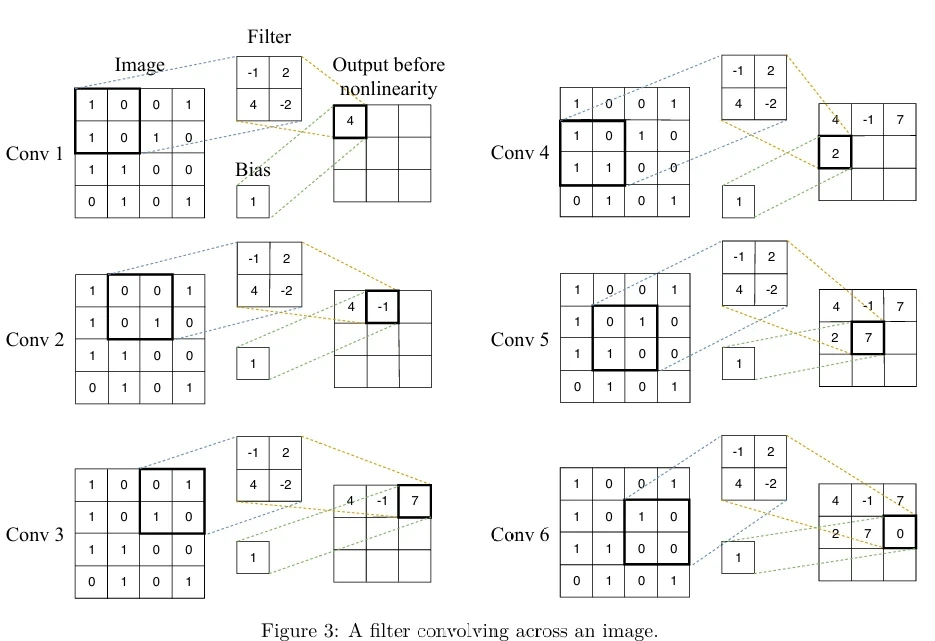
Если в CNN один сверточный слой следует за другим сверточным слоем, то последующий слой \(l + 1\) рассматривает выход предыдущего слоя \(l\) как коллекцию из \(\text{size}_l\) матриц изображений. Такая коллекция называется объемом (volume). Размер этой коллекции называется глубиной объема (volume's depth). Каждый фильтр слоя \(l + 1\) свертывается со всем объемом. Свертка фрагмента объема — это просто сумма сверток соответствующих фрагментов отдельных матриц, из которых состоит объем.
Пример свертки фрагмента объема, состоящего из глубины 3, показан на Рисунке 4 (в pdf). Значение свертки, -3, было получено как \((-2 \cdot 3 + 3 \cdot 1 + 5 \cdot 4 + -1 \cdot 1) + (-2 \cdot 2 + 3 \cdot (-1) + 5 \cdot (-3) + -1 \cdot 1) + (-2 \cdot 1 + 3 \cdot (-1) + 5 \cdot 2 + -1 \cdot (-1)) + (-2)\).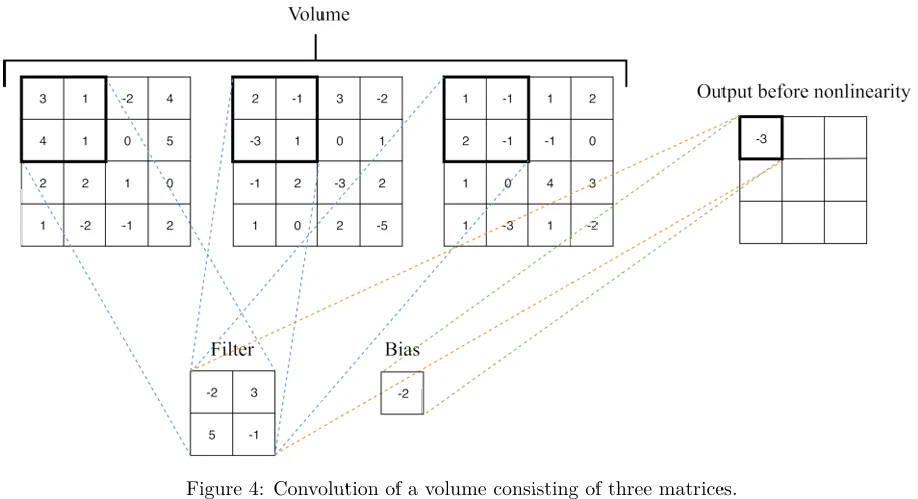
В компьютерном зрении CNN часто получают объемы на вход, поскольку изображение обычно представляется тремя каналами: R, G и B, причем каждый канал является монохромным изображением.
Два важных свойства свертки — это шаг (stride) и дополнение (padding). Шаг — это размер шага скользящего окна. На Рисунке 3 шаг равен 1, то есть фильтр скользит вправо и вниз на одну ячейку за раз. На Рисунке 5 вы можете видеть частичный пример свертки с шагом 2. Вы можете видеть, что выходная матрица меньше, когда шаг больше.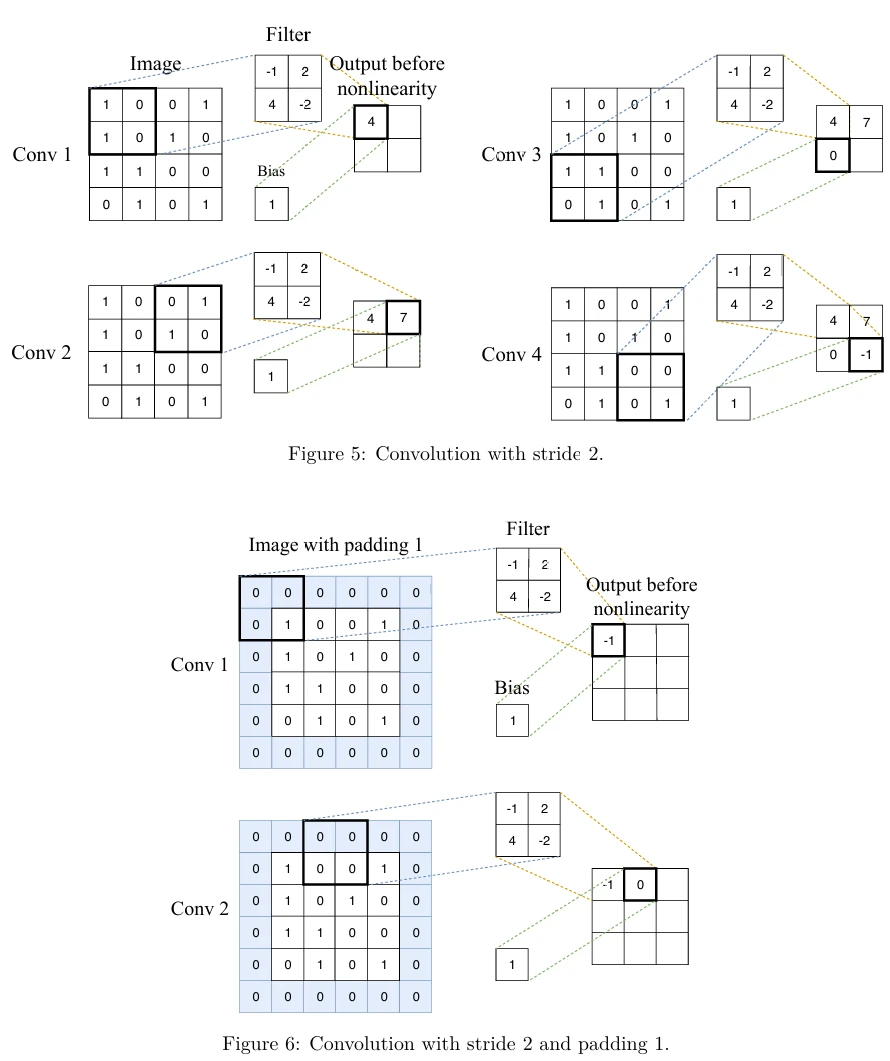
Дополнение позволяет получить большую выходную матрицу; это ширина квадрата дополнительных ячеек, которыми вы окружаете изображение (или объем) перед его сверткой с фильтром. Ячейки, добавленные путем дополнения, обычно содержат нули. На Рисунке 3 дополнение равно 0, поэтому к изображению не добавляются дополнительные ячейки. На Рисунке 6, с другой стороны, шаг равен 2, а дополнение равно 1, поэтому к изображению добавляется квадрат шириной 1 из дополнительных ячеек. Вы можете видеть, что выходная матрица больше, когда дополнение больше5.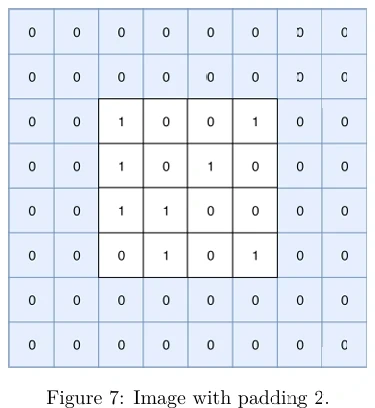
Пример изображения с дополнением 2 показан на Рисунке 7 (в pdf). Дополнение полезно при работе с большими фильтрами, поскольку позволяет им лучше «сканировать» границы изображения.
Этот раздел не был бы полным без представления пулинга (pooling), техники, очень часто используемой в CNN. Пулинг работает очень похоже на свертку, как фильтр, применяемый с использованием подхода скользящего окна. Однако вместо применения обучаемого фильтра к входной матрице или объему, слой пулинга применяет фиксированный оператор, обычно либо максимум (max), либо среднее (average). Аналогично свертке, пулинг имеет гиперпараметры: размер фильтра и шаг. Пример макс-пулинга с фильтром размера 2 и шагом 2 показан на Рисунке 8 .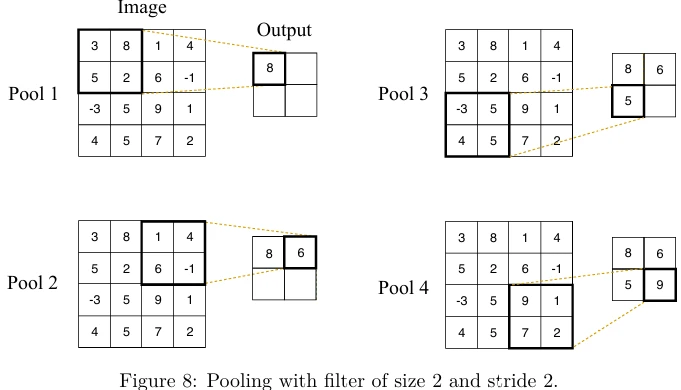
Обычно слой пулинга следует за сверточным слоем и получает выход свертки на вход. Когда пулинг применяется к объему, каждая матрица в объеме обрабатывается независимо от других. Следовательно, выход слоя пулинга, примененного к объему, является объемом той же глубины, что и вход.
Как вы можете видеть, у пулинга есть только гиперпараметры и нет параметров для изучения. Обычно на практике используются фильтры размера 2 или 3 и шаг 2. Макс-пулинг более популярен, чем средний, и часто дает лучшие результаты.
Обычно пулинг способствует повышению точности модели. Он также повышает скорость обучения за счет уменьшения количества параметров нейронной сети. (Как вы можете видеть на Рисунке 8, с фильтром размера 2 и шагом 2 количество параметров уменьшается до 25%, то есть до 4 параметров вместо 16.)
6.2.2 Рекуррентная нейронная сеть
Рекуррентные нейронные сети (recurrent neural networks - RNNs) используются для разметки, классификации или генерации последовательностей (sequences). Последовательность — это матрица, каждая строка которой является вектором признаков, и порядок строк имеет значение. Разметить последовательность — значит предсказать класс для каждого вектора признаков в последовательности. Классифицировать последовательность — значит предсказать класс для всей последовательности. Сгенерировать последовательность — значит вывести другую последовательность (возможно, другой длины), каким-то образом связанную с входной последовательностью.
RNN часто используются в обработке текста, потому что предложения и тексты являются естественными последовательностями либо слов/знаков препинания, либо последовательностями символов. По той же причине рекуррентные нейронные сети также используются в обработке речи.
Рекуррентная нейронная сеть не является сетью прямого распространения: она содержит циклы. Идея заключается в том, что каждый блок \(u\) рекуррентного слоя \(l\) имеет вещественное состояние (state) \(h_{l,u}\). Состояние можно рассматривать как память блока. В RNN каждый блок \(u\) в каждом слое \(l\) получает два входа: вектор состояний из предыдущего слоя \(l - 1\) и вектор состояний из этого же слоя \(l\) с предыдущего временного шага (time step).
Чтобы проиллюстрировать идею, рассмотрим первый и второй рекуррентные слои RNN. Первый (крайний левый) слой получает вектор признаков на вход. Второй слой получает выход первого слоя на вход.
Эта ситуация схематически изображена на Рисунке 9 (в pdf). Как я уже говорил выше, каждый обучающий пример — это матрица, в которой каждая строка является вектором признаков. Для простоты проиллюстрируем эту матрицу как последовательность векторов \(\mathbf{X} = [\mathbf{x}^1, \mathbf{x}^2, \dots, \mathbf{x}^{t-1}, \mathbf{x}^t, \mathbf{x}^{t+1}, \dots, \mathbf{x}^{\text{length}_X}]\), где \(\text{length}_X\) — длина входной последовательности. Если наш входной пример \(\mathbf{X}\) — это текстовое предложение, то вектор признаков \(\mathbf{x}^t\) для каждого \(t = 1, \dots, \text{length}_X\) представляет слово в предложении на позиции \(t\).
Как показано на Рисунке 9, в RNN векторы признаков из входного примера «считываются» нейронной сетью последовательно в порядке временных шагов. Индекс \(t\) обозначает временной шаг. Чтобы обновить состояние \(h_{l,u}^t\) на каждом временном шаге \(t\) в каждом блоке \(u\) каждого слоя \(l\), мы сначала вычисляем линейную комбинацию входного вектора признаков с вектором состояния \(\mathbf{h}_l^{t-1}\) этого же слоя с предыдущего временного шага, \(t - 1\). Линейная комбинация двух векторов вычисляется с использованием двух векторов параметров \(\mathbf{w}_{l,u}\), \(\mathbf{u}_{l,u}\) и параметра \(b_{l,u}\). Значение \(h_{l,u}^t\) затем получается путем применения функции активации \(g_1\) к результату линейной комбинации. Типичным выбором для функции \(g_1\) является \(\tanh\). Выход \(\mathbf{y}_l^t\) обычно является вектором, вычисляемым для всего слоя \(l\) сразу. Чтобы получить \(\mathbf{y}_l^t\), мы используем функцию активации \(g_2\), которая принимает вектор на вход и возвращает другой вектор той же размерности. Функция \(g_2\) применяется к линейной комбинации значений вектора состояния \(\mathbf{h}_l^t\), вычисленных с использованием матрицы параметров \(\mathbf{V}_l\) и вектора параметров \(\mathbf{c}_l\). В классификации типичным выбором для \(g_2\) является функция softmax:
\[ \boldsymbol{\sigma}(\mathbf{z}) \stackrel{\text{def}}{=} [\sigma^{(1)}, \dots, \sigma^{(D)}], \quad \text{где } \sigma^{(j)} \stackrel{\text{def}}{=} \frac{\exp(z^{(j)})}{\sum_{k=1}^D \exp(z^{(k)})}. \]Функция softmax является обобщением сигмоидной функции на многомерные выходы. Она обладает свойством \(\sum_{j=1}^D \sigma^{(j)} = 1\) и \(\sigma^{(j)} > 0\) для всех \(j\).
Размерность \(\mathbf{V}_l\) выбирается аналитиком данных таким образом, чтобы умножение матрицы \(\mathbf{V}_l\) на вектор \(\mathbf{h}_l^t\) приводило к вектору той же размерности, что и вектор \(\mathbf{c}_l\). Этот выбор зависит от размерности выходной метки \(y\) в ваших обучающих данных. (До сих пор мы видели только одномерные метки, но в будущих главах мы увидим, что метки также могут быть многомерными.)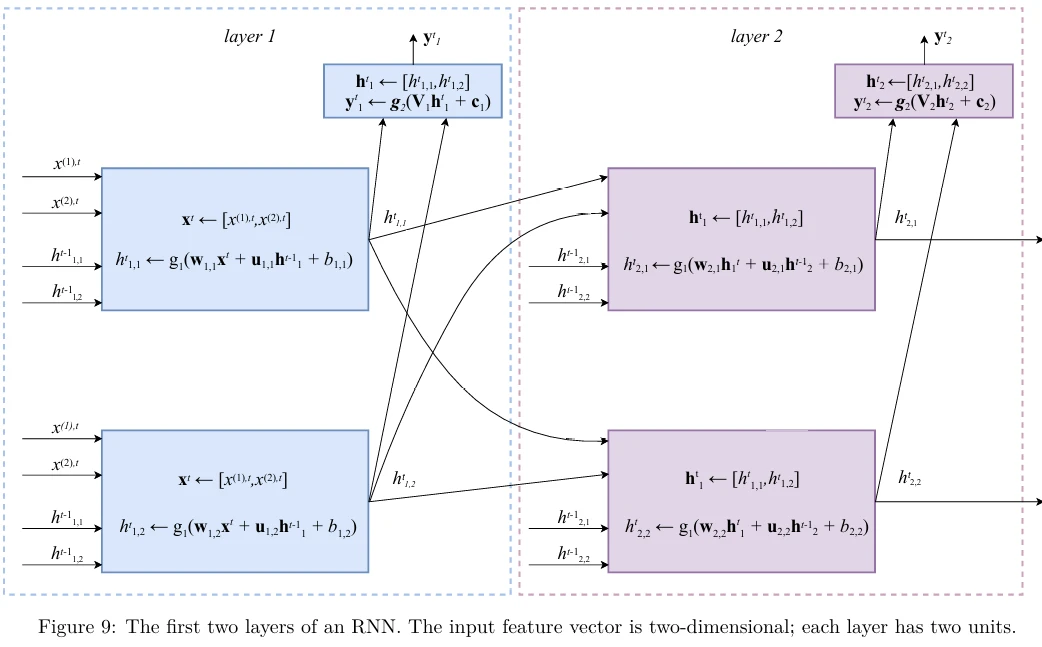
Значения \(\mathbf{w}_{l,u}\), \(\mathbf{u}_{l,u}\), \(b_{l,u}\), \(\mathbf{V}_{l,u}\) и \(\mathbf{c}_l\) вычисляются из обучающих данных с использованием градиентного спуска с обратным распространением ошибки. Для обучения моделей RNN используется специальная версия обратного распространения ошибки, называемая обратным распространением ошибки во времени (backpropagation through time).
И \(\tanh\), и softmax страдают от проблемы исчезающего градиента. Даже если наша RNN имеет всего один или два рекуррентных слоя, из-за последовательной природы входа обратное распространение ошибки должно «развернуть» сеть во времени. С точки зрения вычисления градиента, на практике это означает, что чем длиннее входная последовательность, тем глубже развернутая сеть.
Другая проблема, с которой сталкиваются RNN, — это обработка долгосрочных зависимостей (long-term dependencies). По мере роста длины входной последовательности векторы признаков с начала последовательности имеют тенденцию «забываться», поскольку состояние каждого блока, которое служит памятью сети, становится значительно затронутым векторами признаков, считанными позже. Следовательно, в обработке текста или речи может быть потеряна причинно-следственная связь между далекими словами в длинном предложении.
Наиболее эффективными моделями рекуррентных нейронных сетей, используемыми на практике, являются вентильные RNN (gated RNNs). К ним относятся сети долгой краткосрочной памяти (long short-term memory - LSTM) и сети на основе вентильного рекуррентного блока (gated recurrent unit - GRU).
Прелесть использования вентильных блоков в RNN заключается в том, что такие сети могут хранить информацию в своих блоках для будущего использования, подобно битам в памяти компьютера. Отличие от реальной
памяти заключается в том, что чтение, запись и стирание информации, хранящейся в каждом блоке, контролируются функциями активации, принимающими значения в диапазоне (0, 1). Обученная нейронная сеть может «читать» входную последовательность векторов признаков и решать на некотором раннем временном шаге \(t\) сохранить конкретную информацию о векторах признаков. Эта информация о более ранних векторах признаков может позже использоваться моделью для обработки векторов признаков ближе к концу входной последовательности. Например, если входной текст начинается со слова she, модель RNN для обработки языка может решить сохранить информацию о роде, чтобы правильно интерпретировать слово their, увиденное позже в предложении.
Блоки принимают решения о том, какую информацию хранить, и когда разрешать чтение, запись и стирание. Эти решения изучаются из данных и реализуются через концепцию вентилей (gates). Существует несколько архитектур вентильных блоков. Простой, но эффективной является так называемая минимальная вентильная единица (minimal gated unit), состоящая из ячейки памяти и вентиля забывания.
Давайте рассмотрим математику блока GRU на примере первого слоя RNN (того, который принимает последовательность векторов признаков на вход). Минимальный вентильный блок \(u\) в слое \(l\) принимает два входа: вектор значений ячеек памяти от всех блоков того же слоя с предыдущего временного шага, \(\mathbf{h}_l^{t-1}\), и вектор признаков \(\mathbf{x}^t\). Затем он использует эти два вектора следующим образом (все операции в приведенной ниже последовательности выполняются в блоке одна за другой):
\begin{align*} \tilde{\mathbf{h}}_{l,u}^t &\leftarrow g_1(\mathbf{w}_{l,u} \mathbf{x}^t + \mathbf{u}_{l,u} \mathbf{h}_l^{t-1} + \mathbf{b}_{l,u}), \\ \mathbf{\Gamma}_{l,u}^t &\leftarrow g_2(\mathbf{m}_{l,u} \mathbf{x}^t + \mathbf{o}_{l,u} \mathbf{h}_l^{t-1} + \mathbf{a}_{l,u}), \\ \mathbf{h}_{l,u}^t &\leftarrow \mathbf{\Gamma}_{l,u}^t \tilde{\mathbf{h}}_l^t + (1 - \mathbf{\Gamma}_{l,u}^t) \mathbf{h}_l^{t-1}, \\ \mathbf{h}_l^t &\leftarrow [\mathbf{h}_{l,1}^t, \dots, \mathbf{h}_{l,\text{size}_l}^t] \\ \mathbf{y}_l^t &\leftarrow g_3(\mathbf{V}_l \mathbf{h}_l^t + \mathbf{c}_{l,u}), \end{align*}где \(g_1\) — это функция активации \(\tanh\), \(g_2\) называется функцией вентиля (gate function) и реализуется как сигмоидная функция, принимающая значения в диапазоне (0, 1). Если вентиль \(\mathbf{\Gamma}_{l,u}\) близок к 0, то ячейка памяти сохраняет свое значение с предыдущего временного шага, \(\mathbf{h}_l^{t-1}\). С другой стороны, если вентиль \(\mathbf{\Gamma}_{l,u}\) близок к 1, значение ячейки памяти перезаписывается новым значением \(\tilde{\mathbf{h}}_{l,u}^t\) (см. третье присваивание сверху). Как и в стандартных RNN, \(g_3\) обычно является softmax.
Вентильный блок принимает вход и хранит его некоторое время. Это эквивалентно применению тождественной функции (\(f(x) = x\)) к входу. Поскольку производная тождественной функции постоянна, когда сеть с вентильными блоками обучается с помощью обратного распространения ошибки во времени, градиент не исчезает.
Другие важные расширения RNN включают двунаправленные RNN (bi-directional RNNs), RNN с вниманием (attention) и модели RNN последовательность-в-последовательность (sequence-to-sequence). Последние, в частности, часто используются для построения моделей нейронного машинного перевода и других моделей для преобразования текста в текст. Обобщением RNN является рекурсивная нейронная сеть (recursive neural network).
1Скалярная функция выводит скаляр, то есть простое число, а не вектор.
2Функция должна быть дифференцируема во всей своей области определения или в большинстве точек своей области определения. Например, ReLU не дифференцируема в 0.
3Каждый пиксель изображения является признаком. Если наше изображение имеет размер 100 на 100 пикселей, то у нас 10 000 признаков.
4Рассматривайте это так, как если бы вы смотрели на долларовую купюру под микроскопом. Чтобы увидеть всю купюру, вам нужно постепенно перемещать ее слева направо и сверху вниз. В каждый момент времени вы видите только часть купюры фиксированных размеров. Этот подход называется скользящим окном.
5Для экономии места на Рисунке 6 показаны только первые две из девяти сверток.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения