Глава 7. Задачи и решения
7.1 Ядерная регрессия
Мы говорили о линейной регрессии, но что, если наши данные не имеют формы прямой линии? Может помочь полиномиальная регрессия. Допустим, у нас есть одномерные данные \({(x_i, y_i)}_{i=1}^N\). Мы могли бы попытаться подогнать квадратичную линию \(y = w_1 x_i + w_2 x_i^2 + b\) к нашим данным. Определив функцию стоимости среднеквадратичной ошибки (MSE), мы могли бы применить градиентный спуск и найти значения параметров \(w_1, w_2\) и \(b\), которые минимизируют эту функцию стоимости. В одномерном или двумерном пространстве мы можем легко увидеть, подходит ли функция к данным. Однако, если наш вход — это \(D\)-мерный вектор признаков, с \(D > 3\), найти правильный полином будет сложно.
Ядерная регрессия (Kernel regression) — это непараметрический метод. Это означает, что нет параметров для изучения. Модель основана на самих данных (как в kNN). В своей простейшей форме в ядерной регрессии мы ищем модель вида:
\[ f(x) = \frac{1}{N} \sum_{i=1}^N w_i y_i, \quad \text{где } w_i = \frac{N k\left(\frac{x_i - x}{b}\right)}{\sum_{l=1}^N k\left(\frac{x_l - x}{b}\right)}. \quad (1) \]Функция \(k(\cdot)\) называется ядром (kernel). Ядро играет роль функции сходства: значения коэффициентов \(w_i\) выше, когда \(x\) похож на \(x_i\), и ниже, когда они непохожи. Ядра могут иметь разные формы, наиболее часто используемое — гауссово ядро:
\[ k(z) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right). \]
Если ваши входы — многомерные векторы признаков, члены \(x_i - x\) и \(x_l - x\) в ур. 1 должны быть заменены евклидовым расстоянием \(\|x_i - x\|\) и \(\|x_l - x\|\) соответственно.
Значение \(b\) является гиперпараметром, который мы настраиваем с использованием валидационного набора (путем запуска модели, построенной с конкретным значением \(b\), на примерах валидационного набора и вычисления MSE). Вы можете видеть иллюстрацию влияния \(b\) на форму линии регрессии на Рисунке 1 (в pdf).
7.2 Многоклассовая классификация
Хотя многие задачи классификации могут быть определены с использованием двух классов, некоторые определяются с более чем двумя классами, что требует адаптации наших алгоритмов машинного обучения.
При многоклассовой классификации (multiclass classification) метка может быть одним из \(C\) классов: \(y \in \{1, \dots, C\}\). Многие алгоритмы машинного обучения являются бинарными; SVM — пример. Некоторые алгоритмы могут быть естественным образом расширены для обработки многоклассовых задач. ID3 и другие алгоритмы обучения деревьев решений можно просто изменить следующим образом:
\[ f^{\mathcal{S}}_{ID3} \stackrel{\text{def}}{=} \text{Pr}(y_i = c|x) = \frac{1}{|\mathcal{S}|} \sum_{\{y | (x,y) \in \mathcal{S}, y=c\}} y, \]для всех \(c \in \{1, \dots, C\}\), где \(\mathcal{S}\) — листовой узел, в котором делается предсказание.
Логистическая регрессия может быть естественным образом расширена на задачи многоклассового обучения путем замены сигмоидной функции функцией softmax, которую мы уже видели в Главе 6.
Алгоритм kNN также просто расширяется на многоклассовый случай: когда мы находим \(k\) ближайших примеров для входа \(x\) и изучаем их, мы возвращаем класс, который мы видели чаще всего среди \(k\) примеров.
SVM не может быть естественным образом расширен на многоклассовые задачи. Другие алгоритмы могут быть реализованы более эффективно в бинарном случае. Что делать, если у вас многоклассовая задача, но бинарный алгоритм обучения классификации? Одна из распространенных стратегий называется один против остальных (one versus rest). Идея состоит в том, чтобы преобразовать многоклассовую задачу в \(C\) бинарных задач классификации и построить \(C\) бинарных классификаторов. Например, если у нас три класса, \(y \in \{1, 2, 3\}\), мы создаем копии исходных наборов данных и изменяем их. В первой копии мы заменяем все метки, не равные 1, на 0. Во второй копии мы заменяем все метки, не равные 2, на 0. В третьей копии мы заменяем все метки, не равные 3, на 0. Теперь у нас есть три задачи бинарной классификации, где нам нужно научиться различать метки 1 и 0, 2 и 0, и 3 и 0.
Как только у нас есть три модели, чтобы классифицировать новый входной вектор признаков \(x\), мы применяем три модели к входу и получаем три предсказания. Затем мы выбираем предсказание ненулевого класса, которое является наиболее уверенным (certain). Помните, что в логистической регрессии модель возвращает не метку, а оценку (между 0 и 1), которую можно интерпретировать как вероятность того, что метка положительна. Мы также можем интерпретировать эту оценку как уверенность предсказания. В SVM аналогом уверенности является расстояние \(d\) от входа \(x\) до границы принятия решений, заданное,
\[ d \stackrel{\text{def}}{=} \frac{|\mathbf{w}^* \mathbf{x} + b^*|}{\|\mathbf{w}\|}. \]Чем больше расстояние, тем увереннее предсказание. Большинство алгоритмов обучения либо могут быть естественным образом преобразованы в многоклассовый случай, либо они возвращают оценку, которую мы можем использовать в стратегии «один против остальных».
7.3 Одноклассовая классификация
Иногда у нас есть только примеры одного класса, и мы хотим обучить модель, которая отличала бы примеры этого класса от всего остального.
Одноклассовая классификация (One-class classification), также известная как унарная классификация (unary classification) или моделирование класса (class modeling), пытается идентифицировать объекты определенного класса среди всех объектов, обучаясь на обучающем наборе, содержащем только объекты этого класса. Это отличается от и сложнее, чем традиционная задача классификации, которая пытается различить два или более классов с обучающим набором, содержащим объекты из всех классов. Типичной задачей одноклассовой классификации является классификация трафика в защищенной компьютерной сети как нормального. В этом сценарии мало, если вообще есть, примеров трафика во время атаки или вторжения. Однако примеров нормального трафика часто в избытке. Алгоритмы обучения одноклассовой классификации используются для обнаружения выбросов (outlier detection), обнаружения аномалий (anomaly detection) и обнаружения новизны (novelty detection).
Существует несколько алгоритмов обучения одного класса. Наиболее широко используемые на практике — одноклассовый гауссовский (one-class Gaussian), одноклассовый k-средних (one-class k-means), одноклассовый kNN (one-class kNN) и одноклассовый SVM (one-class SVM).
Идея одноклассового гауссовского метода заключается в том, что мы моделируем наши данные так, как если бы они были получены из гауссовского распределения, точнее, многомерного нормального распределения (multivariate normal distribution - MND). Функция плотности вероятности (pdf) для MND задается следующим уравнением:
\[ f_{\boldsymbol{\mu},\boldsymbol{\Sigma}}(\mathbf{x}) = \frac{\exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)}{\sqrt{(2\pi)^D |\boldsymbol{\Sigma}|}}, \]где \(f_{\boldsymbol{\mu},\boldsymbol{\Sigma}}(\mathbf{x})\) возвращает плотность вероятности, соответствующую входному вектору признаков \(\mathbf{x}\). Плотность вероятности можно интерпретировать как правдоподобие того, что пример \(\mathbf{x}\) был взят из распределения вероятностей, которое мы моделируем как MND. Значения \(\boldsymbol{\mu}\) (вектор) и \(\boldsymbol{\Sigma}\) (матрица) являются параметрами, которые мы должны изучить. Критерий максимального правдоподобия (аналогично тому, как мы решали задачу обучения логистической регрессии) оптимизируется для нахождения оптимальных значений этих двух параметров. \(|\boldsymbol{\Sigma}| \stackrel{\text{def}}{=} \det \boldsymbol{\Sigma}\) — это определитель (determinant) матрицы \(\boldsymbol{\Sigma}\); обозначение \(\boldsymbol{\Sigma}^{-1}\) означает обратную матрицу (inverse) матрицы \(\boldsymbol{\Sigma}\).
Если термины определитель и обратная матрица для вас новы, не волнуйтесь. Это стандартные операции над векторами и матрицами из раздела математики, называемого теорией матриц. Если вы чувствуете необходимость узнать, что это такое, Википедия хорошо объясняет эти понятия.
На практике числа в векторе \(\boldsymbol{\mu}\) определяют место, где центрирована кривая нашего гауссовского распределения, в то время как числа в \(\boldsymbol{\Sigma}\) определяют форму кривой. Для обучающего набора, состоящего из двумерных векторов признаков, пример одноклассовой гауссовской модели приведен на Рисунке 2 .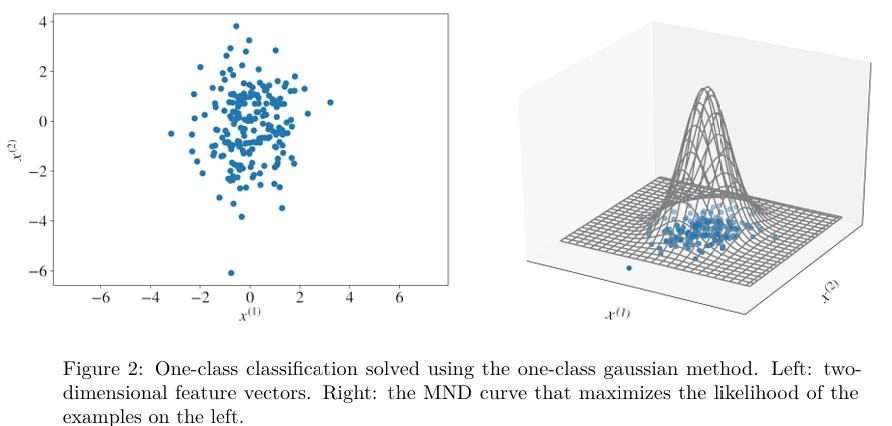
Как только у нас есть наша модель, параметризованная \(\boldsymbol{\mu}\) и \(\boldsymbol{\Sigma}\), изученными из данных, мы предсказываем правдоподобие каждого входа \(\mathbf{x}\), используя \(f_{\boldsymbol{\mu},\boldsymbol{\Sigma}}(\mathbf{x})\). Только если правдоподобие выше определенного порога, мы предсказываем, что пример принадлежит нашему классу; в противном случае он классифицируется как выброс. Значение порога находится экспериментально или с использованием «обоснованного предположения».
Когда данные имеют более сложную форму, более продвинутый алгоритм может использовать комбинацию нескольких гауссиан (называемую смесью гауссиан (mixture of Gaussians)). В этом случае для изучения из данных требуется больше параметров: по одному \(\boldsymbol{\mu}\) и \(\boldsymbol{\Sigma}\) для каждой гауссианы, а также параметры, позволяющие комбинировать несколько гауссиан для формирования одной pdf. В Главе 9 мы рассмотрим смесь гауссиан применительно к кластеризации.
Одноклассовый k-средних и одноклассовый kNN основаны на аналогичном принципе, что и одноклассовый гауссовский: построить некоторую модель данных, а затем определить порог, чтобы решить, похож ли наш новый вектор признаков на другие примеры согласно модели. В первом случае все обучающие примеры кластеризуются с использованием алгоритма кластеризации k-средних, и, когда наблюдается новый пример \(\mathbf{x}\), вычисляется расстояние \(d(\mathbf{x})\) как минимальное расстояние между \(\mathbf{x}\) и центром каждого кластера. Если \(d(\mathbf{x})\) меньше определенного порога, то \(\mathbf{x}\) принадлежит классу.
Одноклассовый SVM, в зависимости от формулировки, пытается либо 1) отделить все обучающие примеры от начала координат (в пространстве признаков) и максимизировать расстояние от гиперплоскости до начала координат, либо 2) получить сферическую границу вокруг данных путем минимизации объема этой гиперсферы. Я оставляю описание алгоритма одноклассового kNN, а также
детали одноклассового k-средних и одноклассового SVM для дополнительного чтения.
7.4 Многометочночная классификация
В некоторых ситуациях для описания примера из набора данных подходит более одной метки. В этом случае мы говорим о многометочной классификации (multi-label classification).
Например, если мы хотим описать изображение, мы могли бы присвоить ему несколько меток: «хвойное дерево», «гора», «дорога», все три одновременно (Рисунок 3 ).
Если количество возможных значений для меток велико, но все они одного типа, например, теги, мы можем преобразовать каждый размеченный пример в несколько размеченных примеров, по одному на метку. Эти новые примеры все имеют одинаковый вектор признаков и только одну метку. Это становится задачей многоклассовой классификации. Мы можем решить ее, используя стратегию «один против остальных». Единственное отличие от обычной многоклассовой задачи заключается в том, что теперь у нас есть новый гиперпараметр: порог (threshold). Если оценка предсказания для некоторой метки выше порога, эта метка предсказывается для входного вектора признаков. В этом сценарии для одного вектора признаков может быть предсказано несколько меток. Значение порога выбирается с использованием валидационного набора.
Аналогично, алгоритмы, которые естественным образом могут быть сделаны многоклассовыми (деревья решений, логистическая регрессия и нейронные сети среди прочих), могут быть применены к задачам многометочной классификации. Поскольку они возвращают оценку для каждого класса, мы можем определить порог и затем присвоить несколько меток одному вектору признаков, если оценка выше порога.
Алгоритмы нейронных сетей могут естественным образом обучать модели многометочной классификации, используя
функцию стоимости бинарной перекрестной энтропии (binary cross-entropy). Выходной слой нейронной сети в этом случае имеет по одному блоку на метку. Каждый блок выходного слоя имеет сигмоидную функцию активации. Соответственно, каждая метка \(l\) является бинарной (\(y_{i,l} \in \{0, 1\}\)), где \(l = 1, \dots, L\) и \(i = 1, \dots, N\). Бинарная перекрестная энтропия предсказания вероятности \(\hat{y}_{i,l}\), что пример \(x_i\) имеет метку \(l\), определяется как,
\[ -(y_{i,l} \ln(\hat{y}_{i,l}) + (1 - y_{i,l}) \ln(1 - \hat{y}_{i,l})). \]Критерий минимизации — это просто среднее значение всех членов бинарной перекрестной энтропии по всем обучающим примерам и всем меткам этих примеров.
В случаях, когда количество возможных значений, которые может принимать каждая метка, невелико, можно преобразовать многометочную задачу в многоклассовую, используя другой подход. Представьте себе следующую проблему. Мы хотим размечать изображения, и метки могут быть двух типов. Первый тип метки может иметь два возможных значения: {фото, картина}; метка второго типа может иметь три возможных значения {портрет, пейзаж, другое}. Мы можем создать новый поддельный класс для каждой комбинации двух исходных классов, например:
| Поддельный Класс | Реальный Класс 1 | Реальный Класс 2 |
|---|---|---|
| 1 | фото | портрет |
| 2 | фото | пейзаж |
| 3 | фото | другое |
| 4 | картина | портрет |
| 5 | картина | пейзаж |
| 6 | картина | другое |
Теперь у нас есть те же размеченные примеры, но мы заменяем реальные мултиметки одной поддельной меткой со значениями от 1 до 6. Этот подход хорошо работает на практике, когда возможных комбинаций классов не слишком много. В противном случае вам потребуется гораздо больше обучающих данных для компенсации увеличенного набора классов.
Основное преимущество последнего подхода заключается в том, что вы сохраняете корреляцию ваших меток, в отличие от ранее рассмотренных методов, которые предсказывают каждую метку независимо от других. Корреляция между метками может быть важна во многих задачах. Например, если вы хотите предсказать, является ли электронное письмо спамом или не_спамом, одновременно предсказывая, является ли оно обычным или приоритетным. Вы хотели бы избежать предсказаний типа [спам, приоритетное].
7.5 Ансамблевое обучение
Фундаментальные алгоритмы, которые мы рассмотрели в Главе 3, имеют свои ограничения. Из-за своей простоты они иногда не могут создать достаточно точную модель для вашей проблемы. Вы могли бы попробовать использовать глубокие нейронные сети. Однако на практике глубокие нейронные сети требуют
значительного количества размеченных данных, которых у вас может не быть. Другой подход к повышению производительности простых алгоритмов обучения — это ансамблевое обучение (ensemble learning).
Ансамблевое обучение — это парадигма обучения, которая вместо того, чтобы пытаться обучить одну сверxточную модель, фокусируется на обучении большого количества моделей с низкой точностью, а затем комбинировании предсказаний, данных этими слабыми моделями (weak models), для получения метамодели (meta-model) с высокой точностью.
Модели с низкой точностью обычно изучаются слабыми учениками (weak learners), то есть алгоритмами обучения, которые не могут изучать сложные модели и, следовательно, обычно быстры во время обучения и предсказания. Наиболее часто используемым слабым учеником является алгоритм обучения деревьев решений, в котором мы часто останавливаем разделение обучающего набора всего после нескольких итераций. Полученные деревья неглубокие и не особенно точные, но идея ансамблевого обучения заключается в том, что если деревья не идентичны и каждое дерево хотя бы немного лучше случайного угадывания, то мы можем получить высокую точность, комбинируя большое количество таких деревьев.
Для получения предсказания для входа \(x\) предсказания каждой слабой модели комбинируются с использованием некоторого вида взвешенного голосования (weighted voting). Конкретная форма взвешивания голосов зависит от алгоритма, но, независимо от алгоритма, идея та же: если совет слабых моделей предсказывает, что сообщение является спамом, то мы присваиваем метку спам \(x\).
Два основных метода ансамблевого обучения — это бустинг (boosting) и бэггинг (bagging).
7.5.1 Бустинг и Бэггинг
Бустинг заключается в использовании исходных обучающих данных и итеративном создании нескольких моделей с помощью слабого ученика. Каждая новая модель будет отличаться от предыдущих в том смысле, что слабый ученик, строя каждую новую модель, пытается «исправить» ошибки, допущенные предыдущими моделями. Окончательная ансамблевая модель представляет собой определенную комбинацию этих нескольких слабых моделей, построенных итеративно.
Бэггинг заключается в создании множества «копий» обучающих данных (каждая копия немного отличается от другой), а затем применении слабого ученика к каждой копии для получения нескольких слабых моделей и их последующего комбинирования. Широко используемый и эффективный алгоритм машинного обучения, основанный на идее бэггинга, — это случайный лес (random forest).
7.5.2 Случайный лес
«Ванильный» алгоритм бэггинга работает следующим образом. Имея обучающий набор, мы создаем \(B\) случайных выборок \(\mathcal{S}_b\) (для каждого \(b = 1, \dots, B\)) обучающего набора и строим модель дерева решений \(f_b\), используя каждую выборку \(\mathcal{S}_b\) в качестве обучающего набора. Для выборки \(\mathcal{S}_b\) для некоторого \(b\) мы делаем выборку с возвращением (sampling with replacement). Это означает, что мы начинаем с пустого множества, а затем выбираем случайным образом пример из обучающего набора и помещаем его точную копию в \(\mathcal{S}_b\), сохраняя исходный пример в исходном обучающем наборе. Мы продолжаем выбирать примеры случайным образом, пока \(|\mathcal{S}_b| = N\).
После обучения у нас есть \(B\) деревьев решений. Предсказание для нового примера \(x\) получается как среднее значение \(B\) предсказаний:
\[ y \leftarrow \hat{f}(x) \stackrel{\text{def}}{=} \frac{1}{B} \sum_{b=1}^B f_b(x), \]в случае регрессии, или путем принятия решения большинством голосов в случае классификации.
Случайный лес отличается от ванильного бэггинга только одним способом. Он использует модифицированный алгоритм обучения деревьев, который проверяет на каждом разбиении в процессе обучения случайное подмножество признаков. Причина этого — избежать корреляции деревьев: если один или несколько признаков являются очень сильными предикторами для целевой переменной, эти признаки будут выбраны для разбиения примеров во многих деревьях. Это приведет ко многим коррелированным деревьям в нашем «лесу». Коррелированные предикторы не могут помочь в улучшении точности предсказания. Основная причина лучшей производительности ансамблирования моделей заключается в том, что модели, которые хороши, скорее всего, сойдутся на одном и том же предсказании, в то время как плохие модели, скорее всего, разойдутся в разных. Корреляция заставит плохие модели чаще сходиться, что помешает голосованию большинством или усреднению.
Наиболее важными гиперпараметрами для настройки являются количество деревьев, \(B\), и размер случайного подмножества признаков для рассмотрения на каждом разбиении.
Случайный лес — один из наиболее широко используемых алгоритмов ансамблевого обучения. Почему он так эффективен? Причина в том, что, используя несколько выборок исходного набора данных, мы уменьшаем дисперсию окончательной модели. Помните, что низкая дисперсия означает низкое переобучение. Переобучение происходит, когда наша модель пытается объяснить малые вариации в наборе данных, потому что наш набор данных — это всего лишь малая выборка из популяции всех возможных примеров явления, которое мы пытаемся смоделировать. Если нам не повезло с тем, как был выбран наш обучающий набор, он может содержать некоторые нежелательные (но неизбежные) артефакты: шум, выбросы и пере- или недопредставленные примеры. Создавая несколько случайных выборок с возвращением нашего обучающего набора, мы уменьшаем влияние этих артефактов.
7.5.3 Градиентный бустинг
Другой эффективный алгоритм ансамблевого обучения, основанный на идее бустинга, — это градиентный бустинг (gradient boosting). Давайте сначала рассмотрим градиентный бустинг для регрессии. Чтобы построить сильный регрессор, мы начинаем с постоянной модели \(f = f_0\) (как мы делали в ID3):
\[ f = f_0(x) \stackrel{\text{def}}{=} \frac{1}{N} \sum_{i=1}^N y_i. \]Затем мы изменяем метки каждого примера \(i = 1, \dots, N\) в нашем обучающем наборе следующим образом:
\[ \hat{y}_i \leftarrow y_i - f(x_i), \quad (2) \]где \(\hat{y}_i\), называемый остатком (residual), является новой меткой для примера \(x_i\).
Теперь мы используем модифицированный обучающий набор с остатками вместо исходных меток, чтобы построить новую модель дерева решений, \(f_1\). Модель бустинга теперь определяется как \(f \stackrel{\text{def}}{=} f_0 + \alpha f_1\), где \(\alpha\) — скорость обучения (гиперпараметр).
Затем мы пересчитываем остатки, используя ур. 2, и снова заменяем метки в обучающих данных, обучаем новую модель дерева решений \(f_2\), переопределяем модель бустинга как \(f \stackrel{\text{def}}{=} f_0 + \alpha f_1 + \alpha f_2\), и процесс продолжается до тех пор, пока не будет объединено предопределенное максимальное количество деревьев \(M\).
Интуитивно, что здесь происходит? Вычисляя остатки, мы выясняем, насколько хорошо (или плохо) целевая переменная каждого обучающего примера предсказывается текущей моделью \(f\). Затем мы обучаем другое дерево, чтобы исправить ошибки текущей модели (вот почему мы используем остатки вместо реальных меток), и добавляем это новое дерево к существующей модели с некоторым весом \(\alpha\). Следовательно, каждое дополнительное дерево, добавленное к модели, частично исправляет ошибки, допущенные предыдущими деревьями, до тех пор, пока не будет достигнуто максимальное количество деревьев \(M\) (другой гиперпараметр).
Теперь вы должны резонно спросить, почему алгоритм называется градиентным бустингом? В градиентном бустинге мы не вычисляем никакого градиента, в отличие от того, что мы делали в Главе 4 для линейной регрессии. Чтобы увидеть сходство между градиентным бустингом и градиентным спуском, вспомните, почему мы вычисляли градиент в линейной регрессии: мы делали это, чтобы получить представление о том, куда нам следует двигать значения наших параметров, чтобы функция стоимости MSE достигла своего минимума. Градиент показывал направление, но мы не знали, как далеко нам следует идти в этом направлении, поэтому мы использовали малый шаг \(\alpha\) на каждой итерации, а затем переоценивали наше направление. То же самое происходит и в градиентном бустинге. Однако вместо того, чтобы получать градиент напрямую, мы используем его прокси в виде остатков: они показывают нам, как нужно скорректировать модель, чтобы ошибка (остаток) уменьшилась.
Три основных гиперпараметра для настройки в градиентном бустинге — это количество деревьев, скорость обучения и глубина деревьев — все три влияют на точность модели. Глубина деревьев также влияет на скорость обучения и предсказания: чем короче, тем быстрее.
Можно показать, что обучение на остатках оптимизирует общую модель \(f\) по критерию среднеквадратичной ошибки. Вы можете видеть разницу с бэггингом здесь: бустинг уменьшает смещение (или недообучение) вместо дисперсии. Как таковой, бустинг может переобучаться. Однако путем настройки глубины и количества деревьев переобучение можно в значительной степени избежать.
Градиентный бустинг для классификации похож, но шаги немного другие. Рассмотрим бинарный случай. Предположим, у нас есть \(M\) регрессионных деревьев решений. Аналогично логистической регрессии, предсказание ансамбля деревьев решений моделируется с использованием сигмоидной функции:
\[ \text{Pr}(y = 1|x, f) \stackrel{\text{def}}{=} \frac{1}{1 + e^{-f(x)}}, \]где \(f(x) \stackrel{\text{def}}{=} \sum_{m=1}^M f_m(x)\), а \(f_m\) — регрессионное дерево.
Опять же, как и в логистической регрессии, мы применяем принцип максимального правдоподобия, пытаясь найти такое \(f\), которое максимизирует \(L_f = \sum_{i=1}^N \ln[\text{Pr}(y_i = 1|x_i, f)]\). Опять же, чтобы избежать числового переполнения, мы максимизируем сумму логарифмов правдоподобия, а не произведение правдоподобий.
Алгоритм начинается с начальной постоянной модели \(f = f_0 = \ln\frac{p}{1-p}\), где \(p = \frac{1}{N}\sum_{i=1}^N y_i\). (Можно показать, что такая инициализация оптимальна для сигмоидной функции.) Затем на каждой итерации \(m\) к модели добавляется новое дерево \(f_m\). Чтобы найти наилучшее \(f_m\), сначала вычисляется частная производная \(g_i\) текущей модели для каждого \(i = 1, \dots, N\):
\[ g_i = \frac{d L_f}{d f}, \]где \(f\) — ансамблевая модель классификатора, построенная на предыдущей итерации \(m - 1\). Чтобы вычислить \(g_i\), нам нужно найти производные \(\ln[\text{Pr}(y_i = 1|x_i, f)]\) по \(f\) для всех \(i\). Обратите внимание, что \(\ln[\text{Pr}(y_i = 1|x_i, f)] \stackrel{\text{def}}{=} \ln\left(\frac{1}{1+e^{-f(x_i)}}\right)\). Производная правой части уравнения по \(f\) равна \(\frac{1}{e^{f(x_i)}+1}\).
Затем мы преобразуем наш обучающий набор, заменяя исходную метку \(y_i\) соответствующей частной производной \(g_i\), и строим новое дерево \(f_m\), используя преобразованный обучающий набор. Затем мы находим оптимальный шаг обновления \(\rho_m\) как:
\[ \rho_m \leftarrow \arg \max_{\rho} L_{f+\rho f_m}. \]В конце итерации \(m\) мы обновляем ансамблевую модель \(f\), добавляя новое дерево \(f_m\):
\[ f \leftarrow f + \alpha \rho_m f_m. \]Мы итерируем до \(m = M\), затем останавливаемся и возвращаем ансамблевую модель \(f\).
Градиентный бустинг — один из самых мощных алгоритмов машинного обучения — не только потому, что он создает очень точные модели, но и потому, что он способен обрабатывать огромные наборы данных с миллионами примеров и признаков. Он обычно превосходит случайный лес по точности, но из-за своей последовательной природы может быть значительно медленнее в обучении.
7.6 Обучение разметке последовательностей
Последовательность — один из наиболее часто встречающихся типов структурированных данных. Мы общаемся, используя последовательности слов и предложений, мы выполняем задачи последовательно, наши гены, музыка, которую мы слушаем, и видео, которые мы смотрим, наши наблюдения за непрерывным процессом, таким как движущийся автомобиль или цена акции, — все это последовательности.
Разметка последовательности (Sequence labeling) — это задача автоматического присвоения метки каждому элементу последовательности. Размеченный последовательный обучающий пример при разметке последовательности — это пара списков \((\mathbf{X}, \mathbf{Y})\),
где \(\mathbf{X}\) — это список векторов признаков, по одному на временной шаг, \(\mathbf{Y}\) — это список меток той же длины. Например, \(\mathbf{X}\) может представлять слова в предложении, такие как [«большая», «красивая», «машина»], а \(\mathbf{Y}\) — список соответствующих частей речи, таких как [«прилагательное», «прилагательное», «существительное»]). Более формально, в примере \(i\), \(\mathbf{X}_i = [\mathbf{x}_i^{(1)}, \mathbf{x}_i^{(2)}, \dots, \mathbf{x}_i^{(\text{size}_i)}]\), где \(\text{size}_i\) — длина последовательности примера \(i\), \(\mathbf{Y}_i = [y_i^{(1)}, y_i^{(2)}, \dots, y_i^{(\text{size}_i)}]\) и \(y_i \in \{1, 2, \dots, C\}\).
Вы уже видели, что RNN можно использовать для разметки последовательности. На каждом временном шаге \(t\) она считывает входной вектор признаков \(\mathbf{x}_i^{(t)}\), и последний рекуррентный слой выводит метку \(y_{last}^{(t)}\) (в случае бинарной разметки) или \(\mathbf{y}_{last}^{(t)}\) (в случае многоклассовой или многометочной разметки).
Однако RNN — не единственная возможная модель для разметки последовательности. Модель под названием Условные случайные поля (Conditional Random Fields - CRF) является очень эффективной альтернативой, которая часто хорошо работает на практике для векторов признаков с большим количеством информативных признаков. Например, представьте, что у нас есть задача извлечения именованных сущностей (named entity extraction), и мы хотим построить модель, которая размечала бы каждое слово в предложении, таком как «Я еду в Сан-Франциско», одним из следующих классов: {местоположение, имя, название_компании, другое}. Если наши векторы признаков (которые представляют слова) содержат такие бинарные признаки, как «начинается ли слово с заглавной буквы» и «можно ли найти слово в списке местоположений», такие признаки были бы очень информативными и помогли бы классифицировать слова Сан и Франциско как местоположение.
Создание признаков вручную, как известно, является трудоемким процессом, требующим значительного уровня знаний в предметной области.
CRF — интересная модель, которую можно рассматривать как обобщение логистической регрессии на последовательности. Однако на практике для задач разметки последовательности ее превзошли двунаправленные глубокие вентильные RNN. CRF также значительно медленнее в обучении, что затрудняет их применение к большим обучающим наборам (с сотнями тысяч примеров). Кроме того, большой обучающий набор — это то, где процветает глубокая нейронная сеть.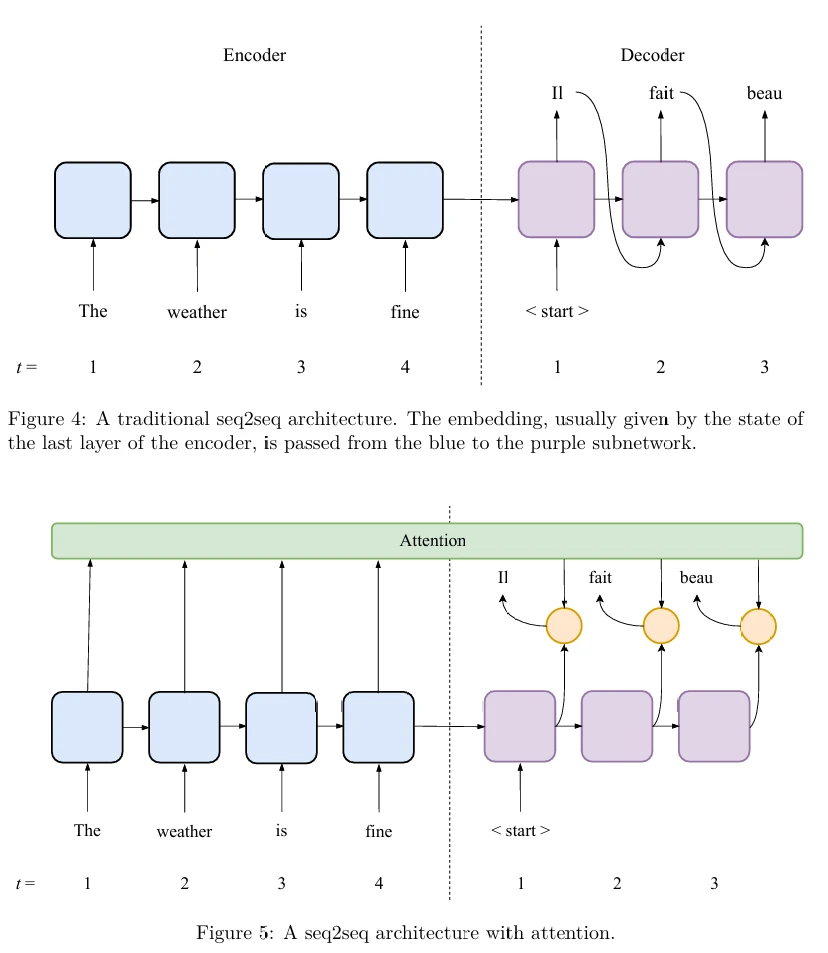
7.7 Обучение Последовательность-в-Последовательность
Обучение Последовательность-в-Последовательность (Sequence-to-sequence learning) (часто сокращаемое как seq2seq learning) — это обобщение задачи разметки последовательности. В seq2seq \(\mathbf{X}_i\) и \(\mathbf{Y}_i\) могут иметь разную длину. Модели seq2seq нашли применение в машинном переводе (где, например, вход — это английское предложение, а выход — соответствующее французское предложение), диалоговых интерфейсах (где вход — это вопрос, набранный пользователем, а выход — ответ от машины), реферировании текста, исправлении орфографии и многих других.
Многие, но не все задачи обучения seq2seq в настоящее время лучше всего решаются с помощью нейронных сетей. Архитектуры сетей, используемые в seq2seq, все имеют две части: кодировщик (encoder) и декодер (decoder).
В обучении нейронных сетей seq2seq кодировщик — это нейронная сеть, которая принимает последовательный вход. Это может быть RNN, но также CNN или какая-то другая архитектура. Роль кодировщика — прочитать вход и сгенерировать некоторое состояние (похожее на состояние в RNN), которое можно рассматривать как числовое представление смысла (meaning) входа, с которым может работать машина. Смысл некоторой сущности, будь то изображение, текст или видео, обычно является вектором или матрицей, содержащей вещественные числа. В жаргоне машинного обучения этот вектор (или матрица) называется вложением (embedding) входа.
Декодер — это другая нейронная сеть, которая принимает вложение на вход и способна генерировать последовательность выходов. Как вы уже могли догадаться, это вложение поступает от кодировщика. Чтобы произвести последовательность выходов, декодер принимает входной вектор признаков начала последовательности (start of sequence) \(\mathbf{x}^{(0)}\) (обычно все нули), производит первый выход \(\mathbf{y}^{(1)}\), обновляет свое состояние, комбинируя вложение и вход \(\mathbf{x}^{(0)}\), а затем использует выход \(\mathbf{y}^{(1)}\) в качестве своего следующего входа \(\mathbf{x}^{(1)}\). Для простоты размерность \(\mathbf{y}^{(t)}\) может быть такой же, как у \(\mathbf{x}^{(t)}\); однако это не строго необходимо. Как мы видели в Главе 6, каждый слой RNN может производить много одновременных выходов: один можно использовать для генерации метки \(\mathbf{y}^{(t)}\), а другой, другой размерности, — в качестве \(\mathbf{x}^{(t)}\).
И кодировщик, и декодер обучаются одновременно, используя обучающие данные. Ошибки на выходе декодера распространяются на кодировщик через обратное распространение ошибки.
Традиционная архитектура seq2seq иллюстрируется на Рисунке 4 (в pdf). Более точные предсказания могут быть получены с использованием архитектуры с вниманием (attention). Механизм внимания реализуется дополнительным набором параметров, которые комбинируют некоторую информацию от кодировщика (в RNN эта информация — список векторов состояния последнего рекуррентного слоя со всех временных шагов кодировщика) и текущее состояние декодера для генерации метки. Это позволяет еще лучше сохранять долгосрочные зависимости, чем это обеспечивается вентильными блоками и двунаправленными RNN.
Архитектура seq2seq с вниманием иллюстрируется на Рисунке 5 (в pdf).
Обучение seq2seq — относительно новая область исследований. Новые архитектуры сетей регулярно открываются и публикуются. Обучение таких архитектур может быть сложным, так как количество
гиперпараметров для настройки и других архитектурных решений может быть ошеломляющим. Обратитесь к вики книги за материалами по последним достижениям, руководствами и примерами кода.
7.8 Активное обучение
Активное обучение (Active learning) — интересная парадигма обучения с учителем. Обычно она применяется, когда получение размеченных примеров является дорогостоящим. Это часто бывает в медицинской или финансовой сферах, где может потребоваться мнение эксперта для аннотирования данных пациентов или клиентов. Идея заключается в том, чтобы начать обучение с относительно небольшого количества размеченных примеров и большого количества неразмеченных, а затем размечать только те примеры, которые вносят наибольший вклад в качество модели.
Существует множество стратегий активного обучения. Здесь мы обсуждаем только следующие две:
- на основе плотности данных и неопределенности, и
- на основе опорных векторов.
Первая стратегия применяет текущую модель \(f\), обученную с использованием существующих размеченных примеров, к каждому из оставшихся неразмеченных примеров (или, чтобы сэкономить время вычислений, к некоторой случайной выборке из них). Для каждого неразмеченного примера \(x\) вычисляется следующая оценка важности: \(\text{density}(x) \cdot \text{uncertainty}_f(x)\). Плотность отражает, сколько примеров окружает \(x\) в его близком соседстве, в то время как \(\text{uncertainty}_f(x)\) отражает, насколько неопределенным является предсказание модели \(f\) для \(x\). В бинарной классификации с сигмоидом, чем ближе оценка предсказания к 0.5, тем более неопределенным является предсказание. В SVM, чем ближе пример к границе принятия решений, тем более неопределенным является предсказание.
В многоклассовой классификации в качестве типичной меры неопределенности можно использовать энтропию:
\[ H_f(x) = - \sum_{c=1}^C \text{Pr}(y^{(c)}; f(x)) \ln[\text{Pr}(y^{(c)}; f(x))], \]где \(\text{Pr}(y^{(c)}; f(x))\) — это оценка вероятности, которую модель \(f\) присваивает классу \(y^{(c)}\) при классификации \(x\). Вы можете видеть, что если для каждого \(y^{(c)}\), \(f(y^{(c)}) = \frac{1}{C}\), то модель наиболее неопределенна, и энтропия максимальна и равна 1; с другой стороны, если для некоторого \(y^{(c)}\), \(f(y^{(c)}) = 1\), то модель уверена в классе \(y^{(c)}\), и энтропия минимальна и равна 0.
Плотность для примера \(x\) можно получить, взяв среднее значение расстояния от \(x\) до каждого из его \(k\) ближайших соседей (где \(k\) — гиперпараметр).
Как только мы узнаем оценку важности каждого неразмеченного примера, мы выбираем тот, у которого самая высокая оценка важности, и просим эксперта его аннотировать. Затем мы добавляем новый аннотированный пример в обучающий набор, перестраиваем модель и продолжаем процесс до тех пор, пока не будет удовлетворен некоторый критерий остановки. Критерий остановки может быть выбран заранее (например, максимальное количество запросов к эксперту на основе доступного бюджета) или зависеть от того, насколько хорошо работает наша модель согласно некоторой метрике.
Стратегия активного обучения на основе опорных векторов заключается в построении модели SVM с использованием размеченных данных. Затем мы просим нашего эксперта аннотировать неразмеченный пример, который лежит ближе всего к гиперплоскости, разделяющей два класса. Идея заключается в том, что если пример лежит ближе всего к гиперплоскости, то он наименее определен и внесет наибольший вклад в уменьшение возможных мест, где может лежать истинная (та, которую мы ищем) гиперплоскость.
Некоторые стратегии активного обучения могут учитывать стоимость запроса метки у эксперта. Другие учатся спрашивать мнение эксперта. Стратегия «запрос комитетом» заключается в обучении нескольких моделей с использованием разных методов, а затем запросе у эксперта разметки примера, по которому эти модели расходятся во мнениях больше всего. Некоторые стратегии пытаются выбрать примеры для разметки таким образом, чтобы уменьшить дисперсию или смещение модели.
7.9 Полуавтоматическое обучение
При полуавтоматическом обучении (semi-supervised learning - SSL) у нас также размечена малая часть набора данных; большинство оставшихся примеров не размечены. Наша цель — использовать большое количество неразмеченных примеров для улучшения производительности модели, не запрашивая дополнительных размеченных примеров.
Исторически было предпринято множество попыток решить эту проблему. Ни одна из них не могла быть названа общепризнанной и часто используемой на практике. Например, один часто цитируемый метод SSL называется самообучением (self-learning). В самообучении мы используем алгоритм обучения для построения начальной модели с использованием размеченных примеров. Затем мы применяем модель ко всем неразмеченным примерам и размечаем их с помощью модели. Если оценка уверенности предсказания для некоторого неразмеченного примера \(x\) выше некоторого порога (выбранного экспериментально), то мы добавляем этот размеченный пример в наш обучающий набор, переобучаем модель и продолжаем так до тех пор, пока не будет удовлетворен критерий остановки. Мы могли бы остановиться, например, если точность модели не улучшилась в течение последних \(m\) итераций.
Приведенный выше метод может принести некоторое улучшение модели по сравнению с использованием только изначально размеченного набора данных, но увеличение производительности обычно не впечатляет. Более того, на практике качество модели может даже ухудшиться. Это зависит от свойств статистического распределения, из которого были взяты данные, что обычно неизвестно.
С другой стороны, недавние достижения в обучении нейронных сетей принесли некоторые впечатляющие результаты. Например, было показано, что для некоторых наборов данных, таких как MNIST (частый тестовый стенд в компьютерном зрении, состоящий из размеченных изображений рукописных цифр от 0 до 9), модель, обученная полуавтоматическим способом, имеет почти идеальную производительность всего с 10 размеченными примерами на класс (всего 100 размеченных примеров). Для сравнения, MNIST содержит 70 000 размеченных примеров (60 000 для обучения и 10 000 для теста). Архитектура нейронной сети, достигшая такой замечательной производительности, называется лестничной сетью (ladder network). Чтобы понять лестничные сети, вы должны понять, что такое автокодировщик (autoencoder).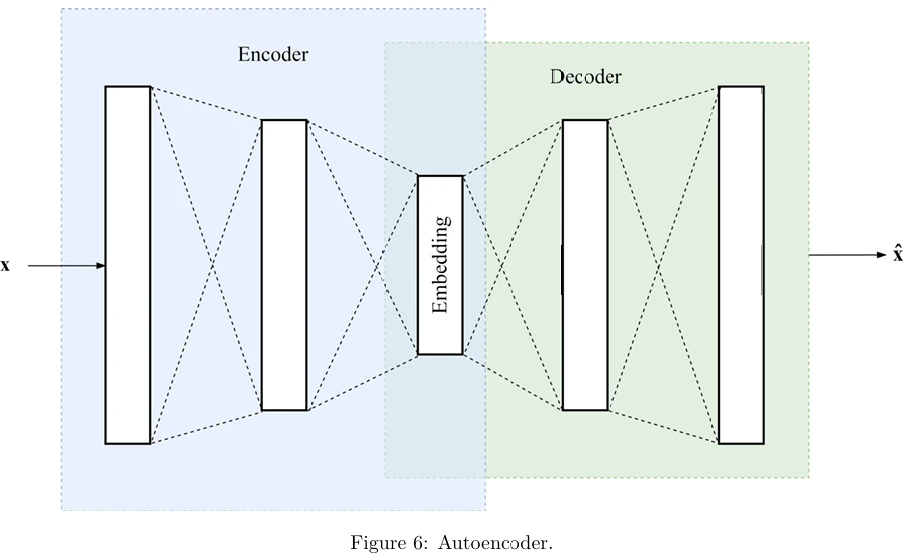
Автокодировщик — это нейронная сеть прямого распространения с архитектурой кодировщик-декодер. Он обучается реконструировать свой вход. Таким образом, обучающий пример — это пара \((\mathbf{x}, \mathbf{x})\). Мы хотим, чтобы выход \(\hat{\mathbf{x}}\) модели \(f(\mathbf{x})\) был как можно более похож на вход \(\mathbf{x}\).
Важная деталь здесь заключается в том, что сеть автокодировщика похожа на песочные часы с узким местом (bottleneck layer) посередине, которое содержит вложение \(D\)-мерного входного вектора; слой вложения обычно имеет гораздо меньше блоков, чем \(D\). Цель декодера — реконструировать входной вектор признаков из этого вложения. Теоретически достаточно иметь 10 блоков в слое узкого места для успешного кодирования изображений MNIST. В типичном автокодировщике, схематично изображенном на Рисунке 6 (в pdf), функция стоимости обычно является либо среднеквадратичной ошибкой (когда признаки могут быть любым числом), либо бинарной перекрестной энтропией (когда признаки бинарны, а блоки последнего слоя декодера имеют сигмоидную функцию активации). Если стоимость — это среднеквадратичная ошибка, то она задается:
\[ \frac{1}{N} \sum_{i=1}^N \|\mathbf{x}_i - f(\mathbf{x}_i)\|^2, \]где \(\|\mathbf{x}_i - f(\mathbf{x}_i)\|\) — евклидово расстояние между двумя векторами.
Шумоподавляющий автокодировщик (denoising autoencoder) искажает левую часть \(\mathbf{x}\) в обучающем примере \((\mathbf{x}, \mathbf{x})\), добавляя некоторую случайную пертурбацию к признакам. Если наши примеры — это изображения в оттенках серого с пикселями, представленными значениями от 0 до 1, обычно к каждому признаку добавляется гауссовский шум. Для каждого признака \(j\) входного вектора признаков \(\mathbf{x}\) значение шума \(n^{(j)}\) выбирается из гауссовского распределения:
\[ n^{(j)} \sim \mathcal{N}(\mu, \sigma^2), \]где обозначение \(\sim\) означает «выбрано из», а \(\mathcal{N}(\mu, \sigma^2)\) обозначает гауссовское распределение со средним \(\mu\) и стандартным отклонением \(\sigma\), pdf которого задается:
\[ f_{\theta}(z) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(z - \mu)^2}{2\sigma^2}\right). \]В приведенном выше уравнении \(\pi\) — константа, а \(\theta \stackrel{\text{def}}{=} [\mu, \sigma]\) — гиперпараметр. Новое, искаженное значение признака \(x^{(j)}\) задается как \(x^{(j)} + n^{(j)}\).
Лестничная сеть — это шумоподавляющий автокодировщик с обновлением. Кодировщик и декодер имеют одинаковое количество слоев. Слой узкого места используется непосредственно для предсказания метки (с использованием функции активации softmax). Сеть имеет несколько функций стоимости. Для каждого слоя \(l\) кодировщика и соответствующего слоя \(l\) декодера одна стоимость \(C_d^l\) штрафует разницу между выходами двух слоев (используя квадрат евклидова расстояния). Когда во время обучения используется размеченный пример, другая функция стоимости, \(C_c\), штрафует ошибку предсказания метки (используется функция стоимости отрицательного логарифма правдоподобия). Комбинированная функция стоимости, \(C_c + \sum_{l=1}^L \lambda_l C_d^l\) (усредненная по всем примерам в пакете), оптимизируется с помощью мини-пакетного стохастического градиентного спуска с обратным распространением ошибки. Гиперпараметры \(\lambda_l\) для каждого слоя \(l\) определяют компромисс между стоимостью классификации и стоимостью кодирования-декодирования.
В лестничной сети не только вход искажается шумом, но и выход каждого слоя кодировщика (во время обучения). Когда мы применяем обученную модель к новому входу \(x\) для предсказания его метки, мы не искажаем вход.
Существуют и другие техники полуавтоматического обучения, не связанные с обучением нейронных сетей. Одна из них подразумевает построение модели с использованием размеченных данных, а затем кластеризацию неразмеченных и размеченных примеров вместе с использованием любой техники кластеризации (мы рассмотрим некоторые из них в Главе 9). Для каждого нового примера мы затем выводим в качестве предсказания метку большинства в кластере, к которому он принадлежит.
Другая техника, называемая S3VM, основана на использовании SVM. Мы строим одну модель SVM для каждой возможной разметки неразмеченных примеров, а затем выбираем модель с наибольшим зазором. Статья по S3VM описывает подход, который позволяет решить эту проблему без фактического перечисления всех возможных разметок.
7.10 Обучение с одного примера (One-Shot Learning)
Эта глава была бы неполной без упоминания двух других важных парадигм обучения с учителем. Одна из них — обучение с одного примера (one-shot learning). В обучении с одного примера, обычно применяемом при распознавании лиц, мы хотим построить модель, которая может распознать, что две фотографии одного и того же человека представляют одного и того же человека. Если мы представим модели две фотографии двух разных людей, мы ожидаем, что модель распознает, что эти два человека разные.
Чтобы решить такую проблему, мы могли бы пойти традиционным путем и построить бинарный классификатор, который принимает два изображения на вход и предсказывает либо истину (когда два изображения представляют одного и того же человека), либо ложь (когда два изображения принадлежат разным людям). Однако на практике это привело бы к нейронной сети, вдвое большей, чем типичная нейронная сеть, потому что каждое из двух изображений нуждается в своей собственной подсети для вложения. Обучение такой сети было бы сложным не только из-за ее размера, но и потому, что положительные примеры было бы гораздо труднее получить, чем отрицательные. Таким образом, проблема сильно несбалансирована.
Один из способов эффективно решить проблему — обучить сиамскую нейронную сеть (siamese neural network - SNN). SNN может быть реализована как любой тип нейронной сети, CNN, RNN или MLP. Сеть принимает только одно изображение на вход за раз; таким образом, размер сети не удваивается. Чтобы получить бинарный классификатор «тот_же_человек»/«не_тот_же» из сети, которая принимает только одно изображение на вход, мы обучаем сети особым образом.
Для обучения SNN мы используем тройную функцию потерь (triplet loss function). Например, пусть у нас есть три изображения лица: изображение A (для якоря), изображение P (для положительного) и изображение N (для отрицательного). A и P — это две разные фотографии одного и того же человека; N — это фотография другого человека. Каждый обучающий пример \(i\) теперь является тройкой \((A_i, P_i, N_i)\).
Допустим, у нас есть модель нейронной сети \(f\), которая может принимать на вход фотографию лица и выводить вложение этой фотографии. Тройная потеря для примера \(i\) определяется как,
\[ \max(\|\mathbf{f}(A_i) - \mathbf{f}(P_i)\|^2 - \|\mathbf{f}(A_i) - \mathbf{f}(N_i)\|^2 + \alpha, 0). \quad (3) \]Функция стоимости определяется как средняя тройная потеря:
\[ \frac{1}{N} \sum_{i=1}^N \max(\|\mathbf{f}(A_i) - \mathbf{f}(P_i)\|^2 - \|\mathbf{f}(A_i) - \mathbf{f}(N_i)\|^2 + \alpha, 0), \]где \(\alpha\) — положительный гиперпараметр. Интуитивно, \(\|\mathbf{f}(A) - \mathbf{f}(P)\|^2\) мало, когда наша нейронная сеть выводит похожие векторы вложения для A и P; \(\|\mathbf{f}(A_i) - \mathbf{f}(N_i)\|^2\) велико, когда вложение для фотографий двух разных людей разное. Если наша модель работает так, как мы хотим, то член \(m = \|\mathbf{f}(A_i) - \mathbf{f}(P_i)\|^2 - \|\mathbf{f}(A_i) - \mathbf{f}(N_i)\|^2\) всегда будет отрицательным, потому что мы вычитаем большое значение из малого. Устанавливая \(\alpha\) выше, мы заставляем член \(m\) быть еще меньше, чтобы убедиться, что модель научилась распознавать два одинаковых лица
и два разных лица с большим зазором. Если \(m\) недостаточно мало, то из-за \(\alpha\) стоимость будет положительной, и параметры модели будут скорректированы при обратном распространении ошибки.
Вместо случайного выбора изображения для N, лучший способ создать тройки для обучения — использовать текущую модель после нескольких эпох обучения и найти кандидатов для N, которые похожи на A и P согласно этой модели. Использование случайных примеров в качестве N значительно замедлило бы обучение, потому что нейронная сеть легко увидит разницу между фотографиями двух случайных людей, поэтому средняя тройная потеря будет низкой большую часть времени, и параметры не будут обновляться достаточно быстро.
Чтобы построить SNN, мы сначала решаем архитектуру нашей нейронной сети. Например, CNN является типичным выбором, если наши входы — изображения. Для данного примера, чтобы вычислить среднюю тройную потерю, мы применяем, последовательно, модель к A, затем к P, затем к N, а затем вычисляем потерю для этого примера, используя ур. 3. Мы повторяем это для всех троек в пакете, а затем вычисляем стоимость; градиентный спуск с обратным распространением ошибки распространяет стоимость через сеть для обновления ее параметров.
Распространенное заблуждение заключается в том, что для обучения с одного примера нам нужен только один пример каждой сущности для обучения. На практике нам нужно более одного примера каждого человека, чтобы модель идентификации личности была точной. Это называется обучением с одного примера из-за наиболее частого применения такой модели: аутентификации на основе лица. Например, такая модель может использоваться для разблокировки вашего телефона. Если ваша модель хороша, то вам нужно иметь только одну фотографию себя на телефоне, и она распознает вас, а также распознает, что кто-то другой — это не вы. Когда у нас есть модель, чтобы решить, принадлежат ли две фотографии A и \(\hat{A}\) одному и тому же человеку, мы проверяем, меньше ли \(\|\mathbf{f}(A) - \mathbf{f}(\hat{A})\|^2\), чем \(\tau\), гиперпараметр.
7.11 Обучение с нуля (Zero-Shot Learning)
Я заканчиваю эту главу обучением с нуля (zero-shot learning). Это относительно новая область исследований, поэтому пока нет алгоритмов, доказавших свою значительную практическую полезность. Поэтому я лишь кратко изложу здесь основную идею и оставлю детали различных алгоритмов для дальнейшего чтения. В обучении с нуля (ZSL) мы хотим обучить модель присваивать метки объектам. Наиболее частое применение — научиться присваивать метки изображениям.
Однако, в отличие от стандартной классификации, мы хотим, чтобы модель могла предсказывать метки, которых у нас не было в обучающих данных. Как это возможно?
Хитрость заключается в использовании вложений не только для представления входа \(x\), но и для представления выхода \(y\). Представьте, что у нас есть модель, которая для любого слова в английском языке может сгенерировать вектор вложения со следующим свойством: если слово \(y_i\) имеет схожее значение со словом \(y_k\), то векторы вложения для этих двух слов будут похожи. Например, если \(y_i\) — Париж, а \(y_k\) — Рим, то у них будут похожие вложения; с другой стороны, если \(y_k\) — картофель, то вложения \(y_i\) и \(y_k\) будут непохожими. Такие векторы вложения называются вложениями слов (word embeddings), и их обычно сравнивают с использованием метрик косинусного сходства1.
Вложения слов обладают таким свойством, что каждое измерение вложения представляет конкретный признак значения слова. Например, если наше вложение слова имеет четыре измерения (обычно они намного шире, от 50 до 300 измерений), то эти четыре измерения могут представлять такие признаки значения, как животность, абстрактность, кислотность и желтизна (да, звучит забавно, но это просто пример). Таким образом, слово пчела имело бы вложение типа [1, 0, 0, 1], слово желтый — типа [0, 1, 0, 1], слово единорог — типа [1, 1, 0, 0]. Значения для каждого вложения получаются с использованием специальной процедуры обучения, применяемой к обширному текстовому корпусу.
Теперь, в нашей задаче классификации, мы можем заменить метку \(y_i\) для каждого примера \(i\) в нашем обучающем наборе ее вложением слова и обучить модель многометочной классификации, которая предсказывает вложения слов. Чтобы получить метку для нового примера \(x\), мы применяем нашу модель \(f\) к \(x\), получаем вложение \(\hat{\mathbf{y}}\) и затем ищем среди всех английских слов те, чьи вложения наиболее похожи на \(\hat{\mathbf{y}}\), используя косинусное сходство.
Почему это работает? Возьмем, к примеру, зебру. Она белая, млекопитающее и имеет полосы. Возьмем рыбу-клоуна: она оранжевая, не млекопитающее и имеет полосы. Теперь возьмем тигра: он оранжевый, имеет полосы и является млекопитающим. Если эти три признака присутствуют во вложениях слов, CNN научится обнаруживать эти же признаки на картинках. Даже если метка тигр отсутствовала в обучающих данных, но присутствовали другие объекты, включая зебр и рыб-клоунов, то CNN, скорее всего, изучит понятия млекопитающее, оранжевость и полосатость для предсказания меток этих объектов. Как только мы представим модели изображение тигра, эти признаки будут правильно идентифицированы на изображении, и, скорее всего, ближайшее вложение слова из нашего английского словаря к предсказанному вложению будет именно у слова тигр.
1 Я покажу в Главе 10, как изучать вложения слов из данных.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- Машинное обучение с помощью Python
- Математика для нейронного обучения