Глава 4. Обработка числовых данных
4.0 Введение
Количественные данные — это измерение чего-либо — будь то размер класса, ежемесячные продажи или оценки студентов. Естественный способ представления этих величин — числовой (например, 29 студентов, 529 392 доллара продаж). В этой главе мы рассмотрим многочисленные стратегии преобразования необработанных числовых данных в признаки, специально созданные для алгоритмов машинного обучения.
4.1 Изменение масштаба признака
Проблема
Вам нужно изменить масштаб значений числового признака, чтобы они находились между двумя значениями.
Решение
Используйте MinMaxScaler scikit-learn для изменения масштаба массива признаков:
# Load libraries
import numpy as np
from sklearn import preprocessing
# Create feature
feature = np.array([[-500.5],
[-100.1],
[0],
[100.1],
[900.9]])
# Create scaler
minmax_scale = preprocessing.MinMaxScaler(feature_range=(0, 1))
# Scale feature
scaled_feature = minmax_scale.fit_transform(feature)
# Show feature
scaled_featurearray([[ 0. ],
[ 0.28571429],
[ 0.35714286],
[ 0.42857143],
[ 1. ]])Обсуждение
Изменение масштаба — распространенная задача предварительной обработки в машинном обучении. Многие алгоритмы, описанные далее в этой книге, будут предполагать, что все признаки имеют одинаковый масштаб, обычно от 0 до 1 или от –1 до 1. Существует несколько методов изменения масштаба, но один из самых простых называется min-max масштабированием. Min-max масштабирование использует минимальное и максимальное значения признака для изменения масштаба значений в пределах диапазона. В частности, min-max вычисляет:
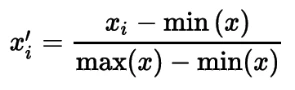
Рисунок: Формула min-max масштабирования
где x — вектор признаков, xi — отдельный элемент признака x, а x'i — масштабированный элемент. В нашем примере мы видим из выведенного массива, что признак успешно масштабирован в диапазоне от 0 до 1:
array([[ 0. ],
[ 0.28571429],
[ 0.35714286],
[ 0.42857143],
[ 1. ]])MinMaxScaler scikit-learn предлагает два варианта масштабирования признака. Один вариант — использовать fit для вычисления минимального и максимального значений признака, а затем использовать transform для масштабирования признака. Второй вариант — использовать fit_transform для выполнения обеих операций одновременно. Между двумя вариантами нет математической разницы, но иногда есть практическая польза в сохранении операций разделенными, поскольку это позволяет применять одно и то же преобразование к разным наборам данных.
См. также
Feature scaling, Wikipedia
About Feature Scaling and Normalization, Sebastian Raschka
4.2 Стандартизация признака
Проблема
Вы хотите преобразовать признак, чтобы он имел среднее значение 0 и стандартное отклонение 1.
Решение
StandardScaler scikit-learn выполняет оба преобразования:
import numpy as np
from sklearn import preprocessing
# Create feature
x = np.array([[-1000.1],
[-200.2],
[500.5],
[600.6],
[9000.9]])
# Create scaler
scaler = preprocessing.StandardScaler()
# Transform the feature
standardized = scaler.fit_transform(x)
# Show feature
standardizedarray([[-0.76058269],
[-0.54177196],
[-0.35009716],
[-0.32271504],
[ 1.97516685]])Обсуждение
Распространенной альтернативой масштабированию min-max, рассмотренному в Рецепте 4.1, является изменение масштаба признаков, чтобы они были приблизительно стандартно нормально распределены. Для достижения этого мы используем стандартизацию для преобразования данных таким образом, чтобы они имели среднее значение, x̄, равное 0, и стандартное отклонение, σ, равное 1. В частности, каждый элемент в признаке преобразуется следующим образом:
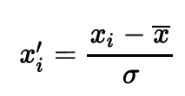
Рисунок: Формула стандартизации
где x'i — наша стандартизованная форма xi. Преобразованный признак представляет собой количество стандартных отклонений, на которое исходное значение отклоняется от среднего значения признака (также называемое z-оценкой в статистике).
Стандартизация — это распространенный метод масштабирования для предварительной обработки в машинном обучении, и по моему опыту он используется чаще, чем масштабирование min-max. Однако это зависит от алгоритма обучения. Например, анализ главных компонент часто работает лучше при использовании стандартизации, тогда как масштабирование min-max часто рекомендуется для нейронных сетей (оба алгоритма обсуждаются далее в этой книге). Как правило, я рекомендую по умолчанию использовать стандартизацию, если у вас нет конкретной причины использовать альтернативу.
Мы можем увидеть эффект стандартизации, взглянув на среднее и стандартное отклонение нашего решения:
# Print mean and standard deviation
print("Mean:", round(standardized.mean()))
print("Standard deviation:", standardized.std())Mean: 0.0
Standard deviation: 1.0Если в наших данных есть значительные выбросы, это может негативно повлиять на нашу стандартизацию, влияя на среднее и дисперсию признака. В этом сценарии часто полезно вместо этого изменить масштаб признака, используя медиану и межквартильный размах. В scikit-learn мы делаем это с помощью метода RobustScaler:
# Create scaler
robust_scaler = preprocessing.RobustScaler()
# Transform feature
robust_scaler.fit_transform(x)array([[ -1.87387612],
[ -0.875 ],
[ 0. ],
[ 0.125 ],
[ 10.61488511]])4.3 Нормализация наблюдений
Проблема
Вы хотите изменить масштаб значений признаков наблюдений, чтобы они имели единичную норму (общая длина равна 1).
Решение
Используйте Normalizer с аргументом norm:
# Load libraries
import numpy as np
from sklearn.preprocessing import Normalizer
# Create feature matrix
features = np.array([[0.5, 0.5],
[1.1, 3.4],
[1.5, 20.2],
[1.63, 34.4],
[10.9, 3.3]])
# Create normalizer
normalizer = Normalizer(norm="l2")
# Transform feature matrix
normalizer.transform(features)array([[ 0.70710678, 0.70710678],
[ 0.30782029, 0.95144452],
[ 0.07405353, 0.99725427],
[ 0.04733062, 0.99887928],
[ 0.95709822, 0.28976368]])Обсуждение
Многие методы изменения масштаба (например, min-max масштабирование и стандартизация) работают с признаками; однако мы также можем изменить масштаб по отдельным наблюдениям. Normalizer изменяет масштаб значений по отдельным наблюдениям, чтобы они имели единичную норму (сумма их длин равна 1). Этот тип изменения масштаба часто используется, когда у нас много эквивалентных признаков (например, классификация текста, когда каждое слово или группа n-слов является признаком).
Normalizer предоставляет три варианта нормы, причем Евклидова норма (часто называемая L2) является аргументом по умолчанию:
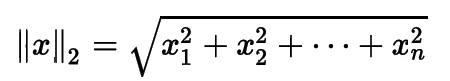
Рисунок: Формула L2-нормы
где x — отдельное наблюдение, а xn — значение этого наблюдения для n-го признака.
# Transform feature matrix
features_l2_norm = Normalizer(norm="l2").transform(features)
# Show feature matrix
features_l2_normarray([[ 0.70710678, 0.70710678],
[ 0.30782029, 0.95144452],
[ 0.07405353, 0.99725427],
[ 0.04733062, 0.99887928],
[ 0.95709822, 0.28976368]])Альтернативно, мы можем указать Манхэттенскую норму (L1):
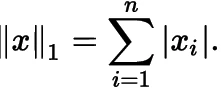
Рисунок: Формула L1-нормы
# Transform feature matrix
features_l1_norm = Normalizer(norm="l1").transform(features)
# Show feature matrix
features_l1_normarray([[ 0.5 , 0.5 ],
[ 0.24444444, 0.75555556],
[ 0.06912442, 0.93087558],
[ 0.04524008, 0.95475992],
[ 0.76760563, 0.23239437]])Интуитивно, норму L2 можно представить как расстояние между двумя точками в Нью-Йорке для птицы (т.е. прямая линия), тогда как норму L1 можно представить как расстояние для человека, идущего по улице (пройти один квартал на север, один квартал на восток, один квартал на север, один квартал на восток и т.д.), поэтому ее называют «Манхэттенской нормой» или «нормой такси».
На практике обратите внимание, что norm='l1' изменяет масштаб значений наблюдения так, чтобы их сумма была равна 1, что иногда может быть желательным свойством:
# Print sum
print("Sum of the first observation\'s values:",
features_l1_norm[0, 0] + features_l1_norm[0, 1])Sum of the first observation's values: 1.04.4 Генерация полиномиальных и интеракционных признаков
Проблема
Вы хотите создать полиномиальные и интеракционные признаки.
Решение
Несмотря на то, что некоторые предпочитают создавать полиномиальные и интеракционные признаки вручную, scikit-learn предлагает встроенный метод:
# Load libraries
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
# Create feature matrix
features = np.array([[2, 3],
[2, 3],
[2, 3]])
# Create PolynomialFeatures object
polynomial_interaction = PolynomialFeatures(degree=2, include_bias=False)
# Create polynomial features
polynomial_interaction.fit_transform(features)array([[ 2., 3., 4., 6., 9.],
[ 2., 3., 4., 6., 9.],
[ 2., 3., 4., 6., 9.]])Параметр degree определяет максимальную степень полинома. Например, degree=2 создаст новые признаки, возведенные во вторую степень:
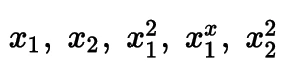
Рисунок: Полиномиальные признаки степени 2
в то время как degree=3 создаст новые признаки, возведенные во вторую и третью степени:
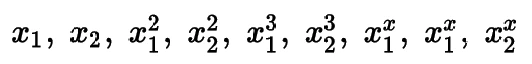
Рисунок: Полиномиальные признаки степени 3
Кроме того, по умолчанию PolynomialFeatures включает интеракционные признаки:
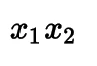
Рисунок: Интеракционный признак
Мы можем ограничить создаваемые признаки только интеракционными признаками, установив interaction_only в True:
interaction = PolynomialFeatures(degree=2,
interaction_only=True, include_bias=False)
interaction.fit_transform(features)array([[ 2., 3., 6.],
[ 2., 3., 6.],
[ 2., 3., 6.]])Обсуждение
Полиномиальные признаки часто создаются, когда мы хотим учесть, что существует нелинейная зависимость между признаками и целевой переменной. Например, мы можем предположить, что влияние возраста на вероятность наличия серьезного заболевания не постоянно со временем, а увеличивается по мере увеличения возраста. Мы можем закодировать это непостоянное влияние в признаке x, сгенерировав более высокие степени этого признака (x2, x3 и т. д.).
Кроме того, часто возникают ситуации, когда влияние одного признака зависит от другого. Простой пример — если бы мы пытались предсказать, сладкий ли наш кофе, и у нас было два признака: 1) был ли кофе перемешан и 2) был ли добавлен сахар. Отдельно каждый признак не предсказывает сладость кофе, но комбинация их влияний — предсказывает. То есть, кофе будет сладким только если в него добавили сахар и перемешали. Влияние каждого признака на целевую переменную (сладость) зависит друг от друга. Мы можем закодировать эту зависимость, включив интеракционный признак, который является произведением отдельных признаков.
4.5 Преобразование признаков
Проблема
Вы хотите выполнить пользовательское преобразование одного или нескольких признаков.
Решение
В scikit-learn используйте FunctionTransformer для применения функции к набору признаков:
# Load libraries
import numpy as np
from sklearn.preprocessing import FunctionTransformer
# Create feature matrix
features = np.array([[2, 3],
[2, 3],
[2, 3]])
# Define a simple function
def add_ten(x: int) -> int:
return x + 10
# Create transformer
ten_transformer = FunctionTransformer(add_ten)
# Transform feature matrix
ten_transformer.transform(features)array([[12, 13],
[12, 13],
[12, 13]])Мы можем создать то же преобразование в pandas, используя apply:
# Load library
import pandas as pd
# Create DataFrame
df = pd.DataFrame(features, columns=["feature_1", "feature_2"])
# Apply function
df.apply(add_ten)| feature_1 | feature_2 | |
|---|---|---|
| 0 | 12 | 13 |
| 1 | 12 | 13 |
| 2 | 12 | 13 |
Обсуждение
Часто хочется выполнить некоторые пользовательские преобразования одного или нескольких признаков. Например, мы можем захотеть создать признак, который является натуральным логарифмом значений другого признака. Мы можем сделать это, создав функцию, а затем применив ее к признакам, используя FunctionTransformer scikit-learn или apply pandas. В решении мы создали очень простую функцию add_ten, которая добавила 10 к каждому входу, но нет причин, по которым мы не могли бы определить гораздо более сложную функцию.
4.6 Обнаружение выбросов
Проблема
Вы хотите выявить экстремальные наблюдения.
Решение
Обнаружение выбросов, к сожалению, больше искусство, чем наука. Однако распространенный метод заключается в предположении, что данные распределены нормально, и на основе этого предположения «нарисовать» эллипс вокруг данных, классифицируя любое наблюдение внутри эллипса как внутреннее (помеченное как 1), а любое наблюдение за пределами эллипса — как выброс (помеченное как -1):
# Load libraries
import numpy as np
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs
# Create simulated data
features, _ = make_blobs(n_samples = 10,
n_features = 2,
centers = 1,
random_state = 1)
# Replace the first observation's values with extreme values
features[0,0] = 10000
features[0,1] = 10000
# Create detector
outlier_detector = EllipticEnvelope(contamination=.1)
# Fit detector
outlier_detector.fit(features)
# Predict outliers
outlier_detector.predict(features)array([-1, 1, 1, 1, 1, 1, 1, 1, 1, 1])В приведенных выше массивах значения -1 относятся к выбросам, тогда как значения 1 относятся к внутренним точкам. Основным ограничением этого подхода является необходимость указать параметр contamination, который представляет собой долю наблюдений, являющихся выбросами — значение, которое мы не знаем. Think of contamination as our estimate of the cleanliness of our data. If we expect our data to have few outliers, we can set contamination to something small. However, if we believe that the data is very likely to have outliers, we can set it to a higher value.
Instead of looking at observations as a whole, we can instead look at individual features and identify extreme values in those features using interquartile range (IQR):
# Create one feature
feature = features[:,0]
# Create a function to return index of outliers
def indicies_of_outliers(x: int) -> np.array(int):
q1, q3 = np.percentile(x, [25, 75])
iqr = q3 - q1
lower_bound = q1 - (iqr * 1.5)
upper_bound = q3 + (iqr * 1.5)
return np.where((x > upper_bound) | (x < lower_bound))
# Run function
indicies_of_outliers(feature)(array([0]),)IQR — это разница между первым и третьим квартилями набора данных. Вы можете представить IQR как разброс основной части данных, причем выбросы — это наблюдения, находящиеся далеко от основного сосредоточения данных. Выбросы обычно определяются как любое значение, которое на 1.5 IQR меньше первого квартиля или на 1.5 IQR больше третьего квартиля.
Обсуждение
Не существует единственной лучшей техники для обнаружения выбросов. Вместо этого у нас есть набор техник, каждая из которых имеет свои преимущества и недостатки. Наша лучшая стратегия часто заключается в попытке использовать несколько техник (например, как EllipticEnvelope, так и обнаружение на основе IQR) и рассмотрении результатов в целом.
По возможности мы должны взглянуть на наблюдения, которые мы выявили как выбросы, и попытаться их понять. Например, если у нас есть набор данных о домах и один признак — количество комнат, является ли выбросом дом со 100 комнатами, или это на самом деле отель, который был неправильно классифицирован?
См. также
Three ways to detect outliers (and the source of the IQR function used in this recipe)
4.7 Обработка выбросов
Проблема
У вас в данных есть выбросы, которые вы хотите выявить, а затем уменьшить их влияние на распределение данных.
Решение
Обычно у нас есть три стратегии для обработки выбросов. Во-первых, мы можем их удалить:
# Load library
import pandas as pd
# Create DataFrame
houses = pd.DataFrame()
houses['Price'] = [534433, 392333, 293222, 4322032]
houses['Bathrooms'] = [2, 3.5, 2, 116]
houses['Square_Feet'] = [1500, 2500, 1500, 48000]
# Filter observations
houses[houses['Bathrooms'] < 20]| Price | Bathrooms | Square_Feet | |
|---|---|---|---|
| 0 | 534433 | 2.0 | 1500 |
| 1 | 392333 | 3.5 | 2500 |
| 2 | 293222 | 2.0 | 1500 |
Во-вторых, мы можем пометить их как выбросы и включить это в качестве признака:
# Load library
import numpy as np
# Create feature based on boolean condition
houses["Outlier"] = np.where(houses["Bathrooms"] < 20, 0, 1)
# Show data
houses| Price | Bathrooms | Square_Feet | Outlier | |
|---|---|---|---|---|
| 0 | 534433 | 2.0 | 1500 | 0 |
| 1 | 392333 | 3.5 | 2500 | 0 |
| 2 | 293222 | 2.0 | 1500 | 0 |
| 3 | 4322032 | 116.0 | 48000 | 1 |
Наконец, мы можем преобразовать признак, чтобы ослабить эффект выброса:
# Log feature
houses["Log_Of_Square_Feet"] = [np.log(x) for x in houses["Square_Feet"]]
# Show data
houses| Price | Bathrooms | Square_Feet | Outlier | Log_Of_Square_Feet | |
|---|---|---|---|---|---|
| 0 | 534433 | 2.0 | 1500 | 0 | 7.313220 |
| 1 | 392333 | 3.5 | 2500 | 0 | 7.824046 |
| 2 | 293222 | 2.0 | 1500 | 0 | 7.313220 |
| 3 | 4322032 | 116.0 | 48000 | 1 | 10.778956 |
Обсуждение
Подобно обнаружению выбросов, не существует жесткого и быстрого правила для их обработки. То, как мы обрабатываем их, должно основываться на двух аспектах. Во-первых, мы должны рассмотреть, что делает их выбросом. Если мы считаем, что это ошибки в данных, например, из-за сломанного датчика или неправильно закодированного значения, тогда мы можем удалить наблюдение или заменить значения выбросов на NaN, поскольку мы не можем доверять этим значениям. Однако, если мы считаем, что выбросы являются подлинными экстремальными значениями (например, дом [особняк] с 200 ванными комнатами), тогда более уместно пометить их как выбросы или преобразовать их значения.
Во-вторых, то, как мы обрабатываем выбросы, должно основываться на нашей цели машинного обучения. Например, если мы хотим предсказать цены на дома на основе признаков дома, мы можем разумно предположить, что цена особняков с более чем 100 ванными комнатами определяется другой динамикой, чем обычных семейных домов. Кроме того, если мы обучаем модель для использования в рамках онлайн-приложения для ипотечного кредитования, мы можем предположить, что наши потенциальные пользователи не будут включать миллиардеров, желающих купить особняк.
Итак, что делать, если у нас есть выбросы? Подумайте, почему они являются выбросами, имейте в виду конечную цель для данных и, самое главное, помните, что непринятие решения по обработке выбросов само по себе является решением с последствиями.
Один дополнительный момент: если у вас есть выбросы, стандартизация может быть неуместной, потому что среднее и дисперсия могут сильно зависеть от выбросов. В этом случае используйте метод масштабирования, более устойчивый к выбросам, такой как RobustScaler.
См. также
RobustScaler documentation
4.8 Дискретизация признаков
Проблема
У вас есть числовой признак, и вы хотите разбить его на дискретные интервалы.
Решение
В зависимости от того, как мы хотим разбить данные, есть две техники, которые мы можем использовать. Во-первых, мы можем бинаризовать признак в соответствии с некоторым порогом:
# Load libraries
import numpy as np
from sklearn.preprocessing import Binarizer
# Create feature
age = np.array([[6],
[12],
[20],
[36],
[65]])
# Create binarizer
binarizer = Binarizer(threshold=18)
# Transform feature
binarizer.fit_transform(age)array([[0],
[0],
[1],
[1],
[1]])Во-вторых, мы можем разбить числовые признаки в соответствии с несколькими порогами:
# Bin feature
np.digitize(age, bins=[20,30,64])array([[0],
[0],
[1],
[2],
[3]])Обратите внимание, что аргументы для параметра bins обозначают левый край каждого интервала. Например, аргумент 20 не включает элемент со значением 20, только два значения меньше 20. Мы можем изменить это поведение, установив параметр right в True:
# Bin feature
np.digitize(age, bins=[20,30,64], right=True)array([[0],
[0],
[0],
[2],
[3]])Обсуждение
Дискретизация может быть плодотворной стратегией, когда у нас есть основания полагать, что числовой признак должен вести себя скорее как категориальный признак. Например, мы можем полагать, что существует очень небольшая разница в привычках расходов у 19- и 20-летних, но значительная разница между 20- и 21-летними (возраст в Соединенных Штатах, когда молодые люди могут употреблять алкоголь). В этом примере может быть полезно разбить людей в наших данных на тех, кто может употреблять алкоголь, и тех, кто не может. Аналогично, в других случаях может быть полезно дискретизировать наши данные на три или более интервала.
В решении мы рассмотрели два метода дискретизации — Binarizer scikit-learn для двух интервалов и digitize NumPy для трех или более интервалов — однако мы также можем использовать digitize для бинаризации признаков, подобно Binarizer, просто указав один порог:
# Bin feature
np.digitize(age, bins=[18])array([[0],
[0],
[1],
[1],
[1]])См. также
digitize documentation
4.9 Группировка наблюдений с использованием кластеризации
Проблема
Вы хотите кластеризовать наблюдения так, чтобы похожие наблюдения были сгруппированы вместе.
Решение
Если вы знаете, что у вас есть k групп, вы можете использовать k-means кластеризацию для группировки похожих наблюдений и вывода нового признака, содержащего принадлежность каждого наблюдения к группе:
# Load libraries
import pandas as pd
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# Make simulated feature matrix
features, _ = make_blobs(n_samples = 50,
n_features = 2,
centers = 3,
random_state = 1)
# Create DataFrame
dataframe = pd.DataFrame(features, columns=["feature_1", "feature_2"])
# Make k-means clusterer
clusterer = KMeans(3, random_state=0)
# Fit clusterer
clusterer.fit(features)
# Predict values
dataframe["group"] = clusterer.predict(features)
# View first few observations
dataframe.head(5)| feature_1 | feature_2 | group | |
|---|---|---|---|
| 0 | –9.877554 | –3.336145 | 0 |
| 1 | –7.287210 | –8.353986 | 2 |
| 2 | –6.943061 | –7.023744 | 2 |
| 3 | –7.440167 | –8.791959 | 2 |
| 4 | –6.641388 | –8.075888 | 2 |
Обсуждение
Мы немного забегаем вперед и более подробно остановимся на алгоритмах кластеризации далее в книге. Однако я хотел отметить, что мы можем использовать кластеризацию в качестве шага предварительной обработки.
В частности, мы используем алгоритмы обучения без учителя, такие как k-means, для кластеризации наблюдений в группы. Конечным результатом является категориальный признак, где похожие наблюдения являются членами одной и той же группы.
Не волнуйтесь, если вы не поняли всего этого прямо сейчас: просто запомните идею, что кластеризация может быть использована в предварительной обработке. И если вы действительно не можете ждать, смело переходите к [Ссылка на главу] сейчас.
4.10 Удаление наблюдений с пропущенными значениями
Проблема
Вам нужно удалить наблюдения, содержащие пропущенные значения.
Решение
Удалить наблюдения с пропущенными значениями легко с помощью хитрой строки NumPy:
# Load library
import numpy as np
# Create feature matrix
features = np.array([[1.1, 11.1],
[2.2, 22.2],
[3.3, 33.3],
[4.4, 44.4],
[np.nan, 55]])
# Keep only observations that are not (denoted by ~) missing
features[~np.isnan(features).any(axis=1)]array([[ 1.1, 11.1],
[ 2.2, 22.2],
[ 3.3, 33.3],
[ 4.4, 44.4]])Альтернативно, мы можем удалить пропущенные наблюдения с помощью pandas:
# Load library
import pandas as pd
# Load data
dataframe = pd.DataFrame(features, columns=["feature_1", "feature_2"])
# Remove observations with missing values
dataframe.dropna()| feature_1 | feature_2 | |
|---|---|---|
| 0 | 1.1 | 11.1 |
| 1 | 2.2 | 22.2 |
| 2 | 3.3 | 33.3 |
| 3 | 4.4 | 44.4 |
Обсуждение
Большинство алгоритмов машинного обучения не могут обрабатывать пропущенные значения в целевом и признаковом массивах. По этой причине мы не можем игнорировать пропущенные значения в наших данных и должны решить эту проблему во время предварительной обработки.
Самое простое решение — удалить каждое наблюдение, содержащее одно или несколько пропущенных значений, задача, быстро и легко решаемая с помощью NumPy или pandas.
Сказав это, мы должны очень неохотно удалять наблюдения с пропущенными значениями. Удаление их — это крайняя мера, поскольку наш алгоритм теряет доступ к информации, содержащейся в непропущенных значениях наблюдения.
Не менее важно, что в зависимости от причины пропущенных значений, удаление наблюдений может внести смещение в наши данные. Существует три типа пропущенных данных:
Missing Completely At Random (MCAR)
Вероятность того, что значение отсутствует, не зависит ни от чего. Например, респондент опроса бросает кубик перед ответом на вопрос: если выпадет шестерка, она пропускает этот вопрос.
Missing At Random (MAR)
Вероятность того, что значение отсутствует, не является полностью случайной, но зависит от информации, содержащейся в других признаках. Например, опрос спрашивает о гендерной идентичности и годовой зарплате, и женщины чаще пропускают вопрос о зарплате; однако их отказ от ответа зависит только от информации, которую мы собрали в признаке гендерной идентичности.
Missing Not At Random (MNAR)
Вероятность того, что значение отсутствует, не является случайной и зависит от информации, не содержащейся в наших признаках. Например, опрос спрашивает о гендерной идентичности, и женщины чаще пропускают вопрос о зарплате, а у нас нет признака гендерной идентичности в наших данных.
Иногда допустимо удалять наблюдения, если они MCAR или MAR. Однако, если значение MNAR, сам факт отсутствия значения является информацией. Удаление наблюдений MNAR может внести смещение в наши данные, потому что мы удаляем наблюдения, вызванные некоторым ненаблюдаемым систематическим эффектом.
См. также
Identifying the Three Types of Missing Data
Missing-Data Imputation
4.11 Импутация пропущенных значений
Проблема
У вас в данных есть пропущенные значения, и вы хотите заменить их с помощью некоторого общего метода или предсказания.
Решение
Вы можете импутировать пропущенные значения с помощью k-ближайших соседей (KNN) или класса SimpleImputer scikit-learn. Если у вас небольшой объем данных, предскажите и импутируйте пропущенные значения с помощью k-ближайших соседей (KNN):
# Load libraries
import numpy as np
from sklearn.impute import KNNImputer
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs
# Make a simulated feature matrix
features, _ = make_blobs(n_samples = 1000,
n_features = 2,
random_state = 1)
# Standardize the features
scaler = StandardScaler()
standardized_features = scaler.fit_transform(features)
# Replace the first feature's first value with a missing value
true_value = standardized_features[0,0]
standardized_features[0,0] = np.nan
# Predict the missing values in the feature matrix
knn_imputer = KNNImputer(n_neighbors=5)
features_knn_imputed = knn_imputer.fit_transform(standardized_features)
# Compare true and imputed values
print("True Value:", true_value)
print("Imputed Value:", features_knn_imputed[0,0])True Value: 0.8730186114
Imputed Value: 1.09553327131Альтернативно, мы можем использовать класс SimpleImputer scikit-learn из модуля imputer для заполнения пропущенных значений средним, медианой или наиболее частым значением признака. Однако мы, как правило, получим худшие результаты, чем с KNN:
# Load library
import numpy as np
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs
# Make a simulated feature matrix
features, _ = make_blobs(n_samples = 1000,
n_features = 2,
random_state = 1)
# Standardize the features
scaler = StandardScaler()
standardized_features = scaler.fit_transform(features)
# Replace the first feature's first value with a missing value
true_value = standardized_features[0,0]
standardized_features[0,0] = np.nan
# Create imputer using the "mean" strategy
mean_imputer = SimpleImputer(strategy="mean")
# Impute values
features_mean_imputed = mean_imputer.fit_transform(features)
# Compare true and imputed values
print("True Value:", true_value)
print("Imputed Value:", features_mean_imputed[0,0])True Value: 0.8730186114
Imputed Value: -3.05837272461Обсуждение
Когда у нас есть пропущенные значения в категориальном признаке, наше лучшее решение — открыть наш набор инструментов алгоритмов машинного обучения для предсказания значений пропущенных наблюдений. Мы можем добиться этого, рассматривая признак с пропущенными значениями как целевой вектор, а остальные подмножества признаков — как матрицу признаков. Часто используемый алгоритм — KNN (подробно рассмотренный далее в этой книге), который присваивает пропущенному значению наиболее частый класс из k ближайших наблюдений.
Альтернативно, мы можем заполнить пропущенные значения наиболее частым классом признака. Хотя это менее изощренный метод, чем KNN, он гораздо более масштабируем для больших данных. В любом случае, рекомендуется включить бинарный признак, указывающий, содержат ли наблюдения импутированные значения.
См. также
Imputation of missing values with scikit-learn
A Study of K-Nearest Neighbour as an Imputation Method
5.5 Обработка несбалансированных классов
Проблема
У вас есть целевой вектор с сильно несбалансированными классами, и вы хотите внести коррективы, чтобы справиться с несбалансированностью классов.
Решение
Соберите больше данных. Если это невозможно, измените метрики, используемые для оценки вашей модели. Если это не работает, рассмотрите возможность использования встроенных параметров веса класса модели (если доступны), даунсэмплинга или апсэмплинга. Мы рассмотрим метрики оценки в более поздней главе, поэтому пока сосредоточимся на параметрах веса класса, даунсэмплинге и апсэмплинге.
Чтобы продемонстрировать наши решения, нам нужно создать некоторые данные с несбалансированными классами. Набор данных Ириса Фишера содержит три сбалансированных класса по 50 наблюдений каждый, указывающих вид цветка (Iris setosa, Iris virginica и Iris versicolor). Чтобы сделать набор данных несбалансированным, мы удаляем 40 из 50 наблюдений Iris setosa, а затем объединяем классы Iris virginica и Iris versicolor. Конечным результатом является бинарный целевой вектор, указывающий, является ли наблюдение цветком Iris setosa или нет. Результат — 10 наблюдений Iris setosa (класс 0) и 100 наблюдений не Iris setosa (класс 1):
# Load libraries
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
# Load iris data
iris = load_iris()
# Create feature matrix
features = iris.data
# Create target vector
target = iris.target
# Remove first 40 observations
features = features[40:,:]
target = target[40:]
# Create binary target vector indicating if class 0
target = np.where((target == 0), 0, 1)
# Look at the imbalanced target vector
targetarray([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1])Многие алгоритмы в scikit-learn предлагают параметр для взвешивания классов во время обучения, чтобы противодействовать эффекту их несбалансированности. Хотя мы еще не рассмотрели его, RandomForestClassifier — популярный алгоритм классификации, который включает параметр class_weight. Вы можете передать аргумент, явно указывающий желаемые веса классов:
# Create weights
weights = {0: .9, 1: 0.1}
# Create random forest classifier with weights
RandomForestClassifier(class_weight=weights)RandomForestClassifier(class_weight={0: 0.9, 1: 0.1})Или вы можете передать balanced, который автоматически создает веса, обратно пропорциональные частотам классов:
# Train a random forest with balanced class weights
RandomForestClassifier(class_weight="balanced")RandomForestClassifier(class_weight='balanced')Альтернативно, мы можем снизить выборку (downsample) мажоритарного класса или увеличить выборку (upsample) миноритарного класса. При снижении выборки мы случайно выбираем без замены из мажоритарного класса (т.е. класса с большим количеством наблюдений), чтобы создать новое подмножество наблюдений, равное по размеру миноритарному классу. Например, если миноритарный класс имеет 10 наблюдений, мы случайно выберем 10 наблюдений из мажоритарного класса и используем эти 20 наблюдений в качестве наших данных. Здесь мы делаем именно это, используя наши несбалансированные данные Ириса:
# Indicies of each class' observations
i_class0 = np.where(target == 0)[0]
i_class1 = np.where(target == 1)[0]
# Number of observations in each class
n_class0 = len(i_class0)
n_class1 = len(i_class1)
# For every observation of class 0, randomly sample
# from class 1 without replacement
i_class1_downsampled = np.random.choice(i_class1, size=n_class0, replace=False)
# Join together class 0's target vector with the
# downsampled class 1's target vector
np.hstack((target[i_class0], target[i_class1_downsampled]))array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])# Join together class 0's feature matrix with the
# downsampled class 1's feature matrix
np.vstack((features[i_class0,:], features[i_class1_downsampled,:]))[0:5]array([[ 5. , 3.5, 1.3, 0.3],
[ 4.5, 2.3, 1.3, 0.3],
[ 4.4, 3.2, 1.3, 0.2],
[ 5. , 3.5, 1.6, 0.6],
[ 5.1, 3.8, 1.9, 0.4]])Другой вариант — увеличить выборку миноритарного класса. При увеличении выборки для каждого наблюдения в мажоритарном классе мы случайно выбираем наблюдение из миноритарного класса с заменой. Конечным результатом является одинаковое количество наблюдений из миноритарного и мажоритарного классов. Увеличение выборки реализуется очень похоже на снижение выборки, только наоборот:
# For every observation in class 1, randomly sample from class 0 with replacement
i_class0_upsampled = np.random.choice(i_class0, size=n_class1, replace=True)
# Join together class 0's upsampled target vector with class 1's target vector
np.concatenate((target[i_class0_upsampled], target[i_class1]))array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])# Join together class 0's upsampled feature matrix with class 1's feature matrix
np.vstack((features[i_class0_upsampled,:], features[i_class1,:]))[0:5]array([[ 5. , 3.5, 1.6, 0.6],
[ 5. , 3.5, 1.6, 0.6],
[ 5. , 3.3, 1.4, 0.2],
[ 4.5, 2.3, 1.3, 0.3],
[ 4.8, 3. , 1.4, 0.3]])Обсуждение
В реальном мире несбалансированные классы встречаются повсеместно — большинство посетителей не нажимают кнопку покупки, и многие типы рака, к счастью, редки. По этой причине обработка несбалансированных классов является распространенной задачей в машинном обучении.
Наша лучшая стратегия — просто собрать больше наблюдений — особенно наблюдений миноритарного класса. Однако это часто невозможно, поэтому нам приходится прибегать к другим вариантам.
Вторая стратегия — использовать метрику оценки модели, лучше подходящую для несбалансированных классов. Точность часто используется в качестве метрики для оценки производительности модели, но при наличии несбалансированных классов точность может быть плохо подходящей. Например, если только у 0.5% наблюдений есть редкий рак, то даже наивная модель, которая предсказывает, что ни у кого нет рака, будет иметь точность 99.5%. Ясно, что это не идеальный вариант. Некоторые лучшие метрики, которые мы обсудим в более поздних главах, — это матрицы ошибок, точность (precision), полнота (recall), F1-метрика и ROC-кривые.
Третья стратегия — использовать параметры взвешивания классов, включенные в реализации некоторых моделей. Это позволяет алгоритму корректировать несбалансированные классы. К счастью, многие классификаторы scikit-learn имеют параметр class_weight, что делает его хорошим вариантом.
Четвертая и пятая стратегии связаны: снижение выборки (downsampling) и увеличение выборки (upsampling). При снижении выборки мы создаем случайное подмножество мажоритарного класса, равное по размеру миноритарному классу. При увеличении выборки мы многократно выбираем с заменой из миноритарного класса, чтобы сделать его равным по размеру мажоритарному классу. Решение между использованием снижения выборки и увеличения выборки зависит от контекста, и в целом мы должны попробовать оба варианта, чтобы увидеть, какой дает лучшие результаты.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- 100 Страниц о машинном обучении
- Математика для нейронного обучения