Глава 1. Работа с векторами, матрицами и массивами в NumPy
Примечание
С электронными книгами в раннем доступе вы получаете книги в их самой ранней форме — необработанный и неотредактированный контент авторов по мере их написания — так что вы можете воспользоваться этими технологиями задолго до официального выпуска этих изданий.
Это будет 1-я глава финальной книги.
Если у вас есть комментарии о том, как мы можем улучшить содержание и/или примеры в этой книге, или если вы заметили отсутствующий материал в этой главе, пожалуйста, свяжитесь с авторами по адресу
feedback.mlpythoncookbook@gmail.com.
1.0 Введение
NumPy является основополагающим инструментом стека машинного обучения на Python. NumPy позволяет эффективно работать со структурами данных, часто используемыми в машинном обучении: векторами, матрицами и тензорами. Хотя NumPy не является основным предметом этой книги, он будет часто встречаться в последующих главах. Эта глава охватывает наиболее распространенные операции NumPy, с которыми мы, вероятно, столкнемся при работе с рабочими процессами машинного обучения.
1.1 Создание вектора
Проблема
Вам нужно создать вектор.
Решение
Используйте NumPy для создания одномерного массива:
# Load library
import numpy as np
# Create a vector as a row
vector_row = np.array([1, 2, 3])
# Create a vector as a column
vector_column = np.array([[1],
[2],
[3]])Обсуждение
Основной структурой данных NumPy является многомерный массив. Вектор — это просто массив с одной размерностью. Чтобы создать вектор, мы просто создаем одномерный массив. Как и векторы, эти массивы могут быть представлены горизонтально (т.е. строками) или вертикально (т.е. столбцами).
См. также
Vectors, Math Is Fun
Euclidean vector, Wikipedia
1.2 Создание матрицы
Проблема
Вам нужно создать матрицу.
Решение
Используйте NumPy для создания двумерного массива:
# Load library
import numpy as np
# Create a matrix
matrix = np.array([[1, 2],
[1, 2],
[1, 2]])Обсуждение
Чтобы создать матрицу, мы можем использовать двумерный массив NumPy. В нашем решении матрица содержит три строки и два столбца (столбец из 1 и столбец из 2).
У NumPy на самом деле есть специальная структура данных для матриц:
matrix_object = np.mat([[1, 2],
[1, 2],
[1, 2]])matrix([[1, 2],
[1, 2],
[1, 2]])Однако структура данных для матриц не рекомендуется по двум причинам. Во-первых, массивы являются фактической стандартной структурой данных NumPy. Во-вторых, подавляющее большинство операций NumPy возвращают массивы, а не объекты матриц.
См. также
Matrix, Wikipedia
Matrix, Wolfram MathWorld
1.3 Создание разреженной матрицы
Проблема
Учитывая данные с очень небольшим количеством ненулевых значений, вы хотите эффективно их представить.
Решение
Создайте разреженную матрицу:
# Load libraries
import numpy as np
from scipy import sparse
# Create a matrix
matrix = np.array([[0, 0],
[0, 1],
[3, 0]])
# Create compressed sparse row (CSR) matrix
matrix_sparse = sparse.csr_matrix(matrix)Обсуждение
Частая ситуация в машинном обучении — наличие огромного объема данных; однако большинство элементов в данных равны нулю. Например, представьте себе матрицу, где столбцами являются все фильмы на Netflix, строками — все пользователи Netflix, а значениями — сколько раз пользователь посмотрел тот или иной фильм. Эта матрица будет иметь десятки тысяч столбцов и миллионы строк! Однако, поскольку большинство пользователей не смотрят большинство фильмов, подавляющее большинство элементов будут равны нулю.
Разреженная матрица — это матрица, в которой большинство элементов равны 0. Разреженные матрицы хранят только ненулевые элементы и предполагают, что все остальные значения будут равны нулю, что приводит к значительной экономии вычислительных ресурсов. В нашем решении мы создали массив NumPy с двумя ненулевыми значениями, а затем преобразовали его в разреженную матрицу. Если мы посмотрим на разреженную матрицу, мы увидим, что хранятся только ненулевые значения:
# View sparse matrix
print(matrix_sparse)(1, 1) 1
(2, 0) 3
Существует несколько типов разреженных матриц. Однако в compressed sparse row
(CSR) матрицах (1, 1) и (2, 0) представляют (нулевые) индексы ненулевых значений 1 и 3 соответственно. Например, элемент 1 находится во второй строке и втором столбце. Мы можем увидеть преимущество разреженных матриц, если создадим гораздо большую матрицу с гораздо большим количеством нулевых элементов, а затем сравним эту большую матрицу с нашей исходной разреженной матрицей:
# Create larger matrix
matrix_large = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[3, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
# Create compressed sparse row (CSR) matrix
matrix_large_sparse = sparse.csr_matrix(matrix_large)
# View original sparse matrix
print(matrix_sparse)(1, 1) 1
(2, 0) 3# View larger sparse matrix
print(matrix_large_sparse)(1, 1) 1
(2, 0) 3Как мы видим, несмотря на то, что мы добавили гораздо больше нулевых элементов в большую матрицу, ее разреженное представление точно такое же, как и у нашей исходной разреженной матрицы. То есть добавление нулевых элементов не изменило размер разреженной матрицы.
Как уже упоминалось, существует множество различных типов разреженных матриц, таких как compressed sparse column, list of lists и dictionary of keys. Хотя объяснение различных типов и их последствий выходит за рамки этой книги, стоит отметить, что, хотя нет “лучшего” типа разреженной матрицы, между ними есть значимые различия, и мы должны осознавать, почему мы выбираем один тип над другим.
См. также
Sparse matrices, SciPy documentation
101 Ways to Store a Sparse Matrix
1.4 Предварительное выделение массивов Numpy
Проблема
Вам нужно предварительно выделить массивы заданного размера с некоторым значением.
Решение
NumPy имеет функции для генерации векторов и матриц любого размера, используя 0, 1 или значения по вашему выбору.
# Load library
import numpy as np
# Generate a vector of shape (1,5) containing all zeros
vector = np.zeros(shape=5)
# View the vector
print(vector)array([0., 0., 0., 0., 0.])# Generate a matrix of shape (3,3) containing all ones
matrix = np.full(shape=(3,3), fill_value=1)
# View the vector
print(matrix)array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])Обсуждение
Генерация массивов, предварительно заполненных данными, полезна для ряда целей, таких как повышение производительности кода или наличие синтетических данных для тестирования алгоритмов. Во многих языках программирования предварительное выделение массива значений по умолчанию (например, 0) считается общепринятой практикой.
1.5 Выбор элементов
Проблема
Вам нужно выбрать один или несколько элементов в векторе или матрице.
Решение
Массивы NumPy позволяют легко выбирать элементы в векторах или матрицах:
# Load library
import numpy as np
# Create row vector
vector = np.array([1, 2, 3, 4, 5, 6])
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Select third element of vector
vector[2]3# Select second row, second column
matrix[1,1]5Обсуждение
Как и большинство вещей в Python, массивы NumPy имеют нулевую индексацию, что означает, что индекс первого элемента равен 0, а не 1. С этим предостережением NumPy предлагает широкий спектр методов для выбора (т.е. индексирования и нарезки) элементов или групп элементов в массивах:
# Select all elements of a vector
vector[:]array([1, 2, 3, 4, 5, 6])# Select everything up to and including the third element
vector[:3]array([1, 2, 3])# Select everything after the third element
vector[3:]array([4, 5, 6])# Select the last element
vector[-1]6# Reverse the vector
vector[::-1]array([6, 5, 4, 3, 2, 1])# Select the first two rows and all columns of a matrix
matrix[:2,:]array([[1, 2, 3],
[4, 5, 6]])# Select all rows and the second column
matrix[:,1:2]array([[2],
[5],
[8]])1.6 Описание матрицы
Проблема
Вы хотите описать форму, размер и размерность матрицы.
Решение
Используйте атрибуты shape, size и ndim объекта NumPy:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
# View number of rows and columns
matrix.shape(3, 4)# View number of elements (rows * columns)
matrix.size12# View number of dimensions
matrix.ndim2Обсуждение
Это может показаться простым (и это так); однако снова и снова будет полезно проверить форму и размер массива как для дальнейших расчетов, так и просто в качестве быстрой проверки после какой-либо операции.
1.7 Применение функций ко всем элементам
Проблема
Вам нужно применить некоторую функцию ко всем элементам массива.
Решение
Используйте метод vectorize NumPy:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Create function that adds 100 to something
add_100 = lambda i: i + 100
# Create vectorized function
vectorized_add_100 = np.vectorize(add_100)
# Apply function to all elements in matrix
vectorized_add_100(matrix)array([[101, 102, 103],
[104, 105, 106],
[107, 108, 109]])Обсуждение
Класс vectorize NumPy преобразует функцию в функцию, которую можно применить ко всем элементам массива или его срезу. Стоит отметить, что vectorize по сути является циклом for по элементам и не повышает производительность. Кроме того, массивы NumPy позволяют выполнять операции между массивами, даже если их размерности не совпадают (процесс, называемый broadcasting). Например, мы можем создать гораздо более простую версию нашего решения, используя broadcasting:
# Add 100 to all elements
matrix + 100array([[101, 102, 103],
[104, 105, 106],
[107, 108, 109]])Broadcasting работает не для всех форм и ситуаций, но это распространенный способ применения простых операций ко всем элементам массива numpy.
1.8 Нахождение максимального и минимального значений
Проблема
Вам нужно найти максимальное или минимальное значение в массиве.
Решение
Используйте методы max и min NumPy:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Return maximum element
np.max(matrix)9# Return minimum element
np.min(matrix)1Обсуждение
Часто мы хотим узнать максимальное и минимальное значение в массиве или его подмножестве. Это можно сделать с помощью методов max и min. Используя параметр axis, мы также можем применить операцию вдоль определенной оси:
# Find maximum element in each column
np.max(matrix, axis=0)array([7, 8, 9])# Find maximum element in each row
np.max(matrix, axis=1)array([3, 6, 9])1.9 Вычисление среднего, дисперсии и стандартного отклонения
Проблема
Вы хотите вычислить некоторые описательные статистики о массиве.
Решение
Используйте mean, var и std NumPy:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Return mean
np.mean(matrix)5.0# Return variance
np.var(matrix)6.666666666666667# Return standard deviation
np.std(matrix)2.5819888974716112Обсуждение
Как и с max и min, мы можем легко получить описательные статистики обо всей матрице или выполнить расчеты вдоль одной оси:
# Find the mean value in each column
np.mean(matrix, axis=0)array([ 4., 5., 6.])1.10 Изменение формы массивов
Проблема
Вы хотите изменить форму (количество строк и столбцов) массива, не изменяя значения элементов.
Решение
Используйте reshape NumPy:
# Load library
import numpy as np
# Create 4x3 matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
# Reshape matrix into 2x6 matrix
matrix.reshape(2, 6)array([[ 1, 2, 3, 4, 5, 6],
[ 7, 8, 9, 10, 11, 12]])Обсуждение
reshape позволяет нам реструктурировать массив таким образом, чтобы сохранить те же данные, но они были организованы в другом количестве строк и столбцов. Единственное требование заключается в том, чтобы форма исходной и новой матрицы содержала одинаковое количество элементов (т.е. одинаковый размер). Мы можем увидеть размер матрицы, используя size:
matrix.size12Один полезный аргумент в reshape — это -1, что фактически означает “сколько нужно”, поэтому reshape(1, -1) означает одну строку и столько столбцов, сколько нужно:
matrix.reshape(1, -1)array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]])Наконец, если мы предоставим одно целое число, reshape вернет одномерный массив такой длины:
matrix.reshape(12)array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])1.11 Транспонирование вектора или матрицы
Проблема
Вам нужно транспонировать вектор или матрицу.
Решение
Используйте метод T:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Transpose matrix
matrix.Tarray([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])Обсуждение
Транспонирование — распространенная операция в линейной алгебре, при которой индексы столбцов и строк каждого элемента меняются местами. Один нюанс, который обычно упускается за пределами класса линейной алгебры, заключается в том, что технически вектор не может быть транспонирован, потому что это просто набор значений:
# Transpose vector
np.array([1, 2, 3, 4, 5, 6]).Tarray([1, 2, 3, 4, 5, 6])Однако обычно транспонирование вектора называют преобразованием вектора-строки в вектор-столбец (обратите внимание на вторую пару скобок) или наоборот:
# Tranpose row vector
np.array([[1, 2, 3, 4, 5, 6]]).Tarray([[1],
[2],
[3],
[4],
[5],
[6]])1.12 Сглаживание матрицы
Проблема
Вам нужно преобразовать матрицу в одномерный массив.
Решение
Используйте flatten:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Flatten matrix
matrix.flatten()array([1, 2, 3, 4, 5, 6, 7, 8, 9])Обсуждение
flatten — это простой метод преобразования матрицы в одномерный массив. Альтернативно, мы можем использовать reshape для создания вектора-строки:
matrix.reshape(1, -1)array([[1, 2, 3, 4, 5, 6, 7, 8, 9]])Еще один распространенный метод сглаживания массивов — это метод ravel. В отличие от flatten, который возвращает копию исходного массива, ravel работает с самим исходным объектом и поэтому немного быстрее. Он также позволяет сглаживать списки массивов, чего мы не можем сделать с методом flatten. Эта операция полезна для сглаживания очень больших массивов и ускорения кода.
# Create one matrix
matrix_a = np.array([[1, 2],
[3, 4]])
# Create a second matrix
matrix_b = np.array([[5, 6],
[7, 8]])
# Create a list of matrices
matrix_list = [matrix_a, matrix_b]
# Flatten the entire list of matrices
np.ravel(matrix_list)array([1, 2, 3, 4, 5, 6, 7, 8])1.13 Нахождение ранга матрицы
Проблема
Вам нужно узнать ранг матрицы.
Решение
Используйте метод линейной алгебры NumPy matrix_rank:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 1, 1],
[1, 1, 10],
[1, 1, 15]])
# Return matrix rank
np.linalg.matrix_rank(matrix)2Обсуждение
Ранг матрицы — это размерность векторного пространства, натянутого на ее столбцы или строки. Найти ранг матрицы легко в NumPy благодаря matrix_rank.
См. также
The Rank of a Matrix, CliffsNotes
1.14 Получение диагонали матрицы
Проблема
Вам нужно получить диагональные элементы матрицы.
Решение
Используйте diagonal:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[2, 4, 6],
[3, 8, 9]])
# Return diagonal elements
matrix.diagonal()array([1, 4, 9])Обсуждение
NumPy упрощает получение диагональных элементов матрицы с помощью diagonal. Также можно получить диагональ, смещенную от главной диагонали, используя параметр offset:
# Return diagonal one above the main diagonal
matrix.diagonal(offset=1)array([2, 6])# Return diagonal one below the main diagonal
matrix.diagonal(offset=-1)array([2, 8])1.15 Вычисление следа матрицы
Проблема
Вам нужно вычислить след матрицы.
Решение
Используйте trace:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 2, 3],
[2, 4, 6],
[3, 8, 9]])
# Return trace
matrix.trace()14Обсуждение
След матрицы — это сумма диагональных элементов, и он часто используется в методах машинного обучения. Имея многомерный массив NumPy, мы можем вычислить след, используя trace. Мы также можем вернуть диагональ матрицы и вычислить ее сумму:
# Return diagonal and sum elements
sum(matrix.diagonal())14См. также
The Trace of a Square Matrix
1.16 Вычисление скалярных произведений
Проблема
Вам нужно вычислить скалярное произведение двух векторов.
Решение
Используйте dot NumPy:
# Load library
import numpy as np
# Create two vectors
vector_a = np.array([1,2,3])
vector_b = np.array([4,5,6])
# Calculate dot product
np.dot(vector_a, vector_b)32Обсуждение
Скалярное произведение двух векторов, a и b, определяется как:
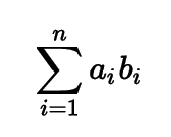
Рисунок: Формула скалярного произведения
где ai — i-й элемент вектора a, а bi — i-й элемент вектора b. Мы можем использовать функцию dot NumPy для вычисления скалярного произведения. Альтернативно, в Python 3.5+ мы можем использовать новый оператор @:
# Calculate dot product
vector_a @ vector_b32См. также
Vector dot product and vector length, Khan Academy
Dot Product, Paul’s Online Math Notes
1.17 Сложение и вычитание матриц
Проблема
Вы хотите сложить или вычесть две матрицы.
Решение
Используйте add и subtract NumPy:
# Load library
import numpy as np
# Create matrix
matrix_a = np.array([[1, 1, 1],
[1, 1, 1],
[1, 1, 2]])
# Create matrix
matrix_b = np.array([[1, 3, 1],
[1, 3, 1],
[1, 3, 8]])
# Add two matrices
np.add(matrix_a, matrix_b)array([[ 2, 4, 2],
[ 2, 4, 2],
[ 2, 4, 10]])# Subtract two matrices
np.subtract(matrix_a, matrix_b)array([[ 0, -2, 0],
[ 0, -2, 0],
[ 0, -2, -6]])Обсуждение
Альтернативно, мы можем просто использовать операторы + и -:
# Add two matrices
matrix_a + matrix_barray([[ 2, 4, 2],
[ 2, 4, 2],
[ 2, 4, 10]])1.18 Умножение матриц
Проблема
Вы хотите умножить две матрицы.
Решение
Используйте dot NumPy:
# Load library
import numpy as np
# Create matrix
matrix_a = np.array([[1, 1],
[1, 2]])
# Create matrix
matrix_b = np.array([[1, 3],
[1, 2]])
# Multiply two matrices
np.dot(matrix_a, matrix_b)array([[2, 5],
[3, 7]])Обсуждение
Альтернативно, в Python 3.5+ мы можем использовать оператор @:
# Multiply two matrices
matrix_a @ matrix_barray([[2, 5],
[3, 7]])Если мы хотим выполнить поэлементное умножение, мы можем использовать оператор *:
# Multiply two matrices element-wise
matrix_a * matrix_barray([[1, 3],
[1, 4]])См. также
Array vs. Matrix Operations, MathWorks
1.19 Инвертирование матрицы
Проблема
Вам нужно вычислить обратную матрицу квадратной матрицы.
Решение
Используйте метод линейной алгебры NumPy inv:
# Load library
import numpy as np
# Create matrix
matrix = np.array([[1, 4],
[2, 5]])
# Calculate inverse of matrix
np.linalg.inv(matrix)array([[-1.66666667, 1.33333333],
[ 0.66666667, -0.33333333]])Обсуждение
Обратная матрица квадратной матрицы A — это вторая матрица A–1, такая что:
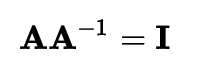
Рисунок: Формула обратной матрицы
где I — единичная матрица. В NumPy мы можем использовать linalg.inv для вычисления A–1, если она существует. Чтобы увидеть это в действии, мы можем умножить матрицу на ее обратную, и результатом будет единичная матрица:
# Multiply matrix and its inverse
matrix @ np.linalg.inv(matrix)array([[ 1., 0.],
[ 0., 1.]])См. также
Inverse of a Matrix
1.20 Генерация случайных значений
Проблема
Вы хотите сгенерировать псевдослучайные значения.
Решение
Используйте random NumPy:
# Load library
import numpy as np
# Set seed
np.random.seed(0)
# Generate three random floats between 0.0 and 1.0
np.random.random(3)array([ 0.5488135 , 0.71518937, 0.60276338])Обсуждение
NumPy предлагает широкий спектр средств для генерации случайных чисел, гораздо больше, чем можно охватить здесь. В нашем решении мы генерировали числа с плавающей точкой; однако также часто генерируют целые числа:
# Generate three random integers between 0 and 10
np.random.randint(0, 11, 3)array([3, 7, 9])Альтернативно, мы можем генерировать числа, выбирая их из распределения (обратите внимание, что это не является технически случайным):
# Draw three numbers from a normal distribution with mean 0.0
# and standard deviation of 1.0
np.random.normal(0.0, 1.0, 3)array([-1.42232584, 1.52006949, -0.29139398])# Draw three numbers from a logistic distribution with mean 0.0 and scale of 1.0
np.random.logistic(0.0, 1.0, 3)array([-0.98118713, -0.08939902, 1.46416405])# Draw three numbers greater than or equal to 1.0 and less than 2.0
np.random.uniform(1.0, 2.0, 3)array([ 1.47997717, 1.3927848 , 1.83607876])Наконец, иногда бывает полезно получить одни и те же случайные числа несколько раз, чтобы получить предсказуемые, повторяемые результаты. Мы можем сделать это, установив “зерно” (целое число) генератора псевдослучайных чисел. Случайные процессы с одним и тем же зерном всегда будут давать один и тот же результат. Мы будем использовать зерна по всей этой книге, чтобы код, который вы видите в книге, и код, который вы запускаете на своем компьютере, давали одинаковые результаты.
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- 100 Страниц о машинном обучении
- Математика для нейронного обучения