Глава 10. Уменьшение размерности с использованием выбора признаков
10.0 Введение
В Главе 9 мы обсуждали, как уменьшить размерность нашей матрицы признаков путем создания новых признаков с (в идеале) аналогичной способностью обучать качественные модели, но с значительно меньшей размерностью. Это называется извлечением признаков. В этой главе мы рассмотрим альтернативный подход: выбор высококачественных, информативных признаков и отбрасывание менее полезных признаков. Это называется выбором признаков.
Существует три типа методов выбора признаков: фильтр (filter), обертка (wrapper) и встроенный (embedded). Методы фильтра выбирают лучшие признаки, исследуя их статистические свойства. Методы, где мы явно устанавливаем порог для статистики или вручную выбираем количество признаков, которые хотим сохранить, являются примерами выбора признаков методом фильтрации. Методы обертки используют метод проб и ошибок для поиска подмножества признаков, которые дают модели наивысшего качества. Методы обертки часто являются наиболее эффективными, поскольку они находят лучший результат путем фактического экспериментирования в отличие от наивных предположений. Наконец, встроенные методы выбирают лучшее подмножество признаков как часть или расширение процесса обучения алгоритма.
В идеале, мы бы описали все три метода в этой главе. Однако, поскольку встроенные методы тесно связаны с конкретными алгоритмами обучения, их трудно объяснить до более глубокого погружения в сами алгоритмы. Поэтому в этой главе мы рассмотрим только методы выбора признаков методом фильтрации и обертки, оставив обсуждение конкретных встроенных методов до глав, где эти алгоритмы обучения будут обсуждаться подробно.
10.1 Пороговая обработка дисперсии числовых признаков
Проблема
У вас есть набор числовых признаков, и вы хотите отфильтровать те, у которых низкая дисперсия (т.е. вероятно, содержат мало информации).
Решение
Выберите подмножество признаков с дисперсией выше заданного порога:
# Load libraries
from sklearn.datasets import load_iris
from sklearn.feature_selection import VarianceThreshold
import some data to play with
iris = datasets.load_iris()
Create features and target
features = iris.data
target = iris.target
Create thresholder
thresholder = VarianceThreshold(threshold=.5)
Create high variance feature matrix
features_high_variance = thresholder.fit_transform(features)
View high variance feature matrix
features_high_variance[0:3]array([[ 5.1, 1.4, 0.2],
[ 4.9, 1.4, 0.2],
[ 4.7, 1.3, 0.2]])Обсуждение
Пороговая обработка дисперсии (VT) — это пример выбора признаков методом фильтрации, и один из самых базовых подходов к выбору признаков. Он мотивирован идеей, что признаки с низкой дисперсией, вероятно, менее интересны (и полезны), чем признаки с высокой дисперсией. VT сначала вычисляет дисперсию каждого признака:
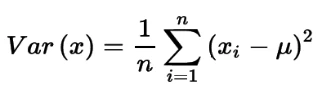
Рисунок: Формула дисперсии
где x — вектор признаков, xi — отдельное значение признака, а μ — среднее значение признака. Затем он отбрасывает все признаки, дисперсия которых не соответствует этому порогу.
При использовании VT следует учитывать две вещи. Во-первых, дисперсия не центрируется; то есть она находится в квадратичных единицах самого признака. Следовательно, VT не будет работать, когда наборы признаков содержат разные единицы измерения (например, один признак в годах, а другой в долларах). Во-вторых, порог дисперсии выбирается вручную, поэтому нам приходится использовать собственное суждение для выбора хорошего значения (или использовать метод выбора модели, описанный в [Ссылка на главу]). Мы можем увидеть дисперсию для каждого признака, используя variances_:
# View variances
thresholder.fit(features).variances_array([0.68112222, 0.18871289, 3.09550267, 0.57713289])Наконец, если признаки были стандартизированы (до нулевого среднего и единичной дисперсии), то по очевидным причинам пороговая обработка дисперсии не будет работать корректно:
# Load library
from sklearn.preprocessing import StandardScaler
Standardize feature matrix
scaler = StandardScaler()
features_std = scaler.fit_transform(features)
Caculate variance of each feature
selector = VarianceThreshold()
selector.fit(features_std).variances_array([1., 1., 1., 1.])10.2 Пороговая обработка дисперсии бинарных признаков
Проблема
У вас есть набор бинарных категориальных признаков, и вы хотите отфильтровать те, у которых низкая дисперсия (т.е. вероятно, содержат мало информации).
Решение
Выберите подмножество признаков с дисперсией случайной величины Бернулли выше заданного порога:
# Load library
from sklearn.feature_selection import VarianceThreshold
Create feature matrix with:
Feature 0: 80% class 0
Feature 1: 80% class 1
Feature 2: 60% class 0, 40% class 1
features = [[0, 1, 0],
[0, 1, 1],
[0, 1, 0],
[0, 1, 1],
[1, 0, 0]]
Run threshold by variance
thresholder = VarianceThreshold(threshold=(.75 * (1 - .75)))
thresholder.fit_transform(features)array([[0],
[1],
[0],
[1],
[0]])Обсуждение
Как и в случае с числовыми признаками, одна из стратегий выбора высокоинформативных категориальных признаков и отфильтровывания менее информативных — это анализ их дисперсии. В бинарных признаках (т.е. случайных величинах Бернулли) дисперсия вычисляется как:
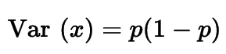
Рисунок: Формула дисперсии Бернулли
где p — доля наблюдений класса 1. Следовательно, установив p, мы можем удалить признаки, где подавляющее большинство наблюдений относится к одному классу.
10.3 Обработка сильно коррелированных признаков
Проблема
У вас есть матрица признаков, и вы подозреваете, что некоторые признаки сильно коррелированы.
Решение
Используйте матрицу корреляции для проверки сильно коррелированных признаков. Если сильно коррелированные признаки существуют, рассмотрите возможность удаления одного из коррелированных признаков:
# Load libraries
import pandas as pd
import numpy as np
Create feature matrix with two highly correlated features
features = np.array([[1, 1, 1],
[2, 2, 0],
[3, 3, 1],
[4, 4, 0],
[5, 5, 1],
[6, 6, 0],
[7, 7, 1],
[8, 7, 0],
[9, 7, 1]])
Convert feature matrix into DataFrame
dataframe = pd.DataFrame(features)
Create correlation matrix
corr_matrix = dataframe.corr().abs()
Select upper triangle of correlation matrix
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape),
k=1).astype(bool))
Find index of feature columns with correlation greater than 0.95
to_drop = [column for column in upper.columns if any(upper[column] > 0.95)]
Drop features
dataframe.drop(dataframe.columns[to_drop], axis=1).head(3)| 0 | 2 | |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 2 | 0 |
| 2 | 3 | 1 |
Обсуждение
Одна проблема, с которой мы часто сталкиваемся в машинном обучении, — это сильно коррелированные признаки. Если два признака сильно коррелированы, то информация, которую они содержат, очень похожа, и, вероятно, избыточно включать оба признака. В случае простых моделей, таких как линейная регрессия, неспособность удалить такие признаки нарушает предположения линейной регрессии и может привести к искусственно завышенному значению R-квадрата. Решение проблемы сильно коррелированных признаков простое: удалить один из них из набора признаков. Удаление сильно коррелированных признаков способом, описанным выше, — еще один пример фильтрации.
В нашем решении сначала мы создаем матрицу корреляции всех признаков:
# Correlation matrix
dataframe.corr()| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.000000 | 0.976103 | 0.000000 |
| 1 | 0.976103 | 1.000000 | -0.034503 |
| 2 | 0.000000 | -0.034503 | 1.000000 |
Во-вторых, мы рассматриваем верхний треугольник матрицы корреляции для идентификации пар сильно коррелированных признаков:
# Upper triangle of correlation matrix
upper| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | NaN | 0.976103 | 0.000000 |
| 1 | NaN | NaN | 0.034503 |
| 2 | NaN | NaN | NaN |
В-третьих, мы удаляем один признак из каждой из этих пар из набора признаков.
10.4 Удаление нерелевантных признаков для классификации
Проблема
У вас есть категориальный целевой вектор, и вы хотите удалить неинформативные признаки.
Решение
Если признаки категориальные, вычислите статистику хи-квадрат (χ2) между каждым признаком и целевым вектором:
# Load libraries
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2, f_classif
Load data
iris = load_iris()
features = iris.data
target = iris.target
Convert to categorical data by converting data to integers
features = features.astype(int)
Select two features with highest chi-squared statistics
chi2_selector = SelectKBest(chi2, k=2)
features_kbest = chi2_selector.fit_transform(features, target)
Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])Original number of features: 4
Reduced number of features: 2Если признаки количественные, вычислите F-критерий ANOVA между каждым признаком и целевым вектором:
# Select two features with highest F-values
fvalue_selector = SelectKBest(f_classif, k=2)
features_kbest = fvalue_selector.fit_transform(features, target)
Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])Original number of features: 4
Reduced number of features: 2Вместо выбора определенного количества признаков мы также можем использовать SelectPercentile для выбора верхних n процентов признаков:
# Load library
from sklearn.feature_selection import SelectPercentile
Select top 75% of features with highest F-values
fvalue_selector = SelectPercentile(f_classif, percentile=75)
features_kbest = fvalue_selector.fit_transform(features, target)
Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kbest.shape[1])Original number of features: 4
Reduced number of features: 3Обсуждение
Статистика хи-квадрат исследует независимость двух категориальных векторов. То есть статистика представляет собой разницу между наблюдаемым количеством наблюдений в каждом классе категориального признака и тем, что мы ожидали бы, если бы этот признак был независимым (т.е. не было бы связи) с целевым вектором:
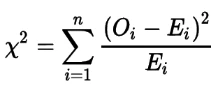
Рисунок: Формула хи-квадрат
где Oi — количество наблюдений в классе i, а Ei — количество наблюдений в классе i, которые мы теоретически ожидали бы, если бы не было связи между признаком и целевым вектором.
Статистика хи-квадрат — это одно число, которое сообщает вам, насколько велика разница между вашими наблюдаемыми количествами и количествами, которые вы ожидали бы, если бы в популяции не было вообще никакой связи. Вычисляя статистику хи-квадрат между признаком и целевым вектором, мы получаем меру независимости между ними. Если целевая переменная не зависит от переменной признака, то она нерелевантна для наших целей, потому что она не содержит информации, которую мы можем использовать для классификации. С другой стороны, если два признака сильно зависят друг от друга, они, вероятно, очень информативны для обучения нашей модели.
Чтобы использовать хи-квадрат при выборе признаков, мы вычисляем статистику хи-квадрат между каждым признаком и целевым вектором, затем выбираем признаки с наилучшими статистиками хи-квадрат. В scikit-learn мы можем использовать SelectKBest для выбора признаков с наилучшими статистиками. Параметр k определяет количество признаков, которые мы хотим сохранить, и отфильтровывает наименее информативные признаки.
Важно отметить, что статистика хи-квадрат может быть вычислена только между двумя категориальными векторами. По этой причине хи-квадрат для выбора признаков требует, чтобы как целевой вектор, так и признаки были категориальными. Однако, если у нас есть числовой признак, мы можем использовать технику хи-квадрат, сначала преобразовав количественный признак в категориальный. Наконец, чтобы использовать наш подход хи-квадрат, все значения должны быть неотрицательными.
Альтернативно, если у нас есть числовой признак, мы можем использовать f_classif для вычисления статистики F-критерия ANOVA между каждым признаком и целевым вектором. Оценки F-критерия исследуют, являются ли средние значения для каждой группы статистически значимо разными, когда мы группируем числовой признак по целевому вектору. Например, если бы у нас был бинарный целевой вектор (пол) и количественный признак (баллы теста), F-критерий показал бы нам, отличается ли средний балл теста для мужчин от среднего балла теста для женщин. Если нет, то балл теста не помогает нам предсказывать пол, и, следовательно, признак нерелевантен.
10.5 Рекурсивное исключение признаков
Проблема
Вы хотите автоматически выбрать лучшие признаки для сохранения.
Решение
Используйте RFECV scikit-learn для проведения рекурсивного исключения признаков (RFE) с использованием кросс-валидации (CV). То есть используйте метод выбора признаков обертки и многократно обучайте модель, каждый раз удаляя признак, пока производительность модели (например, точность) не ухудшится. Оставшиеся признаки являются лучшими:
# Load libraries
import warnings
from sklearn.datasets import make_regression
from sklearn.feature_selection import RFECV
from sklearn import datasets, linear_model
Suppress an annoying but harmless warning
warnings.filterwarnings(action="ignore", module="scipy",
message="^internal gelsd")
Generate features matrix, target vector, and the true coefficients
features, target = make_regression(n_samples = 10000,
n_features = 100,
n_informative = 2,
random_state = 1)
Create a linear regression
ols = linear_model.LinearRegression()
Recursively eliminate features
rfecv = RFECV(estimator=ols, step=1, scoring="neg_mean_squared_error")
rfecv.fit(features, target)
rfecv.transform(features)array([[ 0.00850799, 0.7031277 , 1.52821875],
[-1.07500204, 2.56148527, -0.44567768],
[ 1.37940721, -1.77039484, -0.74675125],
...,
[-0.80331656, -1.60648007, 0.52231601],
[ 0.39508844, -1.34564911, 0.4228057 ],
[-0.55383035, 0.82880112, 1.73232647]])После проведения RFE мы можем увидеть количество признаков, которые мы должны оставить:
# Number of best features
rfecv.n_features_3Мы также можем увидеть, какие из этих признаков мы должны оставить:
# Which categories are best
rfecv.support_array([False, False, False, False, False, True, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, True, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, True, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False])Мы даже можем просмотреть рейтинги признаков:
# Rank features best (1) to worst
rfecv.ranking_array([11, 92, 96, 87, 46, 1, 48, 23, 16, 2, 66, 83, 33, 27, 70, 75, 29,
84, 54, 88, 37, 42, 85, 62, 74, 50, 80, 10, 38, 59, 79, 57, 44, 8,
82, 45, 89, 69, 94, 1, 35, 47, 39, 1, 34, 72, 19, 4, 17, 91, 90,
24, 32, 13, 49, 26, 12, 71, 68, 40, 1, 43, 63, 28, 73, 58, 21, 67,
1, 95, 77, 93, 22, 52, 30, 60, 81, 14, 86, 18, 15, 41, 7, 53, 65,
51, 64, 6, 9, 20, 5, 55, 56, 25, 36, 61, 78, 31, 3, 76])Обсуждение
Это, вероятно, самый сложный рецепт в этой книге на данный момент, объединяющий ряд тем, которые мы еще не рассмотрели подробно. Однако интуиция достаточно проста, чтобы мы могли рассмотреть ее здесь, а не откладывать до более поздней главы. Идея RFE заключается в многократном обучении модели, обновляя веса или коэффициенты этой модели каждый раз. При первом обучении модели мы включаем все признаки. Затем мы находим признак с наименьшим параметром (обратите внимание, что это предполагает, что признаки масштабированы или стандартизированы), что означает, что он менее важен, и удаляем признак из набора признаков.
Тогда возникает очевидный вопрос: сколько признаков нам следует оставить? Мы можем (гипотетически) повторять этот цикл, пока у нас не останется только один признак. Лучший подход требует включения нового концепта, называемого кросс-валидацией (CV). Мы обсудим кросс-валидацию подробно в следующей главе, но вот общая идея.
Имея данные, содержащие 1) целевую переменную, которую мы хотим предсказать, и 2) матрицу признаков, мы сначала разбиваем данные на две группы: обучающую выборку и тестовую выборку. Во-вторых, мы обучаем нашу модель, используя обучающую выборку. В-третьих, мы делаем вид, что не знаем целевую переменную тестовой выборки, и применяем нашу модель к признакам тестовой выборки, чтобы предсказать значения тестовой выборки. Наконец, мы сравниваем предсказанные значения целевой переменной с истинными значениями целевой переменной, чтобы оценить нашу модель.
Мы можем использовать CV для поиска оптимального количества признаков для сохранения во время RFE. В частности, в RFE с CV после каждой итерации мы используем кросс-валидацию для оценки нашей модели. Если CV показывает, что наша модель улучшилась после удаления признака, то мы продолжаем следующий цикл. Однако, если CV показывает, что наша модель ухудшилась после удаления признака, мы возвращаем этот признак в набор признаков и выбираем эти признаки как лучшие.
В scikit-learn RFE с CV реализован с использованием RFECV и содержит ряд важных параметров. Параметр estimator определяет тип модели, которую мы хотим обучить (например, линейная регрессия). Параметр step устанавливает количество или долю признаков, которые нужно удалить в каждом цикле. Параметр scoring устанавливает метрику качества, которую мы используем для оценки нашей модели во время кросс-валидации.
См. также
Recursive feature elimination with cross-validation
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- 100 Страниц о машинном обучении
- Математика для нейронного обучения