Глава 9. Уменьшение размерности с использованием извлечения признаков
9.0 Введение
Часто приходится иметь дело с тысячами и даже сотнями тысяч признаков. Например, в Главе 8 мы преобразовали цветное изображение размером 256 × 256 пикселей в 196 608 признаков. Более того, поскольку каждый из этих пикселей может принимать одно из 256 возможных значений, существует 256196608 различных конфигураций, которые может принять наше наблюдение. Многие алгоритмы машинного обучения испытывают трудности с обучением на таких данных, потому что мы практически никогда не сможем собрать достаточно наблюдений, чтобы алгоритмы работали корректно. Даже в более табличных, структурированных наборах данных мы можем легко получить тысячи признаков после процесса инженерии признаков.
К счастью, не все признаки созданы равными, и цель извлечения признаков для уменьшения размерности состоит в преобразовании нашего набора признаков, poriginal, таким образом, чтобы мы получили новый набор, pnew, где poriginal > pnew, при этом сохраняя большую часть базовой информации. Иными словами, мы уменьшаем количество признаков с небольшой потерей способности наших данных генерировать высококачественные предсказания. В этой главе мы рассмотрим ряд методов извлечения признаков, чтобы сделать именно это.
Одним из недостатков методов извлечения признаков, которые мы обсуждаем, является то, что новые признаки, которые мы генерируем, не будут интерпретируемы человеком. Они будут содержать столько же или почти столько же способности для обучения наших моделей, но будут выглядеть для человеческого глаза как набор случайных чисел. Если мы хотим сохранить нашу способность интерпретировать наши модели, уменьшение размерности с помощью выбора признаков является лучшим вариантом.
9.1 Уменьшение количества признаков с использованием главных компонент
Проблема
Имея набор признаков, вы хотите уменьшить их количество, сохраняя при этом дисперсию (важную информацию) в данных.
Решение
Используйте анализ главных компонент с помощью PCA scikit:
# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
Load the data
digits = datasets.load_digits()
Standardize the feature matrix
features = StandardScaler().fit_transform(digits.data)
Create a PCA that will retain 99% of variance
pca = PCA(n_components=0.99, whiten=True)
Conduct PCA
features_pca = pca.fit_transform(features)
Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_pca.shape[1])Original number of features: 64
Reduced number of features: 54Обсуждение
Анализ главных компонент (PCA) — популярная техника уменьшения размерности. PCA проецирует наблюдения на (надеюсь, меньшее количество) главных компонент матрицы признаков, которые сохраняют наибольшую дисперсию в данных — что практически означает, что мы сохраняем информацию. PCA — это метод обучения без учителя, что означает, что он не использует информацию из целевого вектора, а вместо этого рассматривает только матрицу признаков.
Для математического описания принципов работы PCA см. внешние ресурсы, перечисленные в конце этого рецепта. Однако мы можем понять интуицию, лежащую в основе PCA, используя простой пример. На следующем рисунке наши данные содержат два признака, x1 и x2. Глядя на визуализацию, должно быть ясно, что наблюдения разбросаны как сигара, с большой длиной и очень небольшой высотой. Более конкретно, мы можем сказать, что дисперсия «длины» значительно больше, чем «высоты». Вместо длины и высоты мы используем «направления» с наибольшей дисперсией в качестве первой главной компоненты и «направление» со второй по величине дисперсией в качестве второй главной компоненты (и так далее).
Если бы мы хотели уменьшить количество наших признаков, одной из стратегий было бы проецирование всех наблюдений в нашем 2D пространстве на 1D главную компоненту. Мы бы потеряли информацию, захваченную во второй главной компоненте, но в некоторых ситуациях это был бы приемлемый компромисс. Это и есть PCA.
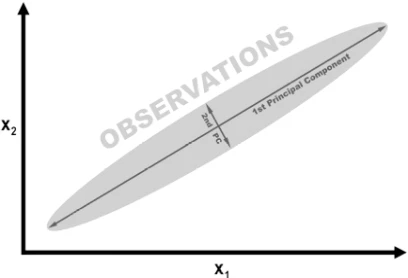
Рисунок 1
PCA реализован в scikit-learn с использованием класса PCA. n_components имеет два режима работы, зависящие от предоставленного аргумента. Если аргумент больше 1, n_components вернет столько признаков. Это приводит к вопросу о том, как выбрать оптимальное количество признаков. К счастью для нас, если аргумент n_components находится в диапазоне от 0 до 1, pca возвращает минимальное количество признаков, которое сохраняет такую долю дисперсии. Часто используются значения 0.95 и 0.99, что означает, что сохранены 95% и 99% дисперсии исходных признаков соответственно. whiten=True преобразует значения каждой главной компоненты так, чтобы они имели нулевое среднее и единичную дисперсию. Другой параметр и аргумент — svd_solver="randomized", который реализует стохастический алгоритм для нахождения первых главных компонент за значительно меньшее время.
Вывод нашего решения показывает, что PCA позволил нам уменьшить размерность на 10 признаков, при этом сохранив 99% информации (дисперсии) в матрице признаков.
См. также
scikit-learn documentation on PCA
Choosing the Number of Principal Components
Principal component analysis with linear algebra
9.2 Уменьшение количества признаков при линейно неразделимых данных
Проблема
Вы подозреваете, что у вас линейно неразделимые данные, и хотите уменьшить размерность.
Решение
Используйте расширение анализа главных компонент, которое использует ядра для нелинейного уменьшения размерности:
# Load libraries
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
Create linearly inseparable data
features, _ = make_circles(n_samples=1000, random_state=1, noise=0.1, factor=0.1)
Apply kernal PCA with radius basis function (RBF) kernel
kpca = KernelPCA(kernel="rbf", gamma=15, n_components=1)
features_kpca = kpca.fit_transform(features)
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kpca.shape[1])Original number of features: 2
Reduced number of features: 1Обсуждение
PCA способен уменьшать размерность нашей матрицы признаков (например, количество признаков). Стандартный PCA использует линейную проекцию для уменьшения количества признаков. Если данные линейно разделимы (т.е. вы можете провести прямую линию или гиперплоскость между разными классами), то PCA работает хорошо. Однако, если ваши данные не линейно разделимы (т.е. вы можете разделить классы только с помощью криволинейной границы принятия решений), линейное преобразование не будет работать хорошо. В нашем решении мы использовали make_circles scikit-learn для генерации смоделированного набора данных с целевым вектором из двух классов и двух признаков. make_circles создает линейно неразделимые данные; в частности, один класс окружен со всех сторон другим классом.
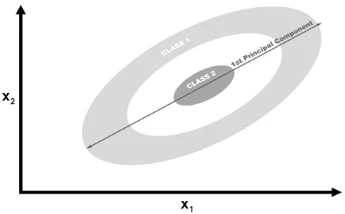
Рисунок 2
Рисунок 2: Первая главная компонента, спроецированная на линейно неразделимые данные
Если бы мы использовали линейный PCA для уменьшения размерности наших данных, два класса были бы линейно спроецированы на первую главную компоненту таким образом, что они переплелись бы.

Рисунок 3
Рисунок 3: Первая главная компонента линейно неразделимых данных без ядерного PCA
В идеале, мы хотели бы преобразование, которое как уменьшило бы размерность, так и сделало данные линейно разделимыми. Ядерный PCA может сделать и то, и другое.

Рисунок 4
Рисунок 4: Первая главная компонента линейно неразделимых данных с ядерным PCA
Ядра позволяют нам проецировать линейно неразделимые данные в более высокую размерность, где они становятся линейно разделимыми; это называется трюком с ядром (kernel trick). Не беспокойтесь, если вы не понимаете деталей трюка с ядром; просто считайте ядра разными способами проецирования данных. В scikit-learn есть ряд ядер, которые мы можем использовать в классе kernelPCA, указанных с помощью параметра kernel. Общее ядро для использования — это ядро радиальной базисной функции Гаусса rbf, но другие варианты — полиномиальное ядро (poly) и сигмоидное ядро (sigmoid). Мы можем даже указать линейную проекцию (linear), которая даст те же результаты, что и стандартный PCA.
Одним из недостатков ядерного PCA является то, что нам нужно указать ряд параметров. Например, в Рецепте 9.1 мы установили n_components равным 0.99, чтобы PCA выбрал количество компонент, сохраняющих 99% дисперсии. У нас нет этой опции в ядерном PCA. Вместо этого мы должны определить количество компонент (например, n_components=1). Кроме того, ядра имеют свои собственные гиперпараметры, которые нам придется установить; например, радиальная базисная функция требует значения gamma.
Итак, как мы узнаем, какие значения использовать? Методом проб и ошибок. В частности, мы можем обучать нашу модель машинного обучения несколько раз, каждый раз с другим ядром или другим значением параметра. После того как мы найдем комбинацию значений, которая дает предсказанные значения самого высокого качества, мы завершили. Это общая тема в машинном обучении, и мы подробно изучим эту стратегию в [Ссылка на главу].
См. также
scikit-learn documentation on Kernel PCA
Kernel tricks and nonlinear dimensionality reduction via RBF kernel PCA
9.3 Уменьшение количества признаков путем максимизации разделимости классов
Проблема
Вы хотите уменьшить количество признаков, используемых классификатором, путем максимизации разделения между классами.
Решение
Попробуйте линейный дискриминантный анализ (LDA) для проецирования признаков на оси компонент, которые максимизируют разделение классов:
# Load libraries
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
Load Iris flower dataset:
iris = datasets.load_iris()
features = iris.data
target = iris.target
Create and run an LDA, then use it to transform the features
lda = LinearDiscriminantAnalysis(n_components=1)
features_lda = lda.fit(features, target).transform(features)
Print the number of features
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_lda.shape[1])Original number of features: 4
Reduced number of features: 1Мы можем использовать explained_variance_ratio_ для просмотра доли дисперсии, объясняемой каждой компонентой. В нашем решении одна компонента объяснила более 99% дисперсии:
lda.explained_variance_ratio_array([0.9912126])Обсуждение
LDA — это классификация, которая также является популярной техникой уменьшения размерности. LDA работает аналогично анализу главных компонент (PCA) тем, что проецирует наше пространство признаков на пространство меньшей размерности. Однако, в PCA нас интересовали только оси компонент, которые максимизируют дисперсию в данных, тогда как в LDA у нас есть дополнительная цель — максимизация различий между классами. В этом примере на картинке у нас есть данные, содержащие два целевых класса и два признака. Если мы спроецируем данные на ось y, два класса не будут легко разделимы (т.е. они перекрываются), в то время как если мы спроецируем данные на ось x, мы получим вектор признаков (т.е. мы уменьшили размерность на единицу), который все еще сохраняет разделимость классов. В реальном мире, конечно, взаимосвязь между классами будет более сложной, а размерность будет выше, но концепция остается прежней.
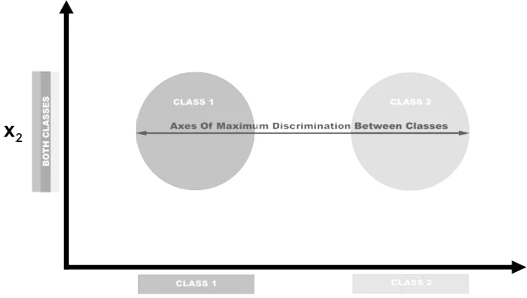
Рисунок 5
В scikit-learn LDA реализован с использованием LinearDiscriminantAnalysis, который включает параметр n_components, указывающий количество признаков, которые мы хотим получить в результате. Чтобы выяснить, какое значение аргумента использовать с n_components (например, сколько параметров сохранить), мы можем воспользоваться тем фактом, что explained_variance_ratio_ сообщает нам дисперсию, объясняемую каждым выходным признаком, и является отсортированным массивом. Например:
lda.explained_variance_ratio_array([0.9912126])В частности, мы можем запустить LinearDiscriminantAnalysis с n_components равным None, чтобы получить отношение дисперсии, объясняемой каждым признаком компоненты, а затем вычислить, сколько компонент требуется, чтобы получить значение выше некоторого порога объясненной дисперсии (часто 0.95 или 0.99):
# Create and run LDA
lda = LinearDiscriminantAnalysis(n_components=None)
features_lda = lda.fit(features, target)
Create array of explained variance ratios
lda_var_ratios = lda.explained_variance_ratio_
Create function
def select_n_components(var_ratio, goal_var: float) -> int:
Set initial variance explained so far
total_variance = 0.0
Set initial number of features
n_components = 0
For the explained variance of each feature:
for explained_variance in var_ratio:
Add the explained variance to the total
total_variance += explained_variance
Add one to the number of components
n_components += 1
If we reach our goal level of explained variance
if total_variance >= goal_var:
End the loop
break
Return the number of components
return n_components
Run function
select_n_components(lda_var_ratios, 0.95)1См. также
Comparison of LDA and PCA 2D projection of Iris dataset
Linear Discriminant Analysis
9.4 Уменьшение количества признаков с использованием матричной факторизации
Проблема
У вас есть матрица признаков с неотрицательными значениями, и вы хотите уменьшить размерность.
Решение
Используйте неотрицательную матричную факторизацию (NMF) для уменьшения размерности матрицы признаков:
# Load libraries
from sklearn.decomposition import NMF
from sklearn import datasets
Load the data
digits = datasets.load_digits()
Load feature matrix
features = digits.data
Create, fit, and apply NMF
nmf = NMF(n_components=10, random_state=4)
features_nmf = nmf.fit_transform(features)
Show results
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_nmf.shape[1])Original number of features: 64
Reduced number of features: 10Обсуждение
NMF — это метод обучения без учителя для линейного уменьшения размерности, который факторизует (т.е. разбивает на несколько матриц, произведение которых аппроксимирует исходную матрицу) матрицу признаков на матрицы, представляющие скрытую связь между наблюдениями и их признаками. Интуитивно, NMF может уменьшить размерность, потому что при умножении матриц два фактора (умножаемые матрицы) могут иметь значительно меньше измерений, чем результирующая матрица. Формально, при заданном желаемом количестве возвращаемых признаков, r, NMF факторизует нашу матрицу признаков таким образом, что:
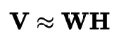
Рисунок: Формула NMF
где V — наша матрица признаков n × d (т.е. d признаков, n наблюдений), W — n × r, а H — r × d матрица. Настраивая значение r, мы можем установить желаемое количество уменьшения размерности.
Основное требование NMA заключается в том, что, как следует из названия, матрица признаков не может содержать отрицательных значений. Кроме того, в отличие от PCA и других рассмотренных нами техник, NMA не предоставляет нам объясненную дисперсию выходных признаков. Таким образом, лучший способ найти оптимальное значение n_components — это перебирать диапазон значений, чтобы найти то, которое дает наилучший результат в нашей конечной модели (см. [Ссылка на главу]).
См. также
Non-Negative Matrix Factorization (NMF)
9.5 Уменьшение количества признаков на разреженных данных
Проблема
У вас есть разреженная матрица признаков, и вы хотите уменьшить размерность.
Решение
Используйте Truncated Singular Value Decomposition (TSVD):
# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
from sklearn import datasets
import numpy as np
Load the data
digits = datasets.load_digits()
Standardize feature matrix
features = StandardScaler().fit_transform(digits.data)
Make sparse matrix
features_sparse = csr_matrix(features)
Create a TSVD
tsvd = TruncatedSVD(n_components=10)
Conduct TSVD on sparse matrix
features_sparse_tsvd = tsvd.fit(features_sparse).transform(features_sparse)
Show results
print("Original number of features:", features_sparse.shape[1])
print("Reduced number of features:", features_sparse_tsvd.shape[1])Original number of features: 64
Reduced number of features: 10Обсуждение
TSVD аналогичен PCA и, по сути, PCA часто использует неотсеченное сингулярное разложение (SVD) на одном из своих шагов. В обычном SVD, при наличии d признаков, SVD создает факторные матрицы размером d × d, тогда как TSVD возвращает факторы размером n × n, где n ранее указывалось параметром. Практическое преимущество TSVD заключается в том, что, в отличие от PCA, он работает с разреженными матрицами признаков.
Одна проблема с TSVD заключается в том, что из-за использования генератора случайных чисел знаки вывода могут меняться между подгонками. Простой обходной путь — использовать fit только один раз для всего конвейера предварительной обработки, а затем многократно использовать transform.
Как и в случае с линейным дискриминантным анализом, нам нужно указать количество признаков (компонент), которые мы хотим получить. Это делается с помощью параметра n_components. Естественный вопрос: какое оптимальное количество компонент? Одна из стратегий — включить n_components в качестве гиперпараметра для оптимизации во время выбора модели (т.е. выбрать значение для n_components, которое дает наилучшую обученную модель). Альтернативно, поскольку TSVD предоставляет нам отношение дисперсии исходной матрицы признаков, объясняемой каждой компонентой, мы можем выбрать количество компонент, которые объясняют желаемую долю дисперсии (95% или 99% — распространенные значения). Например, в нашем решении первые три выходные компоненты объясняют приблизительно 30% дисперсии исходных данных:
# Sum of first three components' explained variance ratios
tsvd.explained_variance_ratio_[0:3].sum()0.3003938537287226Мы можем автоматизировать процесс, создав функцию, которая запускает TSVD с n_components, установленным на единицу меньше, чем количество исходных признаков, а затем вычисляет количество компонент, которые объясняют желаемую долю дисперсии исходных данных:
# Create and run an TSVD with one less than number of features
tsvd = TruncatedSVD(n_components=features_sparse.shape[1]-1)
features_tsvd = tsvd.fit(features)
List of explained variances
tsvd_var_ratios = tsvd.explained_variance_ratio_
Create a function
def select_n_components(var_ratio, goal_var):
Set initial variance explained so far
total_variance = 0.0
Set initial number of features
n_components = 0
For the explained variance of each feature:
for explained_variance in var_ratio:
Add the explained variance to the total
total_variance += explained_variance
Add one to the number of components
n_components += 1
If we reach our goal level of explained variance
if total_variance >= goal_var:
End the loop
break
Return the number of components
return n_components
Run function
select_n_components(tsvd_var_ratios, 0.95)40См. также
scikit-learn documentation TruncatedSVD
Другие статьи по этой теме:
- Маленькая книга о глубоком обучении
- 100 Страниц о машинном обучении
- Математика для нейронного обучения